Критичні точки функції інтервали зростання спадання онлайн. Зростання та зменшення функцій, екстремуми

Зростання та зменшення функції

функція y = f(x) називається зростаючою на відрізку [ a, b], якщо для будь-якої пари точок хі х", а ≤ х виконується нерівність f(x) ≤ f (x"), і строго зростаючою - якщо виконується нерівність f (x) f(x"). Аналогічно визначається спадання та суворе зменшення функції. Наприклад, функція у = х 2 (Рис. , а) строго зростає на відрізку , а

(Рис. б) суворо зменшується на цьому відрізку. Зростаючі функції позначаються f (x), а спадні f (x)↓. Для того щоб диференційована функція f (x) була зростаючою на відрізку [ а, b], необхідно і достатньо, щоб її похідна f"(x) була невід'ємною на [ а, b].

Поряд із зростанням і зменшенням функції на відрізку розглядають зростання і зменшення функції в точці. Функція у = f (x) називається зростаючою в точці x 0 якщо знайдеться такий інтервал (α, β), що містить точку x 0 , що для будь-якої точки хз (α, β), х> x 0 , виконується нерівність f (x 0) ≤ f (x), і для будь-якої точки хз (α, β), х 0 виконується нерівність f (x) ≤ f (x 0). Аналогічно визначається строге зростання функції у точці x 0 . Якщо f"(x 0) > 0, то функція f(x) строго зростає в точці x 0 . Якщо f (x) зростає в кожній точці інтервалу ( a, b), вона зростає у цьому інтервалі.

С. Б. Стєчкін.

Велика радянська енциклопедія. - М: Радянська енциклопедія. 1969-1978 .

Дивитися що таке "Зростання та зменшення функції" в інших словниках:

Поняття математичного аналізу. Функція f(x) називається зростаючою на відрізку ВІКОВА СТРУКТУРА НАСЕЛЕННЯ співвідношення чисельності різних вікових груп населення. Залежить від рівнів народжуваності та смертності, тривалості життя людей. Великий Енциклопедичний словник

Поняття математичного аналізу. Функція f(х) називається зростаючою на відрізку якщо для будь-якої пари точок x1 і x2, a≤x1 … Енциклопедичний словник

Концепція матем. аналізу. Фція f(x) зв. зростаючою на відрізку [а, b], якщо для будь-якої пари точок х1 та x2, а<или=х1 <х<или=b, выполняется неравенство f(x1)Природознавство. Енциклопедичний словник

Розділ математики, в якому вивчаються похідні та диференціали функцій та їх застосування до дослідження функцій. Оформлення Д. в. у самостійну математичну дисципліну пов'язано з іменами І. Ньютона та Г. Лейбніца (друга половина 17 … Велика Радянська Енциклопедія

Розділ математики, в якому вивчаються поняття похідної та диференціала і способи їх застосування до дослідження функцій. Розвиток Д. в. тісно пов'язані з розвитком інтегрального обчислення. Нерозривно та його зміст. Разом вони становлять основу. Математична енциклопедія

Цей термін має й інші значення, див. функція. Запит «Відображення» перенаправляється сюди; див. також інші значення … Вікіпедія

Аристотель та перипатетики- Арістотелівське питання Життя Арістотеля Арістотель народився в 384/383 гг. до зв. е. у Стагірі, на кордоні з Македонією. Його батько на ім'я Нікомах був лікарем на службі у македонського царя Амінта, отця Пилипа. Разом із сім'єю молодий Арістотель… Західна філософія від витоків до наших днів

- (КХД), квантовопольова теорія сильної дії кварків і глюонів, побудована за образом квант. електродинаміки (КЕД) на основі «колірної» калібрувальної симетрії На відміну від КЕД, ферміони у КХД мають доповнити. ступінь свободи квант. число,… … Фізична енциклопедія

I Серце Серце (лат. соr, грец. cardia) порожнистий фіброзно-м'язовий орган, який, функціонуючи як насос, забезпечує рух крові а системі кровообігу. Анатомія Серце знаходиться у передньому середостінні (Середостіння) у Перікарді між… Медична енциклопедія

Життя рослини, як і будь-якого іншого живого організму, є складною сукупністю взаємопов'язаних процесів; найбільш істотний їх, як відомо, обмін речовин із довкіллям. Середовище є джерелом, звідки… … Біологічна енциклопедія

Щоб визначити характер функції та говорити про її поведінку, необхідно знаходити проміжки зростання та спадання. Цей процес отримав назву дослідження функції та побудови графіка. Точка екстремуму використовується при знаходженні найбільшого та найменшого значення функції, тому що в них відбувається зростання або зменшення функції з інтервалу.

Ця стаття розкриває визначення, формулюємо достатня ознаказростання та спадання на інтервалі та умова існування екстремуму. Це можна застосувати до вирішення прикладів і завдань. Потрібно повторити розділ диференціювання функцій, тому що при вирішенні необхідно використовувати знаходження похідної.

Yandex.RTB R-A-339285-1 Визначення 1

Функція y = f (x) зростатиме на інтервалі x , коли за будь-яких x 1 ∈ X і x 2 ∈ X , x 2 > x 1 нерівність f (x 2) > f (x 1) буде здійсненною. Інакше висловлюючись, більшому значенню аргументу відповідає більше значення функції.

Визначення 2

Функція y = f (x) вважається спадною на інтервалі x , коли за будь-яких x 1 ∈ X , x 2 ∈ X , x 2 > x 1 рівність f (x 2) > f (x 1) вважається здійсненним. Інакше висловлюючись, більшого значення функції відповідає менше значення аргументу. Розглянемо малюнок, наведений нижче.

Примітка: Коли функція певна і безперервна в кінцях інтервалу зростання і спадання, тобто (a; b) , де х = а, х = b точки включені в проміжок зростання і спадання. Визначенню це суперечить, отже, має місце на проміжку x .

Основні властивості елементарних функцій типу y = sin x – визначеність та безперервність при дійсних значеннях аргументів. Звідси отримуємо, що зростання синуса відбувається на інтервалі - π 2; π 2, тоді зростання на відрізку має вигляд - π 2; π 2 .

Крапка х 0 називається точкою максимумудля функції y = f (x) , коли для всіх значень x нерівність f (x 0) ≥ f (x) справедлива. Максимум функції– це значення функції у точці, причому позначається y m a x .

Точка х 0 називається точкою мінімуму функції y = f (x) , коли всім значень x нерівність f (x 0) ≤ f (x) є справедливим. Мінімум функції– це значення функції у точці, причому має позначення виду y m i n .

Околицями точки х 0 вважаються точки екстремуму,а значення функції, що відповідає точкам екстремуму. Розглянемо малюнок, наведений нижче.

Екстремуми функції з найбільшим та з найменшим значеннямфункції. Розглянемо малюнок, наведений нижче.

Перший малюнок говорить про те, що потрібно знайти найбільше значенняфункції з відрізка [a; b]. Воно знаходиться за допомогою точок максимуму і дорівнює максимальному значенню функції, а другий малюнок більше схожий на пошук точки максимуму при х = b.

Достатні умови зростання та зменшення функції

Щоб знайти максимуми та мінімуми функції, необхідно застосовувати ознаки екстремуму у разі, коли функція задовольняє цим умовам. Найчастіше використовуваним вважається перша ознака.

Перша достатня умова екстремуму

Нехай задана функція y = f (x) , яка диференційована в околиці точки x 0 , причому має безперервність в заданій точці x 0 . Звідси отримуємо, що

• коли f "(x) > 0 з x ∈ (x 0 - ε; x 0) і f "(x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• коли f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 при x ∈ (x 0 ; x 0 + ε) тоді x 0 є точкою мінімуму.

Інакше кажучи, отримаємо їх умови встановлення знака:

• коли функція безперервна в точці x 0 тоді має похідну з змінним знаком, тобто з + на - , Отже, точка називається максимумом;
• коли функція безперервна в точці x 0 тоді має похідну з змінним знаком з - на + , значить, точка називається мінімумом.

Щоб правильно визначити точки максимуму та мінімуму функції, необхідно слідувати алгоритму їх знаходження:

• знайти область визначення;
• знайти похідну функції у цій галузі;
• визначити нулі та точки, де функція не існує;
• визначення знака похідної на інтервалах;
• вибрати точки, де функція змінює знак.

Розглянемо алгоритм з прикладу рішення кількох прикладів перебування екстремумів функції.

Приклад 1

Знайти точки максимуму та мінімуму заданої функції y = 2 (x + 1) 2 x – 2 .

Рішення

Область визначення цієї функції – це дійсні числа крім х = 2 . Для початку знайдемо похідну функції та отримаємо:

y " = 2 x + 1 2 x - 2 " = 2 · x + 1 2 " · (x - 2) - (x + 1) 2 · (x - 2) "(x - 2) 2 = = 2 · 2 · (x + 1) · (x + 1) " · (x - 2) - (x + 1) 2 · 1 (x - 2) 2 = 2 · 2 · (x + 1) · (x - 2) ) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Звідси бачимо, що нулі функції - це х = - 1, х = 5, х = 2, тобто кожну дужку необхідно прирівняти до нуля. Зазначимо на числовій осі та отримаємо:

Тепер визначимо знаки похідної кожного інтервалу. Необхідно вибрати точку, що входить в інтервал, підставити у вираз. Наприклад, точки х = - 2, х = 0, х = 3, х = 6.

Отримуємо, що

y "(-2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0 , отже, інтервал - ∞ , - 1 має позитивну похідну.

y "(0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Оскільки другий інтервал вийшов меншим за нуль, значить, похідна на відрізку буде негативною. Третій із мінусом, четвертий із плюсом. Для визначення безперервності необхідно звернути увагу на похідний знак, якщо він змінюється, тоді це точка екстремуму.

Отримаємо, що у точці х = - 1 функція буде безперервна, отже похідна змінить знак з + на - . За першою ознакою маємо, що х = - 1 є точкою максимуму, отже отримуємо

y m a x = y (-1) = 2 · (x + 1) 2 x - 2 x = - 1 = 2 · (- 1 + 1) 2 - 1 - 2 = 0

Точка х = 5 свідчить про те, що функція є безперервною, а похідна змінить знак з – на +. Отже, х=-1 є точкою мінімуму, причому її знаходження має вигляд

y m i n = y (5) = 2 · (x + 1) 2 x - 2 x = 5 = 2 · (5 + 1) 2 5 - 2 = 24

Графічне зображення

Відповідь: y m a x = y (-1) = 0, y m i n = y (5) = 24 .

Варто звернути увагу на те, що використання першої достатньої ознаки екстремуму не вимагає диференціювання функції з точкою x 0 цим і спрощує обчислення.

Приклад 2

Знайти точки максимуму та мінімуму функції y = 1 6 x 3 = 2 x 2 + 22 3 x - 8.

Рішення.

Область визначення функції – це дійсні числа. Це можна записати у вигляді системи рівнянь виду:

1 6 x 3 - 2 x 2 - 22 3 x - 8 x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Після чого необхідно знайти похідну:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

Точка х = 0 немає похідної, оскільки значення односторонніх меж різні. Отримаємо, що:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 · (0 - 0) 2 - 4 · (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 · (0 + 0) 2 - 4 · (0 + 0) + 22 3 = + 22 3

Звідси випливає, що функція безперервна в точці х = 0 тоді обчислюємо

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 · (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 · (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 · 0 2 + 22 3 · 0 - 8 = - 8

Необхідно зробити обчислення для знаходження значення аргументу, коли похідна стає рівною нулю:

1 2 x 2 - 4 x - 22 3 x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 · 1 2 = 4 - 2 3 3 > 0

Усі отримані точки слід зазначити на прямий визначення знака кожного інтервалу. Тому необхідно обчислити похідну у довільних точках кожного інтервалу. Наприклад, у нас можна взяти точки зі значеннями x = -6, x = -4, x = -1, x = 1, x = 4, x = 6. Отримаємо, що

y "(-6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(-1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 · 4 2 - 4 · 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Зображення на прямий має вигляд

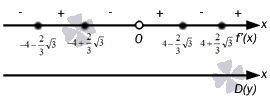
Отже, приходимо до того, що необхідно вдатися до першої ознаки екстремуму. Обчислимо та отримаємо, що

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , тоді звідси точки максимуму мають значення x = - 4 + 2 3 3 , x = 4 - 2 3 3

Перейдемо до обчислення мінімумів:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Зробимо обчислення максимумів функції. Отримаємо, що

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Графічне зображення

Відповідь:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 3 y m a = y 4 - 2 3 3 = 8 27 3

Якщо задана функція f "(x 0) = 0, тоді при її f "" (x 0) > 0 отримуємо, що x 0 є точкою мінімуму, якщо f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Приклад 3

Знайти максимуми та мінімуми функції y = 8 x x + 1 .

Рішення

Для початку знаходимо область визначення. Отримуємо, що

D(y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Необхідно продиференціювати функцію, після чого отримаємо

y " = 8 x x + 1 " = 8 · x " · (x + 1) - x · (x + 1) "(x + 1) 2 = = 8 · 1 2 x · (x + 1) - x · 1 (x + 1) 2 = 4 · x + 1 - 2 x (x + 1) 2 · x = 4 · - x + 1 (x + 1) 2 · x

При х = 1 похідна стає рівною нулю, отже, точка є можливим екстремумом. Для уточнення необхідно знайти другу похідну та обчислити значення за х = 1 . Отримуємо:

y "" = 4 · - x + 1 (x + 1) 2 · x " = = 4 · (- x + 1) " · (x + 1) 2 · x - (- x + 1) · x + 1 2 · x "(x + 1) 4 · x = = 4 · (- 1) · (x + 1) 2 · x - (- x + 1) · x + 1 2 " · x + (x + 1) 2 · x "(x + 1) 4 · x = = 4 · - (x + 1) 2 x - (- x + 1) · 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 · x = = - (x + 1) 2 x - (- x + 1) · x + 1 · 2 x + x + 1 2 x (x + 1) 4 · x = = 2 · 3 x 2 - 6 x - 1 x + 1 3 · x 3 ⇒ y "" (1) = 2 · 3 · 1 2 - 6 · 1 - 1 (1 + 1) 3 · (1) 3 = 2 · - 4 8 = - 1< 0

Значить, використавши 2 достатня умоваекстремуму, отримуємо, що х = 1 є точкою максимуму. Інакше запис має вигляд ym a x = y(1) = 8 1 1 + 1 = 4 .

Графічне зображення

Відповідь: y m a x = y(1) = 4..

Функція y = f(x) має її похідну до n-го порядку в околиці заданої точки x 0 і похідну до n + 1-го порядку в точці x 0 . Тоді f "(x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x0) = 0 .

Звідси випливає, що коли n є парним числом, то x 0 вважається точкою перегину, коли n є непарним числом, то x 0 точка екстремуму, причому f(n + 1) (x 0) > 0 тоді x 0 є точкою мінімуму, f(n+1) (x 0)< 0 , тогда x 0 является точкой максимума.

Приклад 4

Знайти точки максимуму та мінімуму функції y y = 1 16 (x + 1) 3 (x – 3) 4 .

Рішення

Вихідна функція – ціла раціональна, звідси випливає, що область визначення – всі дійсні числа. Потрібно продиференціювати функцію. Отримаємо, що

y" = 1 16 x + 1 3 "(x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Ця похідна звернеться в нуль при x 1 = - 1 x 2 = 5 7 x 3 = 3 . Тобто, точки можуть бути точками можливого екстремуму. Необхідно застосувати третю достатню умову екстремуму. Знаходження другої похідної дозволяє точно визначити наявність максимуму і мінімуму функції. Обчислення другої похідної проводиться у точках її можливого екстремуму. Отримуємо, що

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (-1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

Значить, що x 2 = 57 є точкою максимуму. Застосувавши 3 достатню ознаку, отримуємо, що за n = 1 і f (n + 1) 5 7< 0 .

Необхідно визначити характер точок x 1 = - 1 x 3 = 3 . Для цього необхідно знайти третю похідну, обчислити значення цих точках. Отримуємо, що

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Отже, x 1 = - 1 є точкою перегину функції, оскільки за n = 2 і f (n + 1) (- 1) ≠ 0 . Необхідно дослідити точку x3=3. Для цього знаходимо 4 похідну та робимо обчислення в цій точці:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96> 0

З вище вирішеного робимо висновок, що x3 = 3 є точкою мінімуму функції.

Графічне зображення

Відповідь: x 2 = 5 7 є точкою максимуму, x 3 = 3 – точкою мінімуму заданої функції.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Випускна робота у формі ЄДІ для 11-класників обов'язково містить завдання на обчислення меж, проміжків зменшення та зростання похідної функції, пошук точок екстремуму та побудова графіків. Хороші знанняцієї теми дозволяє правильно відповісти на кілька питань іспиту і не відчувати труднощів у подальшому професійному навчанні.

Основи диференціального обчислення – одна з головних тем математики сучасної школи. Вона вивчає застосування похідної для дослідження залежностей змінних – саме через похідну можна проаналізувати зростання та зменшення функції без звернення до креслення.

Комплексна підготовка випускників до здачі ЄДІна освітньому порталі«Школково» допоможе глибоко зрозуміти принципи диференціювання – докладно розібратися в теорії, вивчити приклади вирішення типових завдань та спробувати свої сили у самостійній роботі. Ми допоможемо вам ліквідувати прогалини у знаннях – уточнити уявлення про лексичні поняття теми та залежності величин. Учні зможуть повторити, як знаходити проміжки монотонності, що означає підйом або зменшення похідної функції на певному відрізку, коли граничні точки включаються і не включаються в знайдені інтервали.

Перш ніж розпочинати безпосереднє вирішення тематичних завдань, ми рекомендуємо спочатку перейти до розділу «Теоретична довідка» та повторити визначення понять, правила та табличні формули. Тут же можна прочитати, як знаходити та записувати кожен проміжок зростання та зменшення функції на графіку похідної.

Всі запропоновані відомості викладаються в максимально доступній формі для розуміння практично з нуля. На сайті доступні матеріали для сприйняття та засвоєння в кількох різних формах– читання, відеоперегляду та безпосереднього тренінгу під керівництвом досвідчених вчителів. Професійні педагогидокладно розкажуть, як знайти проміжки зростання та зменшення похідної функції аналітичними та графічними способами. У ході вебінарів можна буде поставити будь-яке питання, що цікавить як по теорії, так і з вирішення конкретних завдань.

Згадавши основні моменти теми, перегляньте приклади зростання похідної функції, аналогічні завданням екзаменаційних варіантів. Для закріплення засвоєного загляньте в «Каталог» - тут ви знайдете практичні вправи для самостійної роботи. Завдання у розділі підібрані різного рівняскладнощі з урахуванням напрацювання навичок. До кожного з них, наприклад, додаються алгоритми рішень і правильні відповіді.

Вибираючи розділ «Конструктор», учні зможуть попрактикуватися у дослідженні зростання та зменшення похідної функції реальних варіантах ЄДІ, які постійно оновлюються з урахуванням останніх змінта нововведень.

Похідний. Якщо похідна функції позитивна будь-якої точки інтервалу, то функція зростає, якщо негативна – зменшується.

Щоб знайти проміжки зростання та зменшення функції, потрібно знайти область її визначення, похідну, вирішити нерівності виду F'(x) > 0 і F'(x)

Рішення.

3. Вирішимо нерівності y' > 0 та y' 0;
(4 - x)/x³

Рішення.
1. Знайдемо область визначення функції. Очевидно, що вираз, що стоїть у знаменнику, повинен завжди бути відмінним від нуля. Тому 0 виключається з області визначення: функція визначена за x ∈ (-∞; 0)∪(0; +∞).

2. Обчислимо похідну функції:
y'(x) = ((3·x² + 2·x - 4)' ·x² – (3·x² + 2·x - 4) · (x²)')/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x - 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^ 4 = (8 · x - 2 · x²) / x^4 = 2 · (4 - x) / x³.

3. Вирішимо нерівності y' > 0 та y' 0;
(4 - x)/x³

4. Ліва частина нерівності має один дійсний х = 4 і звертається при x = 0. Тому значення x = 4 включається і в проміжок , і в проміжок спадання, а точка 0 не включається .
Отже, потрібна функція зростає на проміжку x ∈ (-∞; 0) ∪ .

4. Ліва частина нерівності має один дійсний х = 4 і звертається при x = 0. Тому значення x = 4 включається і в проміжок , і в проміжок спадання, а точка 0 не включається .
Отже, потрібна функція зростає на проміжку x ∈ (-∞; 0) ∪ .

Джерела:

• як знайти на функції проміжки зменшення

Функція є суворою залежністю одного числа від іншого, або значення функції (y) від аргументу (х). Кожен процес (не тільки в математиці) може бути описаний своєю функцією, яка буде мати характерні особливості: проміжки зменшення та зростання, точки мінімумів і максимумів і так далі.

Вам знадобиться

• - папір;
• - Ручка.

Інструкція

приклад 2.
Знайти проміжки спадання f(x)=sinx +x.
Похідна цієї функції дорівнюватиме: f'(x)=cosx+1.
Вирішуючи нерівність cosx+1

Інтервалом монотонностіфункції можна назвати проміжок, у якому функція або лише зростає, або лише зменшується. Ряд певних дій допоможе знайти такі діапазони для функції, що нерідко потрібно в алгебраїчних подібних завданнях.

Інструкція

Першим кроком у вирішенні задачі визначення інтервалів, в яких функція монотонно зростає або зменшується, стане обчислення даної функції. Для цього дізнайтеся всі значення аргументів (значення осі абсцис), для яких можна знайти значення функції. Позначте точки, де спостерігаються розриви. Знайдіть похідну функцію. Визначивши вираз, який є похідною, прирівняйте його до нуля. Після цього слід знайти коріння . Не про область допустимих.

Точки, в яких функція або в яких її похідна дорівнює нулю, є межі інтервалів монотонності. Ці діапазони, а також точки, що їх поділяють, слід послідовно внести до таблиці. Знайдіть похідну функцію в отриманих проміжках. Для цього підставте у вираз, що відповідає похідній, будь-який аргумент з інтервалу. Якщо результат позитивний, функція в даному діапазоні зростає, інакше - зменшується. Результати вносяться до таблиці.

У рядок, що позначає похідну функції f'(x), записується відповідний значенням аргументів: "+" - якщо похідна позитивна, "-" - негативна або "0" - дорівнює нулю. У наступному рядку позначте монотонність самого вихідного виразу. Стрілка вгору відповідає зростанню, вниз – спадання. Позначте функції. Це точки, у яких похідна дорівнює нулю. Екстремум може бути точкою максимуму, або точкою мінімуму. Якщо попередня ділянка функції зростала, а поточна зменшується, це точка максимуму. У разі, коли до цієї точки функція зменшувалась, а тепер зростає – це точка мінімуму. Внесіть у таблицю значення функції у точках екстремуму.

Джерела:

• що таке визначення монотонність

Дослідження поведінки функції, що має складну залежність від аргументу, проводиться за допомогою похідної. За характером зміни похідної можна знайти критичні точки та ділянки зростання чи зменшення функції.

"Зростання та зменшення функції"

Цілі уроку:

1. Навчити знаходити проміжки монотонності.

2. Розвиток розумових здібностей, які забезпечують аналіз ситуації та розробку адекватних способів дії (аналіз, синтез, порівняння).

3. Формування інтересу до предмета.

Сьогодні ми продовжуємо вивчати додаток похідної і розглянемо питання про її застосування дослідженню функцій. Фронтальна робота

А тепер дамо деякі визначення властивостей функції “Мозковий штурм”

1. Що називають функцією?

2. Як називається змінна Х?

3. Як називається змінна Y?

4. Що називається областю визначення функції?

5. Що називається безліччю значення функції?

6. Яка функція називається парною?

7. Яка функція називається непарною?

8. Що можна сказати про графік парної функції?

9. Що можна сказати про графік непарної функції?

10. Яка функція називається зростаючою?

11. Яка функція називається спадною?

12. Яка функція називається періодичною?

Математика вивчає математичні моделі. Однією з найголовніших математичних моделейє функція. Існують різні способиопис функцій. Який найнаочніший?

- Графічний.

– Як побудувати графік?

- По точках.

Цей спосіб підійде, якщо заздалегідь відомо, як виглядає графік. Наприклад, що є графіком квадратичні функції, лінійної функції, зворотної пропорційності, Функції y = sinx? (Демонструються відповідні формули, учні називають криві, що є графіками.)

А що якщо потрібно побудувати графік функції чи ще складнішої? Чи можна знайти кілька точок, але як поводиться функція між цими точками?

Поставити на дошці дві точки, попросити учнів показати, як може виглядати графік між ними:

З'ясувати, як поводиться функція, допомагає її похідна.

Відкрийте зошити, запишіть номер, класна робота.

Мета уроку: дізнатися, як пов'язаний графік функції з графіком її похідної, та навчитися вирішувати завдання двох видів:

1. За графіком похідної знаходити проміжки зростання та зменшення самої функції, а також точки екстремуму функції;

2. За схемою знаків похідної на проміжках знаходити інтервали зростання та зменшення самої функції, а також точки екстремуму функції.

Подібні завдання відсутні у наших підручниках, але зустрічаються у тестах єдиного державного іспиту(Частина А і В).

Сьогодні на уроці ми розглянемо невеликий елемент роботи другого етапу вивчення процесу, дослідження однієї з властивостей функції – визначення проміжків монотонності

Для вирішення поставленого завдання нам необхідно згадати деякі питання, розглянуті раніше.

Отже, запишемо тему сьогоднішнього уроку: Ознаки зростання та зменшення функції.

Ознаки зростання та зменшення функції:

Якщо похідна цієї функції позитивна всім значень x в інтервалі (а; в), тобто.f"(x) > 0, то функція в цьому інтервалі зростає.
Якщо похідна цієї функції негативна всім значень x в інтервалі(а; в), тобто.f"(x)< 0, то функция в этом интервале убывает

Порядок знаходження проміжків монотонності:

Знайти область визначення функції.

1. Знайти першу похідну функції.

2. вирішувати самій на дошці

Знайти критичні точки, дослідити знак першої похідної у проміжках, куди знайдені критичні точки ділять область визначення функції. Знайти проміжки монотонності функцій:

а) область визначення,

б) знайдемо першу похідну:,

в) знайдемо критичні точки: ; , і

3. Досліджуємо знак похідної отриманих проміжках, рішення представимо як таблиці.

вказати на точки екстремуму

Розглянемо кілька прикладів дослідження функції зростання і спадання.

Достатня умова існування максимуму полягає у зміні похідної знака при переході через критичну точку з "+" на "-", а для мінімуму з "-" на "+". Якщо при переході через критичну точку зміни похідного знака не відбувається, то в даній точці екстремуму немає

1. Знайти Д(f).

2. Знайти f "(x).

3. Знайти стаціонарні точки, тобто. точки, де f"(x) = 0 або f"(x) не існує.
(Виробна дорівнює 0 в нулях чисельника, похідна не існує в нулях знаменника)

4. Розташувати Д(f) та ці точки на координатній прямій.

5. Визначити знаки похідної кожному з інтервалів

6. Застосувати ознаки.

7. Записати відповідь.

Закріплення нового матеріалу.

Учні працюють у парах, рішення записують у зошитах.

а) у = х? - 6 х? + 9 х - 9;

б) у = 3х2 - 5х + 4.

Двоє працюють біля дошки.

а) у = 2 х ³ – 3 х ² – 36 х + 40

б) у = х4-2 х³

3.Підсумок уроку

Домашнє завдання: тест (диференційований)