Зростання, спадання та екстремуми функції. Достатні ознаки зростання та зменшення функції

"Зростання та зменшення функції"

Цілі уроку:

1. Навчити знаходити проміжки монотонності.

2. Розвиток розумових здібностей, які забезпечують аналіз ситуації та розробку адекватних способів дії (аналіз, синтез, порівняння).

3. Формування інтересу до предмета.

Хід уроку

Сьогодні ми продовжуємо вивчати додаток похідної і розглянемо питання про її застосування до дослідження функцій. Фронтальна робота

А тепер дамо деякі визначення властивостей функції “Мозковий штурм”

1. Що називають функцією?

2. Як називається змінна Х?

3. Як називається змінна Y?

4. Що називається областю визначення функції?

5. Що називається безліччю значення функції?

6. Яка функція називається парною?

7. Яка функція називається непарною?

8. Що можна сказати про графік парної функції?

9. Що можна сказати про графік непарної функції?

10. Яка функція називається зростаючою?

11. Яка функція називається спадною?

12. Яка функція називається періодичною?

Математика вивчає математичні моделі. Однією з найголовніших математичних моделейє функція. Існують різні способиопис функцій. Який найнаочніший?

- Графічний.

– Як побудувати графік?

- По точках.

Цей спосіб підійде, якщо заздалегідь відомо, як виглядає графік. Наприклад, що є графіком квадратичні функції, лінійної функції, зворотної пропорційності, Функції y = sinx? (Демонструються відповідні формули, учні називають криві, що є графіками.)

А що якщо потрібно побудувати графік функції чи ще складнішої? Можна знайти кілька точок, але як поводиться функція між цими точками?

Поставити на дошці дві точки, попросити учнів показати, як може виглядати графік між ними:

З'ясувати, як поводиться функція, допомагає її похідна.

Відкрийте зошити, запишіть номер, класна робота.

Мета уроку: дізнатися, як пов'язаний графік функції з графіком її похідної, та навчитися вирішувати завдання двох видів:

1. За графіком похідної знаходити проміжки зростання та зменшення самої функції, а також точки екстремуму функції;

2. За схемою знаків похідної на проміжках знаходити інтервали зростання та зменшення самої функції, а також точки екстремуму функції.

Подібні завдання відсутні у наших підручниках, але зустрічаються у тестах єдиного державного іспиту(Частина А і В).

Сьогодні на уроці ми розглянемо невеликий елемент роботи другого етапу вивчення процесу, дослідження однієї з властивостей функції – визначення проміжків монотонності

Для вирішення поставленого завдання нам необхідно згадати деякі питання, розглянуті раніше.

Отже, запишемо тему сьогоднішнього уроку: Ознаки зростання та зменшення функції.

Ознаки зростання та зменшення функції:

Якщо похідна цієї функції позитивна всім значень x в інтервалі (а; в), тобто.f"(x) > 0, то функція в цьому інтервалі зростає.
Якщо похідна цієї функції негативна всім значень x в інтервалі(а; в), тобто.f"(x)< 0, то функция в этом интервале убывает

Порядок знаходження проміжків монотонності:

Знайти область визначення функції.

1. Знайти першу похідну функції.

2. вирішувати самій на дошці

Знайти критичні точки, дослідити знак першої похідної у проміжках, куди знайдені критичні точки ділять область визначення функції. Знайти проміжки монотонності функцій:

а) область визначення,

б) знайдемо першу похідну:,

в) знайдемо критичні точки: ; , і

3. Досліджуємо знак похідної отриманих проміжках, рішення представимо як таблиці.

вказати на точки екстремуму

Розглянемо кілька прикладів дослідження функції зростання і спадання.

Достатня умоваІснування максимуму полягає у зміні знака похідної при переході через критичну точку з "+" на "-", а для мінімуму з "-" на "+". Якщо при переході через критичну точку зміни похідного знака не відбувається, то в даній точці екстремуму немає

1. Знайти Д(f).

2. Знайти f "(x).

3. Знайти стаціонарні точки, тобто. точки, де f"(x) = 0 або f"(x) не існує.
(Виробна дорівнює 0 в нулях чисельника, похідна не існує в нулях знаменника)

4. Розташувати Д(f) та ці точки на координатній прямій.

5. Визначити знаки похідної кожному з інтервалів

6. Застосувати ознаки.

7. Записати відповідь.

Закріплення нового матеріалу.

Учні працюють у парах, рішення записують у зошитах.

а) у = х? - 6 х? + 9 х - 9;

б) у = 3х2 - 5х + 4.

Двоє працюють біля дошки.

а) у = 2 х ³ – 3 х ² – 36 х + 40

б) у = х4-2 х³

3.Підсумок уроку

Домашнє завдання: тест (диференційований)

Визначення зростаючої функції.

Функція y=f(x)зростає на інтервалі X, якщо для будь-яких і виконується нерівність. Інакше кажучи – більшого значення аргументу відповідає більше значення функції.

Визначення спадної функції.

Функція y=f(x)зменшується на інтервалі X, якщо для будь-яких і виконується нерівність . Інакше кажучи – більшого значення аргументу відповідає менше значення функції.

ПРИМІТКА: якщо функція визначена і безперервна в кінцях інтервалу зростання або спадання (a; b), тобто при x=aі x=b, то ці точки включаються в проміжок зростання або спадання. Це не суперечить визначенням зростаючої та спадної функції на проміжку X.

Наприклад, з властивостей основних елементарних функцій ми знаємо, що y=sinxвизначена та безперервна для всіх дійсних значень аргументу. Тому з зростання функції синуса на інтервалі ми можемо стверджувати про зростання на відрізку .

Крапки екстремуму, екстремуми функції.

Точку називають точкою максимумуфункції y=f(x)якщо для всіх xз її околиці справедлива нерівність. Значення функції у точці максимуму називають максимумом функціїі позначають.

Точку називають точкою мінімумуфункції y=f(x)якщо для всіх xз її околиці справедлива нерівність. Значення функції у точці мінімуму називають мінімумом функціїі позначають.

Під околицею точки розуміють інтервал , де - Досить мале позитивне число.

Точки мінімуму та максимуму називають точками екстремуму, а значення функції, що відповідають точкам екстремуму, називають екстремумами функції.

Не плутайте екстремуми функції з найбільшим та найменшим значеннямфункції.

На першому малюнку найбільше значення функції на відрізку досягається в точці максимуму і дорівнює максимуму функції, а на другому малюнку - найбільше значення функції досягається в точці x=bяка не є точкою максимуму.

Достатні умови зростання та зменшення функції.

На підставі достатніх умов (ознак) зростання та зменшення функції знаходяться проміжки зростання та зменшення функції.

Ось формулювання ознак зростання та зменшення функції на інтервалі:

якщо похідна функції y=f(x)позитивна для будь-кого xз інтервалу X, то функція зростає на X;

якщо похідна функції y=f(x)негативна для будь-кого xз інтервалу X, то функція зменшується на X.

Таким чином, щоб визначити проміжки зростання та зменшення функції необхідно:

Розглянемо приклад знаходження проміжків зростання та зменшення функції для роз'яснення алгоритму.

приклад.

Знайти проміжки зростання та зменшення функції .

Рішення.

Першим кроком є знаходження обросту визначення функції. У прикладі вираз у знаменнику має звертатися в нуль, отже, .

Переходимо до знаходження похідної функції:

Для визначення проміжків зростання та зменшення функції за достатньою ознакою вирішуємо нерівності і на області визначення. Скористайтеся узагальненням методу інтервалів. Єдиним дійсним коренем чисельника є x = 2, а знаменник звертається в нуль при x=0. Ці точки розбивають область визначення інтервали, у яких похідна функції зберігає знак. Зазначимо ці точки на числовій прямій. Плюсами та мінусами умовно позначимо інтервали, на яких похідна позитивна чи негативна. Стрілки знизу схематично показують зростання або зменшення функції на відповідному інтервалі.

Нехай на площині задана прямокутна система координат. Графіком деякої функції , (X-область визначення) називається безліч точок цієї площини з координатами, де .

Для побудови графіка потрібно зобразити на площині множину точок, координати яких (x; y) пов'язані співвідношенням .

Найчастіше графіком функції є певна крива.

Найпростіший спосіб побудови графіка – побудова за точками.

Складається таблиця, у якій одному осередку стоїть значення аргументу, а протилежної їй значення функції від цього аргументу. Потім отримані точки відзначаються на площині і через них проводиться крива.

Приклад побудови за точками графіка функції:

Побудуємо таблицю.

Тепер будуємо графік.

Але в такий спосіб не завжди можливо побудувати досить точний графік – для точності потрібно брати дуже багато точок. Тому використовують різні методидослідження функції.

З повною схемою дослідження функції знайомляться у вищих навчальних закладах. Одним із пунктів дослідження функції є знаходження проміжків зростання (зменшення) функції.

Функція називається зростаючою (убутною) на деякому проміжку, якщо для будь-яких x 2 і x 1 з цього проміжку, таких, що x 2 >x 1 .

Наприклад, функція, графік якої зображено на наступному малюнку, на проміжках зростає, але в проміжку (-5;3) зменшується. Тобто на проміжках графік йде "в гору". На проміжку (-5;3) «під гору».

Ще одним із пунктів дослідження функції є дослідження функції на періодичність.

Функція називається періодичною, якщо існує таке число T, що .

Число T називають періодом функції. Наприклад, функція періодична, тут період дорівнює 2П, так

Приклади графіків періодичних функцій:

Період першої функції дорівнює 3, а другий - 4.

Функція називається парною, якщо приклад парної функції y=x 2 .

Функція називається непарною, якщо Приклад непарної функції y=x3.

Графік парної функції симетричний щодо осі ОУ (осьова симетрія).

Графік непарної функції симетричний щодо початку координат (центральна симетрія).

Приклади графіків парної (ліворуч) та непарної (праворуч) функції.

Похідний. Якщо похідна функції позитивна будь-якої точки інтервалу, то функція зростає, якщо негативна – зменшується.

Щоб знайти проміжки зростання та зменшення функції, потрібно знайти область її визначення, похідну, вирішити нерівності виду F'(x) > 0 і F'(x)

Рішення.

3. Вирішимо нерівності y' > 0 та y' 0;
(4 - x)/x³

Рішення.
1. Знайдемо область визначення функції. Очевидно, що вираз, що стоїть у знаменнику, повинен завжди бути відмінним від нуля. Тому 0 виключається з області визначення: функція визначена за x ∈ (-∞; 0)∪(0; +∞).

2. Обчислимо похідну функції:
y'(x) = ((3·x² + 2·x - 4)' ·x² – (3·x² + 2·x - 4) · (x²)')/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x - 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^ 4 = (8 · x - 2 · x²) / x^4 = 2 · (4 - x) / x³.

3. Вирішимо нерівності y' > 0 та y' 0;
(4 - x)/x³

4. Ліва частина нерівності має один дійсний х = 4 і звертається при x = 0. Тому значення x = 4 включається і в проміжок , і в проміжок спадання, а точка 0 не включається .
Отже, потрібна функція зростає на проміжку x ∈ (-∞; 0) ∪ .

Джерела:

як знайти на функції проміжки зменшення

Функція є суворою залежністю одного числа від іншого, або значення функції (y) від аргументу (х). Кожен процес (не тільки в математиці) може бути описаний своєю функцією, яка буде мати характерні особливості: проміжки зменшення та зростання, точки мінімумів і максимумів і так далі.

Вам знадобиться

- папір;
- Ручка.

Інструкція

приклад 2.
Знайти проміжки спадання f(x)=sinx +x.
Похідна цієї функції дорівнюватиме: f'(x)=cosx+1.
Вирішуючи нерівність cosx+1

Інтервалом монотонностіфункції можна назвати проміжок, у якому функція або лише зростає, або лише зменшується. Ряд певних дій допоможе знайти такі діапазони для функції, що нерідко потрібно в алгебраїчних подібних завданнях.

Інструкція

Першим кроком у вирішенні задачі визначення інтервалів, в яких функція монотонно зростає або зменшується, стане обчислення даної функції. Для цього дізнайтеся всі значення аргументів (значення осі абсцис), для яких можна знайти значення функції. Позначте точки, де спостерігаються розриви. Знайдіть похідну функцію. Визначивши вираз, який є похідною, прирівняйте його до нуля. Після цього слід знайти коріння . Не про область допустимих.

Точки, в яких функція або в яких її похідна дорівнює нулю, є межі інтервалів монотонності. Ці діапазони, а також точки, що їх поділяють, слід послідовно внести до таблиці. Знайдіть похідну функцію в отриманих проміжках. Для цього підставте у вираз, що відповідає похідній, будь-який аргумент з інтервалу. Якщо результат позитивний, функція в даному діапазоні зростає, інакше - зменшується. Результати вносяться до таблиці.

У рядок, що позначає похідну функції f'(x), записується відповідний значенням аргументів: "+" - якщо похідна позитивна, "-" - негативна або "0" - дорівнює нулю. У наступному рядку позначте монотонність самого вихідного виразу. Стрілка вгору відповідає зростанню, вниз – спадання. Позначте функції. Це точки, у яких похідна дорівнює нулю. Екстремум може бути точкою максимуму, або точкою мінімуму. Якщо попередня ділянка функції зростала, а поточна зменшується, це точка максимуму. У разі, коли до цієї точки функція зменшувалась, а тепер зростає – це точка мінімуму. Внесіть у таблицю значення функції у точках екстремуму.

Джерела:

що таке визначення монотонність

Дослідження поведінки функції, що має складну залежність від аргументу, проводиться за допомогою похідної. За характером зміни похідної можна знайти критичні точки та ділянки зростання чи зменшення функції.

Екстремуми функції

Визначення 2

Точка $x_0$ називається точкою максимуму функції $f(x)$, якщо є така околиця даної точки, що всім $x$ з цієї околиця виконується нерівність $f(x)\le f(x_0)$.

Визначення 3

Точка $x_0$ називається точкою максимуму функції $f(x)$, якщо є така околиця даної точки, що всім $x$ з цієї околиця виконується нерівність $f(x)\ge f(x_0)$.

Поняття екстремуму функції тісно пов'язані з поняттям критичної точки функції. Введемо її визначення.

Визначення 4

$x_0$ називається критичною точкоюфункції $f(x)$, якщо:

1) $x_0$ - внутрішня точка області визначення;

2) $f"\left(x_0\right)=0$ або немає.

Для поняття екстремуму можна сформулювати теореми про достатні та необхідні умови його існування.

Теорема 2

Достатня умова екстремуму

Нехай точка $ x_0 $ є критичною для функції $ y = f (x) $ і лежить в інтервалі $ (a, b) $. Нехай кожному інтервалі $\left(a,x_0\right)\ і\ (x_0,b)$ похідна $f"(x)$ існує і зберігає постійний знак.

1) Якщо на інтервалі $(a,x_0)$ похідна $f"\left(x\right)>0$, а на інтервалі $(x_0,b)$ похідна $f"\left(x\right)

2) Якщо інтервалі $(a,x_0)$ похідна $f"\left(x\right)0$, то точка $x_0$ - точка мінімуму цієї функції.

3) Якщо і на інтервалі $(a,x_0)$, і на інтервалі $(x_0,b)$ похідна $f"\left(x\right) >0$ або похідна $f"\left(x\right)

Ця теорема проілюстрована малюнку 1.

Рисунок 1. Достатня умова існування екстремумів

Приклади екстремумів (рис. 2).

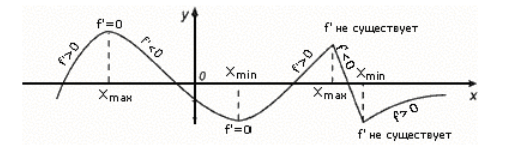
Рисунок 2. Приклади точок екстремумів

Правило дослідження функції на екстремум

2) Знайти похідну $f"(x)$;

7) Зробити висновки про наявність максимумів і мінімумів кожному проміжку, використовуючи теорему 2.

Зростання та зменшення функції

Введемо, для початку, визначення зростаючої та спадної функцій.

Визначення 5

Функція $y=f(x)$, визначена на проміжку $X$, називається зростаючою, якщо для будь-яких точок $x_1,x_2\in X$ при $x_1

Визначення 6

Функція $y=f(x)$, визначена на проміжку $X$, називається спадною, якщо будь-яких точок $x_1,x_2\in X$ при $x_1f(x_2)$.

Дослідження функції на зростання та спадання

Дослідити функції на зростання та зменшення можна за допомогою похідної.

Для того щоб дослідити функцію на проміжки зростання та спадання, необхідно зробити наступне:

1) Знайти область визначення функції $ f (x) $;

2) Знайти похідну $f"(x)$;

3) Знайти точки, у яких виконується рівність $f"\left(x\right)=0$;

4) Знайти точки, де $f"(x)$ немає;

5) Відзначити на координатній прямій усі знайдені точки та область визначення цієї функції;

6) Визначити знак похідної $f"(x)$ на кожному проміжку, що вийшов;

7) Зробити висновок: на проміжках, де $f"\left(x\right)0$ функція зростає.

Приклади завдань на дослідження функцій на зростання, спад та наявність точок екстремумів

Приклад 1

Дослідити функцію на зростання і зменшення, і наявність точок максимумів і мінімумів: $f(x)=(2x)^3-15x^2+36x+1$

Так як перші 6 пунктів збігаються, проведемо для початку їх.

1) Область визначення – всі дійсні числа;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $ f "\ left (x \ right) = 0 $;

\ \ \

4) $f"(x)$ існує у всіх точках області визначення;

5) Координатна пряма:

Малюнок 3.

6) Визначити знак похідної $f"(x)$ на кожному проміжку:

\ \}