Теорема гауса для електричної індукції вектор. Потік вектор електричної індукції

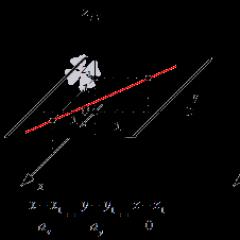
Введемо поняття потоку вектора електричної індукції. Розглянемо нескінченно малий майданчик. Найчастіше необхідно знати як величину майданчика, а й її орієнтацію у просторі. Введемо поняття вектор-майданчик. Умовимося під вектором-майданчиком розуміти вектор, спрямований перпендикулярно до майданчика і чисельно рівної величини майданчика.

Рисунок 1 – До визначення вектора – майданчики

Назвемо потоком вектора через майданчик
скалярний добуток векторів і
. Таким чином,

Потік вектора через довільну поверхню знаходиться інтегруванням всіх елементарних потоків

(4)

Якщо поле однорідне та плоска поверхня розташована перпендикулярно до поля, то:

. (5)

Наведений вираз визначає кількість силових ліній, що пронизують майданчик за одиницю часу.

Теорема Остроградського-Гаусса. Дивергенція напруженості електричного поля

Потік вектора електричної індукції через довільну замкнуту поверхню дорівнює сумі алгебри вільних електричних зарядів , що охоплюються цією поверхнею

(6)

Вираз (6) є теорему О-Г в інтегральному вигляді. Теорема 0-Г оперує з інтегральним (сумарним) ефектом, тобто. якщо
то невідомо, чи означає це відсутність зарядів у всіх точках досліджуваної частини простору, або, що сума позитивних і негативних зарядів, розташованих у різних точках цього простору дорівнюють нулю.

Для знаходження розташованих зарядів та їх величини по заданому полю необхідне співвідношення, що зв'язує вектор електричної індукції у цій точці із зарядом у тій же точці.

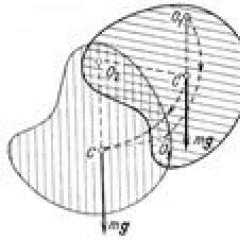
Припустимо, що нам потрібно визначити наявність заряду в точці а(Рис.2)

Рисунок 2 – До розрахунку дивергенції вектора

Застосуємо теорему О-Г. Потік вектора електричної індукції через довільну поверхню, що обмежує об'єм, в якому знаходиться точка. а, дорівнює

Алгебраїчну суму зарядів в обсязі можна записати як об'ємний інтеграл

(7)

де - заряд, віднесений до одиниці обсягу ;

- Елемент обсягу.

Для отримання зв'язку між полем та зарядом у точці абудемо зменшувати обсяг, стягуючи поверхню до точки а. При цьому розділимо обидві частини нашої рівності на величину . Переходячи до межі, отримаємо:

.

Права частина отриманого виразу є визначення об'ємної щільністю заряду в розглянутій точці простору. Ліва частина є межею відношення потоку вектора електричної індукції через замкнуту поверхню до об'єму, обмеженого цією поверхнею, коли обсяг прагне до нуля. Ця скалярна величина є важливою характеристикою електричного поля і має назву вектор дивергенції .

Таким чином:

,

отже

, (8)

де - Об'ємна щільність заряду.

З допомогою цього співвідношення легко вирішується зворотне завдання електростатики, тобто. знаходження розподілених зарядів за відомим полем.

Якщо вектор заданий, значить відомі його проекції
,
,
на координатні осі як функції координат і для обчислення розподіленої щільності зарядів, що створили задане поле, виявляється достатньо знайти суму трьох похідних похідних цих проекцій по відповідним змінним. У тих точках для яких
зарядів немає. У точках де
позитивна, є позитивний заряд з об'ємною щільністю, що дорівнює
, а в тих точках де
матиме негативне значення, знаходиться негативний заряд, щільність якого визначається значенням дивергенції.

Вираз (8) представляє теорему 0-Г у диференційній формі. У такій формі теорема показує, що джерелами електричного поля є вільні електричні заряди;силові лінії вектора електричної індукції починаються та закінчуються відповідно на позитивних та негативних зарядах.

Розглянемо, як змінюється значення вектора Е межі розділу двох середовищ, наприклад, повітря (ε 1) і води (ε = 81). Напруженість поля у воді зменшується стрибком у 81 раз. Така поведінка вектора Естворює певні незручності при розрахунку полів у різних середовищах. Щоб уникнути цієї незручності, вводять новий вектор. D- Вектор індукції або електричного зміщення поля. Зв'язок векторів Dі Емає вигляд

D = ε ε 0 Е.

Очевидно, для поля точкового заряду електричне зміщення буде рівне

Неважко побачити, що електричне зміщення вимірюється в Кл/м 2 не залежить від властивостей і графічно зображується лініями, аналогічними лініям напруженості.

Напрямок силових ліній поля характеризує напрямок поля в просторі (силові лінії, звичайно, не існують, їх вводять для зручності ілюстрації) або напрямок вектора напруженості поля. З допомогою ліній напруженості можна характеризувати як напрям, а й величину напруженості поля. Для цього умовилися проводити їх з певною густотою, так, щоб число ліній напруженості, що пронизують одиницю поверхні, перпендикулярної лініям напруженості, було пропорційно модулю вектора Е(Мал. 78). Тоді число ліній, що пронизують елементарний майданчик dS, нормаль до якого nутворює кут α із вектором Е, дорівнює E dScos = E n dS,

де E n - складова вектора Еу напрямку нормалі n. Величину dФ Е = E n dS = E d Sназивають потоком вектора напруженості через майданчик d S(d S= dS · n).

Для довільної замкнутої поверхні S потік вектора Ечерез цю поверхню дорівнює

Аналогічний вираз має потік вектора електричного усунення Ф D

.

Теорема Остроградського-Гаусса

Ця теорема дозволяє визначити потік векторів Е та D від будь-якої кількості зарядів. Візьмемо точковий заряд Q і визначимо потік вектора Ечерез кульову поверхню радіуса r в центрі якої він розташований.

Для кульової поверхні α = 0, cos α = 1, E n = E, S = 4 πr 2 і

Ф E = E · 4 πr 2 .

Підставляючи вираз для Е отримаємо

Таким чином, з кожного точкового заряду виходить потік ФЕ вектора Ерівний Q/ε0. Узагальнюючи цей висновок загальний випадок довільного числа точкових зарядів дають формулювання теореми: повний потік вектора Ечерез замкнуту поверхню довільної форми чисельно дорівнює сумі алгебри електричних зарядів, укладених усередині цієї поверхні, поділеної на ε 0 , тобто.

Для потоку вектора електричного зміщення Dможна отримати аналогічну формулу

потік вектора індукції через замкнуту поверхню дорівнює сумі алгебри електричних зарядів, охоплюваних цією поверхнею.

Якщо взяти замкнуту поверхню, що не охоплює заряду, то кожна лінія Еі Dбудуть перетинати цю поверхню двічі – на вході та виході, тому сумарний потік виявляється рівним нулю. Тут необхідно враховувати суму алгебри ліній, що входять і виходять.

Застосування теореми Остроградського-Гаусса для розрахунку електричних полів, створюваних площинами, сферою та циліндром

Сферична поверхня радіуса R несе на собі заряд Q, рівномірно розподілений поверхнею з поверхневою щільністю σ

Візьмемо точку А поза сферою на відстані r від центру і подумки проведемо сферу радіуса r симетричну зарядженою (рис. 79). Її площа S = 4 πr 2 . Потік вектора Е дорівнюватиме

За теоремою Остроградського-Гаусса
, отже,
враховуючи, що Q = σ·4 πr 2 отримаємо

Для точок, що знаходяться на поверхні сфери (R = r)

Д ля точок, що знаходяться всередині порожньої сфери (всередині сфери немає заряду), Е = 0.

2 . Порожниста циліндрична поверхня радіусом R і довжиною lзаряджена з постійною поверхневою щільністю заряду
(Мал. 80). Проведемо коаксіальну циліндричну поверхню радіусу > R.

Потік вектора Ечерез цю поверхню

За теоремою Гауса

Прирівнюючи праві частини наведених рівностей, отримаємо

.

Якщо задана лінійна щільність заряду циліндра (або тонкої нитки)
то

3. Поле нескінченних площин із поверхневою щільністю заряду σ (рис. 81).

Розглянемо поле, яке створюється нескінченною площиною. З міркувань симетрії випливає, що напруженість у будь-якій точці поля має напрямок, перпендикулярний до площини.

У симетричних точках Є однакова за величиною і протилежна за напрямом.

Побудуємо подумки поверхню циліндра з основою ΔS. Тоді через кожну з основ циліндра виходитиме потік

Ф Е = Е ΔS, а сумарний потік через циліндричну поверхню дорівнюватиме Ф Е = 2Е ΔS.

Усередині поверхні укладено заряд Q = σ · ΔS. Відповідно до теореми Гауса має виконуватися

звідки

Отриманий результат залежить від висоти обраного циліндра. Таким чином, напруженість поля Е на будь-яких відстанях однакова за величиною.

Для двох різноіменно заряджених площин з однаковою поверхневою щільністю заряду σ за принципом суперпозиції поза простором між площинами напруженість поля дорівнює нулю Е = 0, а у просторі між площинами
(Рис. 82а). Якщо площини заряджені однойменними зарядами з однаковою поверхневою щільністю зарядів, спостерігається зворотна картина (рис. 82б). У просторі між площинами Е=0, а просторі за межами площин
.

Потік вектор напруженості електричного поля.Нехай невеликий майданчик DS(рис.1.2) перетинають силові лінії електричного поля, напрямок яких складає з нормаллю n до цього майданчика кут a. Вважаючи, що вектор напруженості Е не змінюється у межах майданчика DS, визначимо потік вектора напруженостічерез майданчик DSяк

DFE =E DS cos a.(1.3)

Оскільки густота силових ліній дорівнює чисельному значенню напруженості E, то кількість силових ліній, що перетинають майданчикDS, буде чисельно дорівнює значенню потокуDFEчерез поверхнюDS. Представимо праву частину виразу (1.3) як скалярний добуток векторів EіDS= nDS, де n– одиничний вектор нормалі до поверхніDS. Для елементарного майданчика d Sвираз (1.3) набуває вигляду

dFE = E d S

Через весь майданчик Sпотік вектора напруженості обчислюється як інтеграл поверхнею

Потік вектор електричної індукції.Потік вектора електричної індукції визначається аналогічно до потоку вектора напруженості електричного поля

dFD = D d S

У визначеннях потоків помітна деяка неоднозначність, пов'язана з тим, що для кожної поверхні можна задати дві нормалі протилежного спрямування. Для замкнутої поверхні позитивною вважається зовнішня нормаль.

Теорема Гауса.Розглянемо точковий позитивнийелектричний заряд q, що знаходиться всередині довільної замкнутої поверхні S(Рис. 1.3). Потік вектор індукції через елемент поверхні d Sдорівнює
(1.4)

Складову d S D = d S cos aелемента поверхні d Sу напрямку вектора індукціїDрозглядаємо як елемент сферичної поверхні радіусу r, у центрі якої розташований зарядq.

Враховуючи, що d S D/ r 2 дорівнює елементарному тілесномукутку dw, під яким з точки знаходження зарядуqвидно елемент поверхні d S, Перетворимо вираз (1.4) на вигляд d FD = q d w / 4 pзвідки після інтегрування по всьому навколишньому заряду простору, тобто в межах тілесного кута від 0 до 4p, отримаємо

FD = q.

Потік вектора електричної індукції через замкнуту поверхню довільної форми дорівнює заряду, укладеному всередині цієї поверхні.

Якщо довільна замкнута поверхня Sне охоплює точковий заряд q(Рис. 1.4), то, побудувавши конічну поверхню з вершиною в точці знаходження заряду, розділимо поверхню Sна дві частини: S 1 і S 2 . Потік вектора D через поверхню Sзнайдемо як суму алгебри потоків через поверхні S 1 і S 2:

.

Обидві поверхні з точки знаходження заряду qвидно під одним тілесним кутом w. Тому потоки рівні

Оскільки для обчислення потоку через замкнуту поверхню використовується зовнішня нормальдо поверхні, легко бачити, що потік Ф 1D < 0, тогда как поток Ф2D> 0. Сумарний потік Ф D= 0. Це означає, що потік вектора електричної індукції через замкнуту поверхню довільної форми не залежить від зарядів, розташованих поза цією поверхнею.

Якщо електричне поле створюється системою точкових зарядів q 1 , q 2 ,¼ , q n, яка охоплюється замкнутою поверхнею S, то відповідно до принципу суперпозиції, потік вектора індукції через цю поверхню визначається як сума потоків, створюваних кожним із зарядів. Потік вектора електричної індукції через замкнуту поверхню довільної форми дорівнює сумі алгебри зарядів, охоплених цією поверхнею:

Слід зазначити, що заряди q iне обов'язково повинні бути точковими, необхідна умова – заряджена область має повністю охоплюватися поверхнею. Якщо у просторі, обмеженому замкненою поверхнею S, Електричний заряд розподілений безперервно, слід вважати, що кожен елементарний об'єм d Vмає заряд. У цьому випадку в правій частині виразу (1.5) алгебраїчне підсумовування зарядів замінюється інтегруванням за обсягом, укладеним усередині замкнутої поверхні S:

(1.6)

Вираз (1.6) є найбільш загальним формулюванням теореми Гауса: потік вектора електричної індукції через замкнуту поверхню довільної форми дорівнює сумарному заряду в обсязі, охопленому цією поверхнею, і не залежить від зарядів, розташованих поза розглянутою поверхнею. Теорему Гауса можна записати і для потоку вектора напруженості електричного поля:

.

З теореми Гаусса випливає важлива властивість електричного поля: силові лінії починаються або закінчуються тільки на електричних зарядах або йдуть у нескінченність. Ще раз підкреслимо, що незважаючи на те, що напруженість електричного поля E та електрична індукція D залежать від розташування у просторі всіх зарядів, потоки цих векторів через довільну замкнуту поверхню Sвизначаються лише тими зарядами, які розташовані всередині поверхні S.

Диференційна форма теореми Гауса.Відмітимо, що інтегральна форматеореми Гаусса характеризує співвідношення між джерелами електричного поля (зарядами) та характеристиками електричного поля (напруженістю чи індукцією) в обсязі Vдовільної, але достатньої формування інтегральних співвідношень, величини. Виробляючи розподіл обсягу Vна малі обсяги V i, отримаємо вираз

справедливе як загалом, так кожного складового. Перетворимо отриманий вираз таким чином:

(1.7)

і розглянемо межу, до якої прагне вираз у правій частині рівності, укладений у фігурних дужках, при необмеженому розподілі обсягу V. У математиці цю межу називають дивергенцієювектора (у разі вектора електричної індукції D):

Дивергенція вектора Dу декартових координатах:

Таким чином вираз (1.7) перетворюється на вигляд:

.

Враховуючи, що при необмеженому розподілі сума в лівій частині останнього виразу переходить в об'ємний інтеграл, отримаємо

Отримане співвідношення має виконуватися для будь-якого довільно вибраного обсягу V. Це можливо лише в тому випадку, якщо значення підінтегральних функцій у кожній точці простору однакові. Отже, дивергенція вектора Dпов'язана із щільністю заряду в тій же точці рівністю

або для вектора напруженості електростатичного поля

Ці рівності виражають теорему Гауса в диференційної форми.

Зазначимо, що в процесі переходу до диференціальної форми теореми Гауса виходить співвідношення, яке має загальний характер:

.

Вираз називається формулою Гауса - Остроградського та зв'язує інтеграл за обсягом від дивергенції вектора з потоком цього вектора крізь замкнуту поверхню, що обмежує об'єм.

Запитання

1) У чому полягає фізичний сенс теореми Гауса для електростатичного поля у вакуумі

2) У центрі куба знаходиться точковий зарядq. Чому дорівнює потік вектора Е:

а) через повну поверхню куба; б) через одну із граней куба.

Чи зміниться відповіді, якщо:

а) заряд знаходиться не в центрі куба, але всередині його ; б) заряд знаходиться поза кубом.

3) Що таке лінійна, поверхнева, об'ємна щільність заряду.

4) Вкажіть зв'язок об'ємної та поверхневої густини зарядів.

5) Чи може поле поза різноіменно і однорідно заряджених паралельних нескінченних площин бути відмінним від нуля

6) Електричний диполь поміщений усередину замкнутої поверхні. Який потік крізь цю поверхню

Закон взаємодії електричних зарядів – закон Кулона – можна сформулювати інакше, у вигляді так званої теореми Гаусса. Теорема Гауса виходить як наслідок закону Кулона та принципу суперпозиції. Доказ ґрунтується на зворотній пропорційності сили взаємодії двох точкових зарядів квадрату відстані між ними. Тому теорема Гауса застосовна до будь-якого фізичного поля, де діє закон зворотних квадратів і принцип суперпозиції, наприклад гравітаційного поля.

Мал. 9. Лінії напруженості електричного поля точкового заряду, що перетинають замкнуту поверхню X

Щоб сформулювати теорему Гаусса, повернемося до картини силових ліній електричного поля нерухомого точкового заряду. Силові лінії відокремленого точкового заряду є симетрично розташовані радіальні прямі (рис. 7). Можна провести будь-яку кількість таких ліній. Позначимо повне їх число через товщину силових ліній на відстані від заряду, тобто число ліній, що перетинають одиницю поверхні сфери радіуса дорівнює Порівнюючи це співвідношення з виразом для напруженості поля точкового заряду (4), бачимо, що густота ліній пропорційна напруженості поля. Ми можемо зробити ці величини чисельно рівними, належним чином вибравши повну кількість силових ліній N:

Таким чином, поверхня сфери будь-якого радіусу, що охоплює точковий заряд, перетинає те саме число силових ліній. Це означає, що силові лінії безперервні: у проміжку між будь-якими двома концентричними сферами різних радіусів жодна з ліній не обривається і додається жодної нової. Оскільки силові лінії безперервні, така ж кількість силових ліній перетинає будь-яку замкнуту поверхню (рис. 9), що охоплює заряд

Силові лінії мають напрямок. У разі позитивного заряду вони виходять назовні з навколишнього заряду замкнутої поверхні, як показано на рис. 9. У разі негативного заряду вони входять усередину поверхні. Якщо число ліній, що виходять, вважати позитивним, а вхідних - негативним, то у формулі (8) можна опустити знак модуля у заряду і записати її у вигляді

Потік напруженості.Введемо тепер поняття потоку вектора напруженості поля через поверхню. Довільне поле можна подумки розбити на малі області, в яких напруженість змінюється за модулем і напрямом настільки мало, що в межах цієї області поле можна вважати однорідним. У кожній такій області силові лінії є паралельними прямими і мають постійну густоту.

Мал. 10. До визначення потоку вектора напруженості поля через майданчик

Розглянемо, яке число силових ліній пронизує малу майданчик напрямок нормалі до якої утворює кут з напрямком ліній напруженості (рис. 10). Нехай – проекція на площину, перпендикулярну до силових ліній. Так як число ліній, що перетинають однаково, а густота ліній, згідно з прийнятою умовою, дорівнює модулю напруженості поля Е, то

Величина а є проекцією вектора Е на напрямок нормалі до майданчика

Тому кількість силових ліній, що перетинають майданчик, дорівнює

Твір носить назву потоку напруженості поля через поверхню Формула (10) показує, що потік вектора через поверхню дорівнює числу силових ліній, що перетинають цю поверхню. Зазначимо, що потік вектора напруженості, як і кількість силових ліній, що проходять через поверхню, є скаляр.

Мал. 11. Потік вектора напруженості Е через майданчик

Залежність потоку від орієнтації майданчика щодо силових ліній ілюструється на рис.

Потік напруженості поля через довільну поверхню є сумою потоків через елементарні майданчики, на які можна розбити цю поверхню. В силу співвідношень (9) і (10) можна стверджувати, що потік напруженості поля точкового заряду через будь-яку охоплюючу заряд замкнуту поверхню 2 (див. рис. 9), як число силових ліній, що виходять з цієї поверхні, дорівнює При цьому вектор нормалі до елементарних майданчиків замкнутої поверхні слід спрямовувати назовні. Якщо заряд усередині поверхні від'ємний, то силові лінії входять всередину цієї поверхні і пов'язаний із зарядом потік вектора напруженості поля також негативний.

Якщо всередині замкнутої поверхні знаходиться кілька зарядів, то відповідно до принципу суперпозиції будуть складатися потоки напруженості їх полів. Повний потік дорівнюватиме де під слід розуміти алгебраїчну суму всіх зарядів, що знаходяться всередині поверхні.

Якщо всередині замкнутої поверхні електричних зарядів немає або їх сума алгебри дорівнює нулю, то повний потік напруженості поля через цю поверхню дорівнює нулю: скільки силових ліній входить в об'єм, обмежений поверхнею, стільки ж і виходить назовні.

Тепер можна остаточно сформулювати теорему Гауса: потік вектора напруженості електричного поля Е у вакуумі через будь-яку замкнуту поверхню пропорційний повному заряду, що знаходиться всередині цієї поверхні. Математично теорема Гаусса виражається тією ж формулою (9), де розуміється алгебраїчна сума зарядів. В абсолютній електростатичній

системі одиниць СГСЕ коефіцієнт та теорема Гауса записується у вигляді

У СІ та потік напруженості через замкнуту поверхню виражається формулою

Теорема Гауса широко використовується в електростатиці. У деяких випадках з її допомогою легко розраховуються поля, які створюються симетрично розташованими зарядами.

Поля симетричних джерел.Застосуємо теорему Гаусса до розрахунку напруженості електричного поля рівномірно зарядженого на поверхні кулі радіуса . Будемо для визначеності вважати його заряд позитивним. Розподіл зарядів, що створюють поле, має сферичну симетрію. Тому таку ж симетрію має і поле. Силові лінії такого поля спрямовані по радіусах, а модуль напруженості однаковий у всіх точках, що рівно віддалені від центру кулі.

Для того, щоб знайти напруженість поля на відстані від центру кулі, проведемо подумки концентричну з кулею сферичну поверхню радіусу.

Але цю величину можна висловити за допомогою теореми Гаусса. Якщо нас цікавить поле поза кулею, тобто при тому, наприклад, у СІ і, порівнюючи з (13), знаходимо

У системі одиниць СДСЕ, очевидно,

Таким чином, зовні кулі напруженість поля така сама, як у поля точкового заряду поміщеного в центр кулі. Якщо ж цікавитися полем усередині кулі, тобто при тому, що весь розподілений по поверхні кулі заряд перебуває поза мисленно проведеною нами сферою. Тому поле всередині кулі відсутнє:

Аналогічно за допомогою теореми Гауса можна розрахувати електростатичне поле, створюване нескінченною зарядженою

площиною із щільністю постійної у всіх точках площині. З міркувань симетрії вважатимуться, що силові лінії перпендикулярні площині, спрямовані від неї обидві сторони і мають всюди однакову густоту. Дійсно, якби густота силових ліній у різних точках була різною, то переміщення зарядженої площини вздовж самої себе призводило б до зміни поля у цих точках, що суперечить симетрії системи – такий зсув не повинен змінювати поле. Іншими словами, поле нескінченної рівномірно зарядженої площини є однорідним.

Як замкнута поверхня для застосування теореми Гауса виберемо поверхню циліндра, побудованого таким чином: утворююча циліндра паралельна силовим лініям, а основи мають площі паралельні зарядженій площині і лежать по різні боки від неї (рис. 12). Потік напруженості поля через бічну поверхню дорівнює нулю, тому повний потік через замкнуту поверхню дорівнює сумі потоків через основи циліндра:

Мал. 12. До обчислення напруженості поля рівномірно зарядженої площини

По теоремі Гаусса цей же потік визначається зарядом тієї частини площини, яка лежить всередині циліндра, і СІ дорівнює Порівнюючи ці вирази для потоку, знаходимо

У системі СГСЕ напруженість поля рівномірно зарядженої нескінченної площини дається формулою

Для рівномірно зарядженої пластини кінцевих розмірів отримані вирази приблизно справедливі в області, що знаходиться досить далеко від країв пластини і не далеко від її поверхні. Поблизу країв пластини поле не буде однорідним і його силові лінії викривляються. На дуже великих порівняно з розмірами пластини відстанях поле зменшується з відстанню так само, як поле точкового заряду.

Як інші приклади полів, створюваних симетрично розподіленими джерелами, можна навести поле рівномірно зарядженої по довжині нескінченної прямолінійної нитки, поле рівномірно зарядженого нескінченного кругового циліндра, поле кулі,

рівномірно зарядженого за обсягом і т. п. Теорема Гауса дозволяє у всіх цих випадках легко розраховувати напруженість поля.

Теорема Гаусса дає зв'язок між полем та його джерелами, у певному сенсі зворотний той, що дає закон Кулона, який дозволяє визначити електричне поле за заданими зарядами. За допомогою теореми Гауса можна визначити сумарний заряд у будь-якій області простору, в якій відомий розподіл електричного поля.

У чому відмінність концепцій далекодії та близькодії при описі взаємодії електричних зарядів? Якою мірою ці концепції можна застосувати до гравітаційної взаємодії?

Що таке напруга електричного поля? Що мають на увазі, коли її називають силовою характеристикою електричного поля?

Яким чином по картині силових ліній можна судити про напрям і модуль напруженості поля в певній точці?

Чи можуть силові лінії електричного поля перетинатись? Аргументуйте свою відповідь.

Намалюйте якісну картину силових ліній електростатичного поля двох таких зарядів, що .

Потік напруженості електричного поля через замкнуту поверхню виражається різними формулами (11) і (12) у системах одиниць ГСЕ та СІ. Як це пов'язати з геометричним змістом потоку, що визначається числом силових ліній, що перетинають поверхню?

Як використовувати теорему Гауса для знаходження напруженості електричного поля при симетричному розподілі зарядів, що його створюють?

Як застосувати формули (14) та (15) до обчислення напруженості поля кулі з негативним зарядом?

Теорема Гауса та геометрія фізичного простору.Подивимося на доказ теореми Гауса з дещо іншого погляду. Повернемося до формули (7), з якої було зроблено висновок про те, що через будь-яку навколишню заряд сферичну поверхню проходить те саме число силових ліній. Цей висновок пов'язані з тим, що відбувається скорочення знаменниках обох частин рівності.

У правій частині виникло через те, що сила взаємодії зарядів, що описується законом Кулона, обернено пропорційна квадрату відстані між зарядами. У лівій частині поява пов'язана з геометрією: площа поверхні сфери пропорційна квадрату її радіусу.

Пропорційність площі поверхні квадрату лінійних розмірів – це відмінна риса евклідової геометрії у тривимірному просторі. Дійсно, пропорційність площ саме квадратам лінійних розмірів, а не будь-якого іншого цілого ступеня, характерна для простору

трьох вимірів. Те, що цей показник ступеня дорівнює точно двом, а чи не відрізняється від двійки хай навіть у мізерно малу величину, свідчить про невикривленості цього тривимірного простору, т. е. у тому, що його геометрія саме евклідова.

Таким чином, теорема Гауса – це прояв властивостей фізичного простору у фундаментальному законі взаємодії електричних зарядів.

Ідея про тісний зв'язок фундаментальних законів фізики з властивостями простору висловлювалася багатьма визначними розумами ще задовго до встановлення самих цих законів. Так, І. Кант за три десятиліття до відкриття закону Кулона писав про властивості простору: «Тримірність відбувається, мабуть, тому, що субстанції в існуючому світі діють одна на одну таким чином, що сила дії обернено пропорційна квадрату відстані».

Закон Кулона і теорема Гауса фактично представляють той самий закон природи, виражений у різних формах. Закон Кулона відбиває концепцію далекодії, тоді як теорема Гаусса виходить з уявлення про силове поле, що заповнює простір, тобто з концепції близькодії. В електростатиці джерелом силового поля є заряд, і пов'язана з джерелом характеристика поля – потік напруженості – не може змінитися у порожньому просторі, де немає інших зарядів. Оскільки потік можна наочно уявляти як сукупність силових ліній поля, то незмінність потоку проявляється у безперервності цих ліній.

Теорема Гаусса, заснована на зворотній пропорційності взаємодії квадрату відстані і принципі суперпозиції (адитивності взаємодії), застосовна до будь-якого фізичного поля, у якому діє закон зворотних квадратів. Зокрема вона справедлива і для гравітаційного поля. Зрозуміло, що це не просто випадковий збіг, а відображення того, що і електрична, і гравітаційна взаємодія розігруються у тривимірному фізичному евклідовому просторі.

На якій особливості закону взаємодії електричних зарядів ґрунтується теорема Гауса?

Доведіть, ґрунтуючись на теоремі Гауса, що напруженість електричного поля точкового заряду обернено пропорційна квадрату відстані. Які властивості симетрії простору використовуються у цьому доказі?

Як геометрія фізичного простору відбивається у законі Кулона і теоремі Гаусса? Яка особливість цих законів свідчить про евклідовий характер геометрії та тривимірності фізичного простору?

Загальне формулювання: Потік вектора напруженості електричного поля через будь-яку, довільно вибрану замкнуту поверхню пропорційний ув'язненому в цій поверхні електричному заряду.

У системі СДСЕ:

У системі СІ:

- Потік вектора напруженості електричного поля через замкнуту поверхню.

- Повний заряд, що міститься в об'ємі, який обмежує поверхню.

- Електрична постійна.

Даний вираз є теоремою Гауса в інтегральній формі.

У диференціальній формі теорема Гауса відповідає одному з рівнянь Максвелла і виражається так

у системі СІ:

,

у системі СДСЕ:

Тут об'ємна щільність заряду (у разі присутності середовища сумарна щільність вільних і пов'язаних зарядів), а оператор набла.

Для теореми Гауса справедлив принцип суперпозиції, тобто потік вектора напруженості через поверхню не залежить від розподілу заряду всередині поверхні.

Фізичною основою теореми Гауса є закон Кулона або, інакше, теорема Гауса є інтегральним формулюванням закону Кулона.

Теорема Гауса для електричної індукції (електричне усунення).

Для поля в речовині електростатична теорема Гауса може бути записана інакше через потік вектора електричного зміщення (електричної індукції). При цьому формулювання теореми виглядає наступним чином: потік вектора електричного зміщення через замкнуту поверхню пропорційний ув'язненому в цій поверхні вільному електричному заряду:

Якщо ж розглядати теорему для напруженості поля в речовині, то як заряд Q необхідно брати суму вільного заряду, що знаходиться всередині поверхні і поляризаційного (індукованого, пов'язаного) заряду діелектрика:

,

де ,
- Вектор поляризації діелектрика.

Теорема Гауса для магнітної індукції

Потік вектора магнітної індукції через будь-яку замкнуту поверхню дорівнює нулю:

.

Це еквівалентно з того що у природі немає «магнітних зарядів» (монополів), які створювали б магнітне полі, як електричні заряди створюють електричне полі. Іншими словами, теорема Гауса для магнітної індукції показує, що магнітне поле є вихровим.

Застосування теореми Гауса

Для обчислення електромагнітних полів використовуються такі величини:

Об'ємна щільність заряду (див. вище).

Поверхнева щільність заряду

де dS - нескінченно мала ділянка поверхні.

Лінійна щільність заряду

де dl - Довжина нескінченно малого відрізка.

Розглянемо поле, створюване нескінченною однорідною зарядженою площиною. Нехай поверхнева густина заряду площини однакова і дорівнює σ. Уявімо подумки циліндр з утворюючими, перпендикулярними до площини, і основою S, розташованим щодо площини симетрично. У силу симетрії. Потік вектора напруженості дорівнює. Застосувавши теорему Гауса, отримаємо:

,

з котрого

у системі СДСЕ

Важливо відзначити, що незважаючи на свою універсальність та спільність, теорема Гауса в інтегральній формі має порівняно обмежене застосування через незручність обчислення інтегралу. Однак у разі симетричної задачі рішення її стає набагато простішим, ніж з використанням принципу суперпозиції.