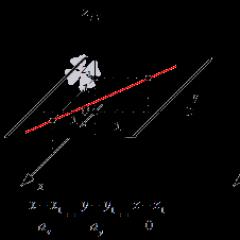
Рівняння прямої в просторі - це рівняння двох площин, що перетинаються. Канонічне та параметричне рівняння прямої Як написати канонічне рівняння прямої

Одним із видів рівнянь прямий у просторі є канонічне рівняння. Ми розглянемо це поняття у всіх подробицях, оскільки знати його необхідно для вирішення багатьох практичних завдань.

У першому пункті ми сформулюємо основні рівняння прямої, розташованої у тривимірному просторі, та наведемо кілька прикладів. Далі покажемо способи обчислення координат напрямного вектора при заданих рівняннях канонічних і рішення зворотної задачі. У третій частині ми розповімо, як складається рівняння прямої, що проходить через 2 задані точки в тривимірному просторі, а в останньому пункті вкажемо на зв'язку канонічних рівнянь з іншими. Усі міркування будуть проілюстровані прикладами розв'язання завдань.

Про те, що взагалі є канонічні рівняння прямої, ми вже говорили в статті, присвяченій рівнянням прямої на площині. Випадок із тривимірним простором ми розберемо за аналогією.

Припустимо, ми маємо прямокутну систему координат O x y z , у якій задана пряма. Як ми пам'ятаємо, поставити пряму можна у різний спосіб. Використовуємо найпростіший з них – задаємо точку, через яку проходитиме пряма, і вкажемо напрямний вектор. Якщо позначити пряму буквою a , а точку M , можна записати, що M 1 (x 1 , y 1 , z 1) лежить на прямій a і напрямним вектором цієї прямої буде a → = (a x , a y , a z) . Щоб безліч точок M (x , y , z) визначало пряму a вектори M 1 M → і a → повинні бути колінеарними,

Якщо ми знаємо координати векторів M 1 M → і a → , то можемо записати в координатній формі необхідну та достатню умову їхньої колінеарності. З початкових умов нам вже відомі координати a → . Для того щоб отримати координати M 1 M → нам необхідно обчислити різницю між M (x , y , z) і M 1 (x 1 , y 1 , z 1) . Запишемо:

M 1 M → = x - x 1 , y - y 1 , z - z 1

Після цього потрібну умову ми можемо сформулювати так: M 1 M → = x - x 1 , y - y 1 , z - z 1 і a → = (a x , a y , a z) : M 1 M → = λ · a → ⇔ x - x 1 = λ · a x y - y 1 = λ · a y z - z 1 = λ · a z

Тут значенням змінної може бути будь-яке дійсне число або нуль. Якщо ?

При значеннях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 ми можемо розв'язати щодо параметра λ усі рівняння системи x - x 1 = λ · a x y - y 1 = λ · a y z - z 1 = λ · a z

Між правими частинами після цього можна буде поставити знак рівності:

x - x 1 = λ · a x y - y 1 = λ · a y z - z 1 = λ · a z ⇔ λ = x - x 1 a x λ = y - y 1 a y λ = z - z 1 a z ⇔ x - x 1 a x = y - y 1 a y = z - z 1 a z

У результаті ми отримали рівняння x - x 1 a x = y - y 1 a y = z - z 1 a z , з допомогою яких можна визначити пряму в тривимірному просторі. Це і потрібні нам канонічні рівняння.

Такий запис використовується навіть при нульових значеннях одного або двох параметрів a x , a y , a z , оскільки він у цих випадках він також буде вірним. Усі три параметри не можуть дорівнювати 0 , оскільки напрямний вектор a → = (a x , a y , a z) нульовим не буває.

Якщо один-два параметри a дорівнюють 0, то рівняння x - x 1 a x = y - y 1 a y = z - z 1 a z носить умовний характер. Його слід вважати рівним наступного запису:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ, λ ∈ R.

Окремі випадки канонічних рівнянь ми розберемо у третьому пункті статті.

З визначення канонічного рівняння прямої у просторі можна зробити кілька важливих висновків. Розглянемо їх.

1) якщо вихідна пряма проходитиме через дві точки M 1 (x 1 , y 1 , z 1) і M 2 (x 2 , y 2 , z 2) , то канонічні рівняння набудуть наступного вигляду:

x - x 1 a x = y - y 1 a y = z - z 1 a z або x - x 2 a x = y - y 2 a y = z - z 2 a z.

2) оскільки a → = (a x , a y , a z) є напрямним вектором вихідної прямої, то такими будуть і всі вектори μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тоді пряма може бути визначена за допомогою рівняння x - x 1 a x = y - y 1 a y = z - z 1 a z або x - x 1 μ · a x = y - y 1 μ · a y = z - z 1 μ · a z.

Ось кілька прикладів таких рівнянь із заданими значеннями:

Приклад 1 Приклад 2

Як скласти канонічне рівняння прямої в просторі

Ми з'ясували, що канонічні рівняння виду x - x 1 a x = y - y 1 a y = z - z 1 a z будуть відповідати прямій через точку M 1 (x 1 , y 1 , z 1) , а вектор a → = ( a x , a y , a z) буде для неї напрямним. Отже, якщо ми знаємо рівняння прямої, то можемо обчислити координати її напрямного вектора, а за умови заданих координат вектора та деякої точки, розташованої на прямій, ми можемо записати її канонічні рівняння.

Розберемо кілька конкретних завдань.

Приклад 3

Ми маємо пряму, задану в тривимірному просторі за допомогою рівняння x + 1 4 = y 2 = z - 3 - 5 . Запишіть координати всіх напрямних векторів для неї.

Рішення

Щоб отримати координати напрямного вектора, нам треба просто взяти значення знаменників із рівняння. Ми отримаємо, що одним із напрямних векторів буде a → = (4 , 2 , - 5) , а безліч усіх подібних векторів можна сформулювати як μ · a → = 4 · μ , 2 · μ , - 5 · μ . Тут параметр μ – будь-яке дійсне число (за винятком нуля).

Відповідь: 4 · μ , 2 · μ , - 5 · μ , μ ∈ R , μ ≠ 0

Приклад 4

Запишіть канонічні рівняння, якщо пряма у просторі проходить через M 1 (0 , - 3 , 2) та має напрямний вектор з координатами - 1 , 0 , 5 .

Рішення

У нас є дані, що x 1 = 0, y 1 = - 3, z 1 = 2, a x = - 1, a y = 0, a z = 5. Цього цілком достатньо, щоб одразу перейти до запису канонічних рівнянь.

Зробимо це:

x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ x - 0 - 1 = y - (- 3) 0 = z - 2 5 ⇔ ⇔ x - 1 = y + 3 0 = z - 2 5

Відповідь: x - 1 = y + 3 0 = z - 2 5

Ці завдання – найпростіші, тому що в них є всі або майже всі вихідні дані для запису рівняння чи координат вектора. Насправді частіше можна зустріти ті, у яких спочатку потрібно шукати потрібні координати, та був записувати канонічні рівняння. Приклади таких завдань ми розбирали у статтях, присвячених знаходженню рівнянь прямої, що проходить через точку простору паралельно заданої, а також прямої, що проходить через деяку точку простору перпендикулярно до площини.

Раніше ми вже говорили, що одне-два значення параметрів a x, a y, a z в рівняннях можуть мати нульові значення. При цьому запис x - x 1 a x = y - y 1 a y = z - z 1 a z = λ набуває формального характеру, оскільки ми отримуємо один або два дроби з нульовими знаменниками. Її можна переписати у наступному вигляді (при λ ∈ R):

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Розглянемо ці випадки докладніше. Припустимо, що a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , або a x ≠ 0 , a y ≠ 0 , a z = 0 . У такому разі потрібні рівняння ми можемо записати так:

1. В першому випадку:
   x - x 1 0 = y - y 1 a y = z - z 1 a z = λ ⇔ x - x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x - x 1 = 0 y - y 1 a y = z - z 1 a z = λ

У другому випадку:
x - x 1 a x = y - y 1 0 = z - z 1 a z = λ ⇔ x = x 1 + a x · λ y - y 1 = 0 z = z 1 + a z · λ ⇔ y - y 1 = 0 x - x 1 a x = z - z 1 a z = λ

У третьому випадку:
x - x 1 a x = y - y 1 a y = z - z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z - z 1 = 0 ⇔ z - z 1 = 0 x - x 1 a x = y - y 1 a y = λ

Виходить, що при такому значенні параметрів потрібні прямі знаходяться в площинах x - x 1 = 0, y - y 1 = 0 або z - z 1 = 0, які розташовуються паралельно координатним площинам (якщо x 1 = 0, y 1 = 0 або z1 = 0). Приклади таких прямих показано на ілюстрації.

Отже, ми зможемо записати канонічні рівняння трохи інакше.

1. У першому випадку: x - x 1 0 = y - y 1 0 = z - z 1 a z = λ ⇔ x - x 1 = 0 y - y 1 = 0 z = z 1 + a z · λ , λ ∈ R
2. У другому: x - x 1 0 = y - y 1 a y = z - z 1 0 = ?
3. У третьому: x - x 1 a x = y - y 1 0 = z - z 1 0 = ?

У всіх трьох випадках вихідні прямі збігатимуться з координатними осями або виявляться паралельними ним: x 1 = 0 y 1 = 0, x 1 = 0 z 1 = 0, y 1 = 0 z 1 = 0 . Їхні напрямні вектори мають координати 0, 0, a z, 0, a y, 0, a x, 0, 0. Якщо позначити напрямні вектори координатних прямих як i → j → k → , то напрямні вектори заданих прямих будуть колінеарними по відношенню до них. На малюнку показані такі випадки:

На прикладах, як застосовуються ці правила.

Приклад 5

Знайдіть канонічні рівняння, за допомогою яких можна визначити у просторі координатні прямі O z , O x , O y .

Рішення

Координатні вектори i → = (1, 0, 0), j → = 0, 1, 0, k → = (0, 0, 1) будуть для вихідних прямих напрямними. Також ми знаємо, що наші прямі обов'язково проходитимуть через точку O(0, 0, 0), оскільки вона є початком координат. Тепер ми маємо всі дані, щоб записати потрібні канонічні рівняння.

Для прямої O x: x 1 = y 0 = z 0

Для прямої O y: x 0 = y 1 = z 0

Для прямої O z : x 0 = y 0 = z 1

Відповідь: x 1 = y 0 = z 0 x 0 = y 1 = z 0 x 0 = y 0 = z 1 .

Приклад 6

У просторі задана пряма, яка проходить через точку M 1 (3 - 1 12) . Також відомо, що вона розташована паралельно до осі ординат. Запишіть канонічні рівняння цієї прямої.

Рішення

З огляду на умову паралельності ми можемо сказати, що вектор j → = 0 , 1 , 0 буде для потрібної прямої напрямної. Отже, шукані рівняння матимуть вигляд:

x - 3 0 = y - (- 1) 1 = z - 12 0 ⇔ x - 3 0 = y + 1 1 = z - 12 0

Відповідь: x - 3 0 = y + 1 1 = z - 12 0

Припустимо, що у нас є дві точки M 1 (x 1 , y 1 , z 1) і M 2 (x 2 , y 2 , z 2) , через які проходить пряма. Як ми можемо сформулювати для неї канонічне рівняння?

Для початку приймемо вектор M 1 M 2 → (або M 2 M 1 →) за напрямний вектор цієї прямої. Оскільки у нас є координати потрібних точок, одразу обчислюємо координати вектора:

M 1 M 2 → = x 2 - x 1 , y 2 - y 1 , z 2 - z 1

x - x 1 x 2 - x 1 = y - y 1 y 2 - y 1 = z - z 1 z 2 - z 1 x - x 2 x 2 - x 1 = y - y 2 y 2 - y 1 = z - z 2 z 2 - z 1

Рівності, що вийшли - це і є канонічні рівняння прямої, що проходить через дві задані точки. Погляньте на ілюстрацію:

Наведемо приклад розв'язання задачі.

Приклад 7

у просторі є дві точки з координатами M 1 (-2, 4, 1) і M 2 (-3, 2, - 5), через які проходить пряма. Запишіть канонічні рівняння для неї.

Рішення

Відповідно до умов, x 1 = - 2, y 1 = - 4, z 1 = 1, x 2 = - 3, y 2 = 2, z 2 = - 5. Нам потрібно підставити ці значення у канонічне рівняння:

x - (- 2) - 3 - (- 2) = y - (- 4) 2 - (- 4) = z - 1 - 5 - 1 ⇔ x + 2 - 1 = y + 4 6 = z - 1 - 6

Якщо ми візьмемо рівняння виду x - x 2 x 2 - x 1 = y - y 2 y 2 - y 1 = z - z 2 z 2 - z 1 то у нас вийде: x - (- 3) - 3 - ( - 2) = y - 2 2 - (- 4) = z - (- 5) - 5 - 1 ⇔ x + 3 - 1 = y - 2 6 = z + 5 - 6

Відповідь: x + 3 - 1 = y - 2 6 = z + 5 - 6 чи x + 3 - 1 = y - 2 6 = z + 5 - 6 .

Перетворення канонічних рівнянь прямої в просторі на інші види рівнянь

Іноді користуватися канонічними рівняннями виду x – x 1 a x = y – y 1 a y = z – z 1 a z не дуже зручно. Для вирішення деяких завдань краще використовувати запис x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ. У деяких випадках краще визначити потрібну пряму за допомогою рівнянь двох площин, що перетинаються A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Тому в даному пункті ми розберемо, як можна перейти від канонічних рівнянь до інших видів, якщо це потрібно за умовами завдання.

Зрозуміти правила переходу до параметричних рівнянь нескладно. Спочатку прирівняємо кожну частину рівняння до параметра і дозволимо ці рівняння щодо інших змінних. У результаті отримаємо:

x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ ⇔ x - x 1 a x = λ y - y 1 a y = λ z - z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Значення параметра може бути будь-яким дійсним числом, адже і x , y , z можуть приймати будь-які дійсні значення.

Приклад 8

У прямокутній системі координат у тривимірному просторі задана пряма, яка визначена рівнянням x - 23 = y - 2 = z + 70. Запишіть канонічне рівняння у параметричному вигляді.

Рішення

Спочатку прирівнюємо кожну частину дробу до λ.

x - 2 3 = y - 2 = z + 7 0 ⇔ x - 2 3 = λ y - 2 = λ z + ​​7 0 = λ

Тепер дозволяємо першу частину щодо x, другу – щодо y, третю – щодо z. У нас вийде:

x - 2 3 = λ y - 2 = λ z + ​​7 0 = λ ⇔ x = 2 + 3 · λ y = - 2 · λ z = - 7 + 0 · λ ⇔ x = 2 + 3 · λ y = - 2 · λ z = - 7

Відповідь: x = 2 + 3 · λ y = - 2 · λ z = - 7

Наступним нашим кроком буде перетворення канонічних рівнянь на рівняння двох площин, що перетинаються (для однієї і тієї ж прямої).

Рівність x - x 1 a x = y - y 1 a y = z - z 1 a z потрібно для початку подати у вигляді системи рівнянь:

x - x 1 a x = y - y 1 a y x - x 1 a x = z - z 1 a x y - y 1 a y = z - z 1 a z

Оскільки p q = r s ми розуміємо як p · s = q · r то можна записати:

x - x 1 a x = y - y 1 a y x - x 1 a x = z - z 1 a z y - y 1 a y = z - z 1 a z ⇔ a y · (x - x 1) = a x · (y - y 1) a z · (x - x 1) = a x · (z - z 1) a z · (y - y 1) = a y · (z - z 1) ⇔ ⇔ a y · x - a x · y + a x · y 1 - a y · x 1 = 0 a z · x - a x · z + a x · z 1 - a z · x 1 = 0 a z · y - a y · z + a y · z 1 - a z · y 1 = 0

У результаті в нас вийшло, що:

x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ a y · x - a x · y + a x · y 1 - a y · x 1 = 0 a z · x - a x · z + a x · z 1 - a z · x 1 = 0 a z · y - a y · z + a y · z 1 - a z · y 1 = 0

Вище ми зазначали, що це три параметра a можуть одночасно бути нульовими. Значить, ранг основної матриці системи дорівнюватиме 2 , оскільки a y - a x 0 a z 0 - a x 0 a z - a y = 0 і один з визначників другого порядку не дорівнює 0:

a y - a x a z 0 = a x · a z , a y 0 a z - a x = a x · a y , - a x 0 0 - a x = a x 2 a y - a x 0 a z = a y · a z , a y 0 0 - a y = - a y 2 , - a x 0 a z - a y = a x · a y z 0 0 a z = a z 2 , a z - a x 0 - a y = - a y · a z , 0 - a x a z - a y = a x · a z

Це дає можливість виключити одне рівняння з наших розрахунків. Таким чином, канонічні рівняння прямої можна перетворити на систему з двох лінійних рівнянь, які будуть містити 3 невідомі. Вони і будуть потрібними нам рівняннями двох площин, що перетинаються.

Міркування виглядає досить складним, проте практично все робиться досить швидко. Продемонструємо це з прикладу.

Приклад 9

Пряма задана канонічним рівнянням x - 12 = y0 = z + 20. Напишіть для неї рівняння площин, що перетинаються.

Рішення

Почнемо з попарного прирівнювання дробів.

x - 1 2 = y 0 = z + 2 0 ⇔ x - 1 2 = y 0 x - 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · (x - 1) = 2 y 0 · (x - 1) = 2 · (z + 2) 0 · y = 0 · (z + 2) ⇔ y = 0 z + 2 = 0 0 = 0

Тепер виключаємо з розрахунків останнє рівняння, тому що воно буде вірним за будь-яких x , y і z . У такому разі x - 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0.

Це і є рівняння двох площин, що перетинаються, які при перетині утворюють пряму, задану за допомогою рівняння x - 1 2 = y 0 = z + 2 0

Відповідь: y = 0 z + 2 = 0

Приклад 10

Пряма задана рівняннями x + 1 2 = y - 2 1 = z - 5 - 3 знайдіть рівняння двох площин, що перетинаються по даній прямій.

Рішення

Прирівнюємо дроби попарно.

x + 1 2 = y - 2 1 = z - 5 - 3 ⇔ x + 1 2 = y - 2 1 x + 1 2 = z - 5 - 3 y - 2 1 = z - 5 - 3 ⇔ ⇔ 1 · ( x + 1) = 2 · (y - 2) - 3 · (x + 1) = 2 · (z - 5) - 3 · (y - 2) = 1 · (z - 5) ⇔ x - 2 y + 5 = 0 3 x + 2 z - 7 = 0 3 y + 7 - 11 = 0

Отримуємо, що визначник основної матриці отриманої системи дорівнюватиме 0:

1 - 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + (-2) · 2 · 0 + 0 · 3 · 3 - 0 · 0 · 0 - 1 · 2 · 3 - (- 2) · 3 · 1 = 0

Мінор другого порядку нульовим у своїй нічого очікувати: 1 - 2 3 0 = 1 · 0 - (- 2) · 3 = 6 . Тоді ми можемо прийняти його як базисний мінор.

Через війну ми можемо обчислити ранг основний матриці системи x - 2 y + 5 = 0 3 x + 2 z - 7 = 0 3 y + z - 11 = 0 . Це буде 2. Третє рівняння виключаємо з розрахунку та отримуємо:

x - 2 y + 5 = 0 3 x + 2 z - 7 = 0 3 y + z - 11 = 0 ⇔ x - 2 y + 5 = 0 3 x + 2 z - 7 = 0

Відповідь: x - 2 y + 5 = 0 3 x + 2 z - 7 = 0

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Розглянемо рішення прикладу.

приклад.

Знайдіть координати будь-якої точки прямої, заданої в просторі рівняннями двох площин, що перетинаються. .

Рішення.

Перепишемо систему рівнянь у такому вигляді

Як базисний мінор основної матриці системи візьмемо відмінний від нуля мінор другого порядку , тобто, z – вільна невідома змінна. Перенесемо доданки, що містять z у праві частини рівнянь: .

Приймемо , де - довільне дійсне число, тоді .

Розв'яжемо отриману систему рівнянь:

Таким чином, загальне рішення системи рівнянь має вигляд, де.

Якщо взяти конкретне значення параметра , ми отримаємо приватне рішення системи рівнянь, яке дає шукані координати точки, що лежить заданої прямої. Візьмемо тоді , Отже, - шукана точка прямий.

Можна виконати перевірку знайдених координат точки, підставивши їх у вихідні рівняння двох площин, що перетинаються:

Відповідь:

Напрямний вектор прямий, якою перетинаються дві площини.

У прямокутній системі координат від прямої лінії невіддільний напрямний вектор прямої. Коли пряма а прямокутної системі координат в тривимірному просторі задана рівняннями двох перетинаються площин і , то координати напрямного вектора прямої не видно. Нині ми покажемо, як їх визначати.

Ми знаємо, що пряма перпендикулярна до площини, коли вона перпендикулярна до будь-якої прямої, що лежить у цій площині. Тоді нормальний вектор площини перпендикулярний будь-якому ненульовому вектору, що лежить у цій площині. Цими фактами і скористаємося при знаходженні напрямного вектора прямої.

Пряма а лежить як і площині , і у площині . Отже, напрямний вектор прямий перпендикулярний і нормальному вектору площині і нормальному вектору площині. Таким чином, напрямним вектором прямої а є і :

Безліч всіх напрямних векторів прямий а ми можемо поставити як де - параметр, що приймає будь-які дійсні значення, відмінні від нуля.

приклад.

Знайдіть координати будь-якого напрямного вектора прямої, яка задана в прямокутній системі координат Oxyz у тривимірному просторі рівняннями двох площин, що перетинаються. .

Рішення.

Нормальними векторами площин і є вектори і відповідно. Напрямний вектор прямої, що є перетином двох заданих площин, приймемо векторний добуток нормальних векторів:

Відповідь:

Перехід до параметричних та канонічних рівнянь прямий у просторі.

Бувають випадки, в яких використання рівнянь двох площин, що перетинаються, для опису прямої не зовсім зручно. Деякі завдання простіше вирішуються, якщо відомі канонічні рівняння прямої у просторі виду або параметричні рівняння прямої у просторі виду , де x 1 , y 1 , z 1 - координати деякої точки прямої, a x , a y , a z - координати напрямного вектора прямої, а - параметр, що приймає довільні дійсні значення. Опишемо процес переходу від рівнянь прямого вигляду до канонічних та параметричних рівнянь прямої у просторі.

У попередніх пунктах ми навчилися знаходити координати деякої точки прямої, а також координати деякого напрямного вектора прямої, яка задана рівняннями двох площин, що перетинаються. Цих даних достатньо, щоб записати і канонічні та параметричні рівняння цієї прямої у прямокутній системі координат у просторі.

Розглянемо рішення прикладу, а потім покажемо ще один спосіб знаходження канонічних і параметричних рівнянь прямої в просторі.

приклад.

Рішення.

Обчислимо спочатку координати напрямного вектора прямої. Для цього знайдемо векторне твір нормальних векторів і площин і :

Тобто, .

Тепер визначимо координати деякої точки заданої прямої. Для цього знайдемо одне із рішень системи рівнянь .

Визначник відмінний від нуля, візьмемо його як базовий мінор основної матриці системи. Тоді змінна z є вільною, переносимо доданки з нею в праві частини рівнянь, і надаємо змінної z довільне значення:

Вирішуємо методом Крамера отриману систему рівнянь:

Отже,

Приймемо, при цьому отримуємо координати точки прямої: .

Тепер ми можемо записати необхідні канонічні та параметричні рівняння вихідної прямої у просторі:

Відповідь:

і

Ось другий спосіб вирішення цього завдання.

При знаходженні координат певної точки прямої ми розв'язуємо систему рівнянь . Загалом її рішення можна записати у вигляді .

А це якраз шукані параметричні рівняння прямої в просторі. Якщо кожне з отриманих рівнянь дозволити щодо параметра і після цього прирівняти праві частини рівностей, то отримаємо канонічні рівняння прямої в просторі

Покажемо розв'язання попередньої задачі за цим методом.

приклад.

Пряма в тривимірному просторі задана рівняннями двох площин, що перетинаються. . Напишіть канонічні та параметричні рівняння цієї прямої.

Рішення.

Вирішуємо цю систему із двох рівнянь із трьома невідомими (рішення наведено в попередньому прикладі, не повторюватимемося). При цьому отримуємо . Це і шукані параметричні рівняння прямої в просторі.

Залишилося отримати канонічні рівняння прямої у просторі:

Отримані рівняння прямої зовні відрізняються від рівнянь, отриманих у попередньому прикладі, проте вони еквівалентні, так як визначають одну і ту ж множину точок тривимірного простору (а значить, одну і ту ж пряму).

Відповідь:

і

Список літератури.

• Бугров Я.С., Микільський С.М. Вища математика. Том перший: елементи лінійної алгебри та аналітичної геометрії.
• Ільїн В.А., Позняк Е.Г. Аналітична геометрія.

Як скласти рівняння прямої у просторі?

Рівняння прямий у просторі

Аналогічно «плоский» прямий, є кілька способів, якими ми можемо поставити пряму у просторі. Почнемо з канонів – точки та напрямного вектора прямої:

Якщо відома деяка точка простору, що належить прямий, і напрямний вектор даної прямої, то канонічні рівняння цієї прямої виражаються формулами:

Наведений запис передбачає, що координати напрямного вектора не дорівнюють нулю. Що робити, якщо одна чи дві координати нульові, ми розглянемо трохи згодом.

Як і у статті Рівняння площиниДля простоти вважатимемо, що у всіх завданнях уроку дії проводяться в ортонормованому базисі простору.

Приклад 1

Скласти канонічні рівняння прямої по точці та напрямному вектору

Рішення: Канонічні рівняння прямої складемо за формулою:

Відповідь:

І їжу зрозуміло… хоча, ні, їжу не зрозуміло взагалі нічого.

Що слід зазначити у цьому дуже простому прикладі? По-перше, отримані рівняння НЕ ТРЕБА скорочувати на одиницю: . Скоротити, точніше, можна, але це незвично ріже око і створює незручності під час вирішення завдань.

А по-друге, в аналітичній геометрії неминучі дві речі – це перевірка та залік:

Про всяк випадок дивимося на знаменники рівнянь і звіряємось – чи правильнотам записані координати напрямного вектора. Ні, не подумайте, у нас не урок у дитячому садочку «Гальмошка». Ця порада дуже важлива, оскільки дозволяє повністю виключити помилку через неуважність. Ніхто не застрахований, а раптом неправильно переписали? Нагородять премією Дарвіна з геометрії.

Отримано вірні рівності, отже, координати точки задовольняють нашим рівнянням, і сама точка дійсно належить даній прямій.

Перевірка дуже легко (і швидко!) виконується усно.

У ряді завдань потрібно знайти якусь іншу точку, що належить даній прямій. Як це зробити?

Беремо отримані рівняння і подумки «відщипуємо», наприклад, лівий шматочок: . Тепер цей шматочок прирівнюємо до будь-якого числа(Пам'ятаємо, що нуль вже був), наприклад, до одиниці: . Так як , то і два інших «шматки» теж повинні дорівнювати одиниці. По суті, потрібно вирішити систему:

Перевіримо, чи задовольняє знайдена точка рівнянням :

Отримані вірні рівності, отже, точка дійсно лежить на цій прямій.

Виконаємо креслення у прямокутній системі координат. Заодно згадаємо, як правильно відкладати крапки у просторі:

Будуємо точку:
- Від початку координат в негативному напрямку осі відкладаємо відрізок першої координати (зелений пунктир);
- Друга координата нульова, тому «не смикаємося» з осі ні вліво, ні вправо;
– у відповідність до третьої координати відміряємо три одиниці вгору (фіолетовий пунктир).

Будуємо точку: відміряємо дві одиниці «на себе» (жовтий пунктир), одну одиницю вправо (синій пунктир) та дві одиниці вниз (коричневий пунктир). Коричневий пунктир і сама точка наклалися на координатну вісь, зверніть увагу, що вони знаходяться в нижньому півпросторі та перед віссю .

Сама пряма проходить над віссю і, якщо мене не підводить окомір, над віссю. Не підводить, переконався аналітично. Якби пряма проходила ЗА віссю, то слід би стерти гумкою частинку лінії зверху і знизу точки схрещування.

У прямий нескінченно багато напрямних векторів, наприклад:
(червона стрілка)

Вийшов точно вихідний вектор , але це чиста випадковість, таку вже я вибрав точку . Усі напрямні вектори прямої колінеарні, та його відповідні координати пропорційні (детальніше – див. Лінійна (не) залежність векторів. Базис векторів). Так, вектори теж будуть напрямними векторами цієї прямої.

Додаткову інформацію про побудову тривимірних креслень на папері можна знайти на початку методички Графіки та властивості функцій. У зошиті різнокольорові пунктирні доріжки до точок зазвичай тонко прокреслюють простим олівцем тим же пунктиром.

Розберемося з окремими випадками, коли одна або дві координати напрямного вектора нульові. Попутно продовжуємо тренування просторового зору, яке почалося на початку уроку Рівняння площини. І знову я розповім вам казку про голого короля – намалюю порожню систему координат і переконуватиму вас, що там є просторові прямі =)

Простіше перерахувати всі шість випадків:

1) Для точки та напрямного вектора канонічні рівняння прямої розпадаються на три окремихрівняння: .

Або коротше:

Приклад 2: складемо рівняння прямої по точці та напрямному вектору :

Що то за пряма? Напрямний вектор прямий колінеарен орту, отже, дана пряма буде паралельна осі. Канонічні рівняння слід розуміти так:
а) – «гравець» та «зет» постійні, рівні конкретним числам;
б) змінна «ікс» може набувати будь-яких значень: (на практиці дане рівняння, як правило, не записують).

Зокрема, рівняння задають саму вісь. Справді, «ікс» набуває будь-якого значення, а «ігрок» і «зет» завжди дорівнюють нулю.

Розглянуті рівняння можна інтерпретувати й іншим чином: подивимося, наприклад, на аналітичний запис осі абсцис: . Адже це рівняння двох площин! Рівняння задає координатну площину, а рівняння – координатну площину. Правильно думаєте – ці координатні площини перетинаються по осі. Спосіб, коли пряма у просторі задається перетином двох площин, ми розглянемо наприкінці уроку.

Два схожі випадки:

2) Канонічні рівняння прямої, що проходить через точку паралельно вектору, виражаються формулами.

Такі прямі будуть паралельні координатній осі. Зокрема, рівняння задають координатну саму вісь ординат.

3) Канонічні рівняння прямої, що проходить через точку паралельно вектору, виражаються формулами.

Дані прямі паралельні координатній осі, а рівняння задають саму вісь аплікат.

Заженемо в стійло другу трійку:

4) Для точки та напрямного вектора канонічні рівняння прямої розпадаються на пропорцію і рівняння площини .

Приклад 3: складемо рівняння прямої по точці та напрямному вектору.

Канонічні рівняння прямої

Постановка задачі. Знайти канонічні рівняння прямої, заданої як лінія перетину двох площин (загальними рівняннями)

План розв'язання. Канонічні рівняння прямої з напрямним вектором , що проходить через цю точку , мають вигляд

. (1)

Тому, щоб написати канонічні рівняння прямої, необхідно знайти її напрямний вектор і якусь точку на прямій.

1. Оскільки пряма належить одночасно обом площинам, її напрямний вектор ортогонален нормальним векторам обох площин, тобто. згідно з визначенням векторного твору, маємо

. (2)

2. Вибираємо якусь точку на прямій. Оскільки напрямний вектор прямий паралельний хоча б однієї з координатних площин, то пряма перетинає цю координатну площину. Отже, як точка на прямій може бути взята точка її перетину з цією координатною площиною.

3. Підставляємо знайдені координати напрямного вектора та точки в канонічні рівняння прямої (1).

Зауваження. Якщо векторний добуток (2) дорівнює нулю, то площини не перетинаються (паралельні) і записати канонічні рівняння прямої неможливо.

Завдання 12.Написати канонічні рівняння прямої.

Канонічні рівняння прямої:

,

де – координати будь-якої точки прямої, – її напрямний вектор.

Знайдемо якусь точку прямої. Нехай тоді

Отже, - Координати точки, що належить прямий.

КУТ між площинами

Розглянемо дві площини α 1 і α 2 задані відповідно рівняннями:

Під кутомміж двома площинами розумітимемо один із двогранних кутів, утворених цими площинами. Очевидно, що кут між нормальними векторами і площин 1 і 2 дорівнює одному із зазначених суміжних двогранних кутів або . Тому . Т.к. і , то

.

приклад.Визначити кут між площинами x+2y-3z+4=0 та 2 x+3y+z+8=0.

Умови паралельності двох площин.

Дві площини α 1 і α 2 паралельні тоді і тільки тоді, коли їх нормальні вектори і паралельні, а отже .

Отже, дві площини паралельні один одному тоді і лише тоді, коли коефіцієнти за відповідних координат пропорційні:

або

Умови перпендикулярності площин.

Зрозуміло, що дві площини перпендикулярні і тоді, коли їх нормальні вектори перпендикулярні, отже, або .

Таким чином, .

приклади.

ПРЯМА В ПРОСТОРІ.

ВЕКТОРНЕ РІВНЯННЯ ПРЯМОЮ.

ПАРАМЕТРИЧНІ РІВНЯННЯ ПРЯМИЙ

Положення прямий у просторі цілком визначається завданням якоїсь її фіксованої точки М 1 і вектор , паралельний цій прямій.

Вектор , паралельний прямий, називається напрямнимвектор прямий.

Отже, хай пряма lпроходить через точку М 1 (x 1 , y 1 , z 1), що лежить на прямій паралельно вектору.

Розглянемо довільну точку М(x, y, z)на прямий. З малюнка видно, що .

Вектори та колінеарні, тому знайдеться таке число t, що , де множник tможе набувати будь-яке числове значення в залежності від положення точки Mна прямий. Множник tназивається параметром. Позначивши радіус-вектори точок М 1 і Мвідповідно через і, отримуємо. Це рівняння називається векторнимрівнянням прямої. Воно показує, що кожному значення параметра tвідповідає радіус-вектор деякої точки М, що лежить на прямий.

Запишемо це рівняння у координатній формі. Зауважимо, що , і звідси

Отримані рівняння називаються параметричнимирівняннями прямий.

При зміні параметра tзмінюються координати x, yі zі крапка Мпереміщається прямою.

КАНОНІЧНІ РІВНЯННЯ ПРЯМИЙ

Нехай М 1 (x 1 , y 1 , z 1) - точка, що лежить на прямій l, і - Її напрямний вектор. Знову візьмемо на пряму довільну точку М(x, y, z)і розглянемо вектор.

Зрозуміло, що вектори та колінеарні, тому їх відповідні координати мають бути пропорційними, отже,

– канонічнірівняння прямої.

Зауваження 1.Зауважимо, що канонічні рівняння прямої можна було отримати з параметричних, виключивши параметр t. Справді, з параметричних рівнянь отримуємо або .

приклад.Записати рівняння прямої у параметричному вигляді.

Позначимо , звідси x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Примітка 2.Нехай пряма перпендикулярна до однієї з координатних осей, наприклад осі Ox. Тоді напрямний вектор прямий перпендикулярний Ox, отже, m=0. Отже, параметричні рівняння прямий набудуть вигляду

Виключаючи з рівнянь параметр t, Отримаємо рівняння прямий у вигляді

Проте й у разі умовимося формально записувати канонічні рівняння прямої як . Таким чином, якщо в знаменнику одного з дробів стоїть нуль, то це означає, що пряма перпендикулярна до відповідної координатної осі.

Аналогічно, канонічним рівнянням відповідає пряма перпендикулярна до осей Oxі Ойабо паралельна осі Oz.

приклади.

ЗАГАЛЬНІ РІВНЯННЯ ПРЯМОГО, ЯК ЛІНІЇ ПЕРЕРОСИННЯ ДВОХ ПЛОЩИН

Через кожну пряму в просторі проходить безліч площин. Будь-які дві з них, перетинаючи, визначають її у просторі. Отже, рівняння будь-яких двох таких площин, що розглядаються спільно, являють собою рівняння цієї прямої.

Взагалі будь-які дві не паралельні площини, задані загальними рівняннями

визначають пряму їх перетину. Ці рівняння називаються загальними рівняннямипрямий.

приклади.

Побудувати пряму, задану рівняннями

Для побудови прямої достатньо знайти будь-які її точки. Найпростіше вибрати точки перетину прямої з координатними площинами. Наприклад, точку перетину з площиною xOyотримаємо з рівнянь прямий, вважаючи z= 0:

Вирішивши цю систему, знайдемо точку M 1 (1;2;0).

Аналогічно, вважаючи y= 0, отримаємо точку перетину прямої з площиною xOz:

Від загальних рівнянь прямої можна перейти до її канонічних або параметричних рівнянь. Для цього потрібно знайти якусь точку М 1 на прямий та напрямний вектор прямий.

Координати точки М 1 отримаємо з цієї системи рівнянь, надавши одній з координат довільне значення. Для пошуку напрямного вектора, зауважимо, що цей вектор має бути перпендикулярним до обох нормальних векторів. і . Тому за напрямний вектор прямий lможна взяти векторний добуток нормальних векторів:

.

приклад.Привести загальні рівняння прямої до канонічного вигляду.

Знайдемо точку, що лежить на прямій. Для цього виберемо довільно одну з координат, наприклад, y= 0 і розв'яжемо систему рівнянь:

Нормальні вектори площин, що визначають пряму, мають координати. Тому напрямний вектор прямий буде

. Отже, l: .

КУТ МІЖ ПРЯМИМИ

Кутомміж прямими в просторі будемо називати будь-який із суміжних кутів, утворених двома прямими, проведеними через довільну точку паралельно даним.

Нехай у просторі задані дві прямі:

Очевидно, що за кут між прямими можна прийняти кут між їх напрямними векторами і . Так як , то за формулою для косинуса кута між векторами отримаємо