اعمال اولین حد قابل توجه. اولین حد قابل توجه: نظریه و مثال ها

محدودیت های شگفت انگیز را پیدا کنیدنه تنها برای بسیاری از دانش آموزان سال اول و دوم تحصیلی که تئوری حدود را مطالعه می کنند، بلکه برای برخی از معلمان نیز دشوار است.

فرمول اولین حد قابل توجه

پیامدهای اولین حد قابل توجه فرمول ها را بنویسید
1. 2. 3. 4. اما به خودی خود، فرمول های کلی حدود قابل توجه به کسی در یک امتحان یا آزمون کمک نمی کند. نکته اصلی این است که وظایف واقعی به گونه‌ای ساخته می‌شوند که فرمول‌های نوشته شده در بالا هنوز نیاز به دستیابی دارند. و اکثر دانش‌آموزانی که کلاس‌ها را رها می‌کنند، این درس را به صورت مکاتبه‌ای مطالعه می‌کنند یا معلمانی دارند که خودشان همیشه نمی‌دانند درباره چه چیزی توضیح می‌دهند، نمی‌توانند ابتدایی‌ترین مثال‌ها را تا حد قابل توجه محاسبه کنند. از فرمول های اولین حد قابل توجه، می بینیم که می توان از آنها برای بررسی عدم قطعیت هایی مانند صفر تقسیم بر صفر برای عبارات با توابع مثلثاتی استفاده کرد. ابتدا تعدادی مثال را در مورد اول در نظر بگیرید حد فوق العاده y، و سپس دومین حد قابل توجه را مطالعه خواهیم کرد.

مثال 1. حد تابع sin(7*x)/(5*x) را بیابید.
راه حل: همانطور که می بینید، تابع زیر حد به اولین حد قابل توجه نزدیک است، اما حد خود تابع قطعا برابر با یک نیست. در چنین تخصیصی به حدود، باید در مخرج متغیری با همان ضریب موجود در متغیر زیر سینوس مشخص شود. در این صورت تقسیم و ضرب در 7 کنید

برای برخی، چنین جزئیاتی اضافی به نظر می رسد، اما برای بسیاری از دانش آموزانی که برای آنها محدودیت قائل نیستند، به درک بهتر قوانین و یادگیری مطالب نظری کمک می کند.
همچنین اگر وجود داشته باشد نمای معکوستوابع نیز اولین محدودیت قابل توجه است. و همه به این دلیل که حد شگفت انگیز برابر با یک است

همین قانون در مورد پیامدهای 1 حد قابل توجه نیز صدق می کند. بنابراین، اگر از شما بپرسند "اولین حد شگفت انگیز چیست؟" شما باید بدون تردید پاسخ دهید که یک واحد است.

مثال 2. حد تابع sin(6x)/tan(11x) را بیابید.
راه حل: برای فهمیدن نتیجه نهایی تابع را در فرم می نویسیم

برای اعمال قوانین حد قابل توجه ضرب و تقسیم بر عوامل

در ادامه حد حاصلضرب توابع را بر حسب حاصلضرب حد می نویسیم

بدون فرمول های پیچیده، حد چند تابع مثلثاتی را پیدا کردیم. برای جذب فرمول های سادهسعی کنید حد 2 و 4 را پیدا کنید، فرمول نتیجه 1 از حد فوق العاده. ما وظایف پیچیده تری را در نظر خواهیم گرفت.

مثال 3. حد (1-cos(x))/x^2 را محاسبه کنید
راه حل: هنگام بررسی با تعویض، عدم قطعیت 0/0 را دریافت می کنیم. بسیاری نمی دانند چگونه چنین مثالی را به 1 حد شگفت انگیز کاهش دهند. در اینجا باید از فرمول مثلثاتی استفاده کنید

در این صورت حد به شکل واضح تبدیل می شود

ما موفق شده ایم تابع را به مربع یک حد قابل توجه کاهش دهیم.

مثال 4. حد را پیدا کنید
راه حل: هنگام جایگزینی، ویژگی آشنا 0/0 را دریافت می کنیم. با این حال، متغیر به پی نزدیک می شود، نه به صفر. بنابراین، برای اعمال اولین حد قابل توجه، چنین تغییری را در متغیر x انجام می دهیم، به طوری که متغیر جدید به صفر می رسد. برای انجام این کار، مخرج را به عنوان متغیر جدید Pi-x=y نشان می دهیم

بنابراین، با استفاده از فرمول مثلثاتی، که در کار قبلی داده شده است، مثال به 1 حد قابل توجه کاهش می یابد.

مثال 5 محاسبه حد
راه حل: در ابتدا مشخص نیست که چگونه می توان محدودیت ها را ساده کرد. اما اگر مثالی وجود دارد، پس باید پاسخ داده شود. این واقعیت که متغیر به واحد می رود، هنگام جایگزینی، یک تکینگی از شکل صفر ضرب در بی نهایت می دهد، بنابراین مماس باید با فرمول جایگزین شود.

پس از آن، عدم قطعیت مورد نظر 0/0 را بدست می آوریم. در مرحله بعد، تغییر متغیرها را در حد انجام می دهیم و از تناوب کوتانژانت استفاده می کنیم

آخرین تعویض‌ها به ما امکان می‌دهد از نتیجه 1 از حد قابل توجه استفاده کنیم.

دومین حد قابل توجه برابر با توان است

این یک کلاسیک است که در مشکلات واقعی همیشه رسیدن به محدودیت ها آسان نیست.
برای محاسبات شما نیاز دارید محدودیت ها پیامدهای دومین حد قابل توجه است:
1. 2. 3. 4.
به لطف دومین حد قابل توجه و پیامدهای آن، می توان عدم قطعیت هایی مانند صفر تقسیم بر صفر، یک به توان بی نهایت و بی نهایت تقسیم بر بی نهایت و حتی به همان درجه را بررسی کرد.

بیایید با چند مثال ساده شروع کنیم.

مثال 6 حد یک تابع را پیدا کنید
راه حل: به طور مستقیم اعمال 2 محدودیت فوق العاده کار نخواهد کرد. ابتدا باید نشانگر را بچرخانید تا شکل آن برعکس عبارت داخل پرانتز باشد

این تکنیک کاهش به 2 حد قابل توجه و در واقع اشتقاق فرمول 2 پیامد حد است.

مثال 7 حد یک تابع را پیدا کنید
راه حل: ما برای فرمول 3 نتیجه 2 حد قابل توجه وظایف داریم. جایگزینی صفر تکینگی به شکل 0/0 می دهد. برای بالا بردن حد زیر قانون، مخرج را می‌چرخانیم تا متغیر ضریب مشابهی در لگاریتم داشته باشد.

همچنین درک و اجرای آن در امتحان آسان است. مشکلات دانش آموزان در محاسبه حدود با کارهای زیر شروع می شود.

مثال 8 محاسبه حد تابع[(x+7)/(x-3)]^(x-2)
راه حل: یک تکینگی از نوع 1 به توان بی نهایت داریم. اگر من را باور ندارید، می توانید بی نهایت را به جای "x" در همه جا جایگزین کنید و خودتان ببینید. برای افزایش بر اساس قانون، صورت را بر مخرج داخل پرانتز تقسیم می کنیم، برای این کار ابتدا دستکاری ها را انجام می دهیم.

عبارت را با حد جایگزین کنید و آن را به 2 حد فوق العاده تبدیل کنید

حد، توان 10 است. ثابت‌هایی که هم در پرانتز و هم در درجه دارای یک متغیر هستند، هیچ "آب و هوا" ندارند - این را باید به خاطر داشت. و اگر معلمان از شما بپرسند - "چرا نشانگر را نمی چرخانید؟" (برای این مثال در x-3)، سپس بگویید که "وقتی متغیری به سمت بی نهایت میل می کند، سپس 100 را به آن اضافه کنید، یا 1000 را کم کنید، و حد ثابت می ماند!".
راه دومی برای محاسبه محدودیت های این نوع وجود دارد. در کار بعدی در مورد آن صحبت خواهیم کرد.

مثال 9 حد را پیدا کنید
راه حل: حالا متغیر را در صورت و مخرج خارج می کنیم و یک ویژگی را به ویژگی دیگر تبدیل می کنیم. برای بدست آوردن مقدار نهایی از فرمول نتیجه 2 حد قابل توجه استفاده می کنیم

مثال 10 حد یک تابع را پیدا کنید
راه حل: همه نمی توانند حد تعیین شده را پیدا کنند. برای افزایش حد به 2، تصور کنید که sin (3x) یک متغیر است و شما باید توان را بچرخانید.

سپس اندیکاتور را به صورت درجه در یک درجه می نویسیم

آرگومان های میانی در پرانتز توضیح داده شده اند. در نتیجه استفاده از حد فوق العاده اول و دوم، به توان مکعبی رسیدیم.

مثال 11. محاسبه حد تابع sin(2*x)/log(3*x+1)
راه حل: ما یک عدم قطعیت از فرم 0/0 داریم. علاوه بر این، می بینیم که تابع باید به استفاده از هر دو محدودیت فوق العاده تبدیل شود. اجازه دهید تبدیل های ریاضی قبلی را انجام دهیم

علاوه بر این، بدون مشکل، محدودیت مقدار را می گیرد

اگر یاد بگیرید که چگونه به سرعت توابع را رنگ آمیزی کنید و آنها را به اولین یا دومین حد فوق العاده کاهش دهید، به این ترتیب در تست ها، تست ها، ماژول ها احساس راحتی خواهید کرد. اگر به خاطر سپردن روش های بالا برای یافتن محدودیت برای شما دشوار است، همیشه می توانید سفارش دهید تستبه محدودیت های ما
برای انجام این کار، فرم را پر کنید، داده ها را مشخص کنید و یک فایل را با مثال ضمیمه کنید. ما به دانش آموزان زیادی کمک کرده ایم - ما نیز می توانیم به شما کمک کنیم!

اولین حد قابل توجه اغلب برای محاسبه حدهای حاوی سینوس، آرکسین، مماس، مماس قوس و عدم قطعیت های حاصل از تقسیم بر صفر استفاده می شود.

فرمول

فرمول اولین محدودیت قابل توجه این است: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$

متوجه شدیم که $ \alpha\to 0 $ $ \sin\alpha \ به 0 $ را به دست می‌دهد، بنابراین در صورت و مخرج صفر داریم. بنابراین، فرمول اولین حد قابل توجه برای آشکار کردن عدم قطعیت های $ \frac(0)(0) $ مورد نیاز است.

برای اعمال فرمول، دو شرط باید رعایت شود:

عبارات موجود در سینوس و مخرج کسری یکسان است
عبارات در سینوس و مخرج کسری به صفر تمایل دارند

توجه! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ اگرچه عبارات زیر سینوس و مخرج یکسان هستند، اما $ 2x ^2+1 = 1 $، وقتی $ x\ تا 0 $. شرط دوم برآورده نمی شود، بنابراین فرمول نمی تواند اعمال شود!

عواقب

به ندرت، در کارها می توانید یک حد اول و شگفت انگیز را ببینید که در آن می توانید بلافاصله پاسخ را یادداشت کنید. در عمل، همه چیز کمی پیچیده تر به نظر می رسد، اما برای چنین مواردی دانستن عواقب اولین محدودیت قابل توجه مفید خواهد بود. با تشکر از آنها، می توانید به سرعت محدودیت های مورد نظر را محاسبه کنید.

$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$

$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$

نمونه های راه حل

اجازه دهید اولین حد قابل توجه را در نظر بگیریم، مثال هایی از راه حل آن برای محاسبه حدودهای حاوی توابع مثلثاتی و عدم قطعیت $ \bigg[\frac(0)(0)\bigg] $

مثال 1
محاسبه $ \lim_(x\to 0) \frac(\sin2x)(4x) $
راه حل
حد را در نظر بگیرید و توجه داشته باشید که حاوی سینوس است. بعد، $ x = 0 $ را به صورت و مخرج جایگزین می کنیم و عدم قطعیت صفر تقسیم بر صفر را بدست می آوریم: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)( 0) $$ قبلاً دو علامت وجود دارد که شما باید یک حد فوق العاده اعمال کنید، اما یک تفاوت ظریف وجود دارد: ما نمی توانیم فوراً فرمول را اعمال کنیم، زیرا عبارت زیر علامت سینوس با عبارت در مخرج متفاوت است. و ما به برابری آنها نیاز داریم. بنابراین، با کمک تحولات ابتداییصورتگر آن را به $2x$ تبدیل می کنیم. برای انجام این کار، دوس را از مخرج کسری با یک عامل جداگانه خارج می کنیم. به نظر می رسد: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ , که در پایان $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ با فرمول بدست آمد. اگر نمی توانید مشکل خود را حل کنید، آن را برای ما ارسال کنید. ما تهیه خواهیم کرد راه حل دقیق. شما می توانید با پیشرفت محاسبات آشنا شوید و اطلاعات را جمع آوری کنید. این به شما کمک می کند تا به موقع از معلم امتیاز بگیرید!
پاسخ
$$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$

مثال 2
$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ را پیدا کنید
راه حل
مثل همیشه، ابتدا باید نوع عدم قطعیت را بدانید. اگر صفر بر صفر تقسیم شود، به وجود یک سینوس توجه می کنیم: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ این عدم قطعیت به ما امکان می دهد از فرمول اولین حد قابل توجه استفاده کنیم، اما عبارت مخرج برابر با آرگومان سینوس نیست؟ بنابراین، استفاده از فرمول "روی پیشانی" غیرممکن است. باید کسر را ضرب و تقسیم بر آرگومان سینوسی کنید: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x-x^ 4)(x ^3+2x)) = $$ اکنون ویژگی های محدودیت ها را شرح می دهیم: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x-x^4 )\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ حد دوم فقط با فرمول مطابقت دارد و برابر است با یک: $ $ = \lim_(x\to 0) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x)(2x- x^4) = $$ دوباره $ x = 0 $ را به کسری جایگزین کنید و عدم قطعیت $ \frac(0)(0) $ را بدست آورید. برای حذف آن کافی است که $ x $ را از پرانتز خارج کنید و با آن کاهش دهید: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2)(2) = 1 $$
پاسخ
$$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$

مثال 4
محاسبه $ \lim_(x\to0) \frac(\sin2x)(tg3x) $
راه حل
بیایید محاسبه را با جایگزینی $ x=0 $ شروع کنیم. در نتیجه، عدم قطعیت $ \frac(0)(0) $ را دریافت می کنیم. حد شامل یک سینوس و یک مماس است که با استفاده از فرمول اولین حد قابل توجه به توسعه احتمالی وضعیت اشاره می کند. بیایید صورت و مخرج کسر را به فرمول و نتیجه تبدیل کنیم: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ اکنون می بینیم که در صورت و مخرج عباراتی مناسب برای فرمول و پیامدها وجود دارد. آرگومان سینوسی و آرگومان مماس برای مخرج های مربوطه یکسان هستند $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$
پاسخ
$$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$

در مقاله: "نخستین حد قابل توجه، نمونه هایی از راه حل ها" در مورد مواردی که استفاده از این فرمول توصیه می شود و پیامدهای آن گفته شد.

از مقاله بالا، می توانید دریابید که محدودیت چیست و با چه چیزی خورده می شود - این بسیار مهم است. چرا؟ ممکن است متوجه نشوید که تعیین کننده ها چیست و آنها را با موفقیت حل کنید، ممکن است اصلاً درک نکنید که مشتق چیست و آنها را روی "پنج" بیابید. اما اگر نمی دانید محدودیت چیست، حل وظایف عملی دشوار خواهد بود. همچنین، آشنایی با نمونه های طراحی تصمیمات و توصیه های من برای طراحی اضافی نخواهد بود. تمام اطلاعات به روشی ساده و در دسترس ارائه شده است.

و برای اهداف این درس به مواد روش شناختی زیر نیاز داریم: محدودیت های قابل توجهو فرمول های مثلثاتی. آنها را می توان در صفحه پیدا کرد. بهتر است کتابچه ها را چاپ کنید - بسیار راحت تر است، علاوه بر این، اغلب باید به صورت آفلاین به آنها دسترسی داشت.

چه چیزی در مورد محدودیت های شگفت انگیز قابل توجه است؟ قابل توجه بودن این محدودیت ها در این واقعیت نهفته است که آنها توسط بزرگترین ذهن های ریاضیدانان مشهور اثبات شده اند و فرزندان سپاسگزار مجبور نیستند از محدودیت های وحشتناکی با انبوهی از توابع مثلثاتی، لگاریتم ها و درجات رنج ببرند. یعنی در زمان یافتن حدود از نتایج آماده ای که به صورت تئوری ثابت شده است استفاده می کنیم.

چندین محدودیت قابل توجه وجود دارد، اما در عمل، دانشجویان پاره وقت در 95٪ موارد دارای دو محدودیت قابل توجه هستند: اولین حد فوق العاده, دومین حد فوق العاده. لازم به ذکر است که اینها اسامی تثبیت شده تاریخی هستند و وقتی مثلاً از "نخستین حد قابل توجه" صحبت می کنند ، منظور آنها یک چیز کاملاً خاص است و نه محدودیت تصادفی از سقف.

اولین حد فوق العاده

محدودیت زیر را در نظر بگیرید: (به جای حرف بومی "او" استفاده خواهم کرد نامه یونانی"آلفا"، از نظر ارائه مطالب راحت تر است).

طبق قانون ما برای یافتن محدودیت ها (به مقاله مراجعه کنید محدودیت ها نمونه های راه حل) سعی می کنیم صفر را جایگزین تابع کنیم: در صورت حساب صفر می شود (سینوس صفر صفر است)، در مخرج، بدیهی است که نیز صفر است. بنابراین ما با نامشخصی شکل مواجه هستیم که خوشبختانه نیازی به افشای آن نیست. میدانم تجزیه و تحلیل ریاضی، ثابت می شود که:

این واقعیت ریاضی نامیده می شود اولین حد فوق العاده. من یک مدرک تحلیلی از حد ارائه نمی کنم، اما اینجاست معنی هندسیبیایید نگاهی به درس بیندازیم توابع بی نهایت کوچک.

اغلب در کارهای عملی، عملکردها را می توان متفاوت ترتیب داد، این چیزی را تغییر نمی دهد:

- همان حد فوق العاده اول.

اما شما نمی توانید صورت و مخرج را دوباره مرتب کنید! اگر محدودیتی در فرم داده شده باشد، باید به همان شکل حل شود، بدون اینکه چیزی دوباره تنظیم شود.

در عمل، نه تنها یک متغیر می تواند به عنوان یک پارامتر عمل کند، بلکه یک تابع ابتدایی نیز می باشد. تابع پیچیده. فقط مهم است که به سمت صفر گرایش داشته باشد.

مثال ها:
, , ,

اینجا ، ، ، ، و همه چیز وزوز است - اولین محدودیت فوق العاده قابل اجرا است.

و اینجا مدخل بعدی است - بدعت:

چرا؟ از آنجا که چند جمله ای به صفر تمایل ندارد، به پنج میل می کند.

اتفاقاً سوال برای پرکردن است، اما حد آن چیست ? پاسخ را می توان در انتهای درس یافت.

در عمل، همه چیز آنقدر هموار نیست، تقریباً هرگز به دانش آموزی پیشنهاد نمی شود که یک محدودیت رایگان را حل کند و یک اعتبار آسان دریافت کند. هوم... من دارم این سطرها را می نویسم و یک فکر بسیار مهم به ذهنم خطور کرد - از این گذشته، به نظر می رسد بهتر است تعاریف و فرمول های ریاضی "رایگان" را به خاطر بسپارید، این می تواند کمک ارزشمندی در آزمون باشد، زمانی که موضوع بین "دو" و "سه" تصمیم گیری می شود و معلم تصمیم می گیرد از دانش آموز چند سوال ساده یا پیشنهاد حل کند. ساده ترین مثال(«شاید او (الف) هنوز چه چیزی را بداند؟!»).

بیایید به بررسی ادامه دهیم نمونه های عملی:

مثال 1

حد را پیدا کنید

اگر متوجه یک سینوس در حد شدیم، باید بلافاصله ما را به فکر کردن در مورد امکان اعمال اولین حد قابل توجه بیندیشیم.

ابتدا سعی می کنیم 0 را در عبارت زیر علامت حد جایگزین کنیم (این کار را به صورت ذهنی یا پیش نویس انجام می دهیم):

بنابراین، ما یک نامعین بودن شکل، آن داریم حتما نشان دهیددر تصمیم گیری عبارت زیر علامت حد به نظر اولین حد فوق العاده است، اما این کاملاً نیست، زیر سینوس است، اما در مخرج است.

در چنین مواردی، ما باید اولین محدودیت فوق العاده را خودمان با استفاده از یک دستگاه مصنوعی سازماندهی کنیم. خط استدلال می تواند به شرح زیر باشد: "تحت سینوس ما، به این معنی که ما نیز باید در مخرج وارد شویم".
و این کار بسیار ساده انجام می شود:

یعنی مخرج به طور مصنوعی در این مورد در 7 ضرب و بر همان هفت تقسیم می شود. حالا رکورد شکلی آشنا به خود گرفته است.
هنگامی که کار با دست ترسیم می شود، توصیه می شود اولین محدودیت قابل توجه را مشخص کنید با یک مداد ساده:

چی شد؟ در واقع عبارت دایره ای به یک واحد تبدیل شده و در محصول ناپدید شده است:

اکنون فقط برای خلاص شدن از کسری سه طبقه باقی مانده است:

چه کسی ساده سازی کسرهای چند طبقه را فراموش کرده است، لطفا مطالب را در کتاب مرجع تجدید کنید. فرمول های ریاضی مدرسه داغ .

آماده. جواب نهایی:

اگر نمی خواهید از علامت های مداد استفاده کنید، راه حل را می توان به شکل زیر قالب بندی کرد:

“

ما از اولین محدودیت قابل توجه استفاده می کنیم

“

مثال 2

حد را پیدا کنید

باز هم کسری و سینوس را در حد می بینیم. سعی می کنیم صفر را در صورت و مخرج جایگزین کنیم:

در واقع، ما دچار عدم قطعیت هستیم و بنابراین، باید سعی کنیم اولین حد قابل توجه را سازماندهی کنیم. روی درس محدودیت ها نمونه های راه حلما این قاعده را در نظر گرفتیم که وقتی عدم قطعیت داریم، باید صورت و مخرج را به عامل تبدیل کنیم. در اینجا - همان چیز، ما درجات را به عنوان یک محصول (ضریب) ارائه می دهیم:

مشابه مثال قبلی، ما با یک مداد محدودیت های شگفت انگیز را ترسیم می کنیم (در اینجا دو مورد از آنها وجود دارد)، و نشان می دهیم که آنها به یکی تمایل دارند:

در واقع، پاسخ آماده است:

در مثال‌های زیر، من در Paint هنر انجام نمی‌دهم، فکر می‌کنم چگونه یک راه‌حل را به درستی در یک نوت بوک ترسیم کنم - قبلاً متوجه شده‌اید.

مثال 3

حد را پیدا کنید

صفر را در عبارت زیر علامت حد جایگزین می کنیم:

یک عدم قطعیت به دست آمده است که باید افشا شود. اگر یک مماس در حد وجود داشته باشد، تقریباً همیشه طبق فرمول مثلثاتی شناخته شده به سینوس و کسینوس تبدیل می شود (به هر حال، آنها تقریباً همین کار را با کوتانژانت انجام می دهند، در زیر ببینید). مواد روشمند داغ فرمول های مثلثاتی در صفحه فرمول های ریاضی، جداول و مواد مرجع).

در این مورد:

کسینوس صفر برابر با یک است و خلاص شدن از شر آن آسان است (فراموش نکنید که علامت بزنید که به یک تمایل دارد):

بنابراین، اگر کسینوس در حد یک ضرب باشد، به طور کلی، باید به یک واحد تبدیل شود که در محصول ناپدید می شود.

در اینجا همه چیز ساده تر شد، بدون هیچ ضرب و تقسیم. اولین محدودیت قابل توجه نیز به وحدت تبدیل می شود و در محصول ناپدید می شود:

در نتیجه بی نهایت حاصل می شود، اتفاق می افتد.

مثال 4

حد را پیدا کنید

سعی می کنیم صفر را در صورت و مخرج جایگزین کنیم:

عدم قطعیت به دست آمده (کسینوس صفر، همانطور که به یاد داریم، برابر با یک است)

از فرمول مثلثاتی استفاده می کنیم. یادداشت بردار! به دلایلی، محدودیت های استفاده از این فرمول بسیار رایج است.

ضریب های ثابت را فراتر از نماد حد خارج می کنیم:

بیایید اولین محدودیت قابل توجه را سازماندهی کنیم:

در اینجا ما فقط یک محدودیت فوق العاده داریم که به یک تبدیل می شود و در محصول ناپدید می شود:

بیایید از شر سه طبقه خلاص شویم:

حد در واقع حل شده است، ما نشان می دهیم که سینوس باقی مانده به صفر میل دارد:

مثال 5

حد را پیدا کنید

این مثال پیچیده تر است، سعی کنید خودتان آن را بفهمید:

برخی از محدودیت ها را می توان با تغییر متغیر به اولین حد قابل توجه کاهش داد، می توانید در این مورد کمی بعد در مقاله بخوانید. روش های حل محدودیت.

دومین حد فوق العاده

در تئوری تحلیل ریاضی ثابت شده است که:

این واقعیت نامیده می شود دومین محدودیت قابل توجه.

ارجاع: یک عدد غیر منطقی است

نه تنها یک متغیر می تواند به عنوان یک پارامتر عمل کند، بلکه یک تابع پیچیده است. فقط مهم این است که برای بی نهایت تلاش کند.

مثال 6

حد را پیدا کنید

هنگامی که عبارت زیر علامت حد در قدرت است - این اولین علامتی است که باید سعی کنید دومین حد فوق العاده را اعمال کنید.

اما اول، مثل همیشه، سعی می کنیم بی پایان جایگزین کنیم عدد بزرگدر بیان اینکه با چه اصل این کار انجام می شود، در درس مورد تجزیه و تحلیل قرار گرفت محدودیت ها نمونه های راه حل.

به راحتی می توان فهمید که چه زمانی پایه درجه و توان - ، یعنی عدم قطعیت شکل وجود دارد:

این عدم قطعیت فقط با کمک دومین حد قابل توجه آشکار می شود. اما، همانطور که اغلب اتفاق می افتد، دومین حد شگفت انگیز روی یک بشقاب نقره قرار ندارد و باید به طور مصنوعی سازماندهی شود. شما می توانید به صورت زیر دلیل کنید: در این مثال، پارامتر به این معنی است که ما نیز باید در اندیکاتور سازماندهی کنیم. برای این کار، پایه را به یک پاور می‌بریم و برای اینکه عبارت تغییر نکند، آن را به یک پاور می‌رسانیم:

وقتی کار با دست ترسیم می شود، با مداد علامت می زنیم:

تقریباً همه چیز آماده است، درجه وحشتناک به یک نامه زیبا تبدیل شده است:

در همان زمان، خود نماد حد به نشانگر منتقل می شود:

مثال 7

حد را پیدا کنید

توجه! این نوع محدودیت بسیار رایج است، لطفاً این مثال را با دقت مطالعه کنید.

ما سعی می کنیم یک عدد بی نهایت بزرگ را در عبارت زیر علامت حد جایگزین کنیم:

نتیجه یک عدم قطعیت است. اما محدودیت قابل توجه دوم در مورد عدم قطعیت فرم اعمال می شود. چه باید کرد؟ شما باید پایه مدرک را تبدیل کنید. ما اینگونه استدلال می کنیم: در مخرج که داریم، به این معنی که ما نیز باید در صورت سازماندهی کنیم.

چندین محدودیت شگفت انگیز وجود دارد، اما معروف ترین آنها محدودیت های شگفت انگیز اول و دوم است. نکته قابل توجه در مورد این محدودیت ها این است که آنها به طور گسترده مورد استفاده قرار می گیرند و می توان از آنها برای یافتن محدودیت های دیگری که در مشکلات متعدد با آن مواجه می شوند استفاده کرد. این همان کاری است که ما در بخش عملی این درس انجام خواهیم داد. برای حل مسائل با کاهش به حد قابل توجه اول یا دوم، نیازی به افشای عدم قطعیت های موجود در آنها نیست، زیرا مقادیر این حدود مدت هاست توسط ریاضیدانان بزرگ استنباط شده است.

اولین محدودیت قابل توجهحد نسبت سینوس یک کمان بی‌نهایت کوچک به همان قوس نامیده می‌شود که در اندازه رادیانی بیان می‌شود:

بیایید به حل مشکلات در اولین حد قابل توجه برویم. توجه: اگر یک تابع مثلثاتی زیر علامت حد باشد، این تقریباً یک علامت مطمئن است که این عبارت را می توان به اولین حد قابل توجه کاهش داد.

مثال 1حد را پیدا کنید.

راه حل. در عوض تعویض ایکسصفر منجر به عدم قطعیت می شود:

مخرج یک سینوس است، بنابراین، عبارت را می توان به اولین حد قابل توجه کاهش داد. بیایید تحول را شروع کنیم:

در مخرج - سینوس سه x و در صورتگر فقط یک x وجود دارد، به این معنی که شما باید سه x را در صورتگر بگیرید. برای چی؟ برای ارائه 3 ایکس = آو بیان را دریافت کنید.

و به تغییری از اولین حد قابل توجه می رسیم:

چون مهم نیست در این فرمول چه حرفی (متغیر) به جای x باشد.

x را در سه ضرب می کنیم و بلافاصله تقسیم می کنیم:

مطابق با اولین حد قابل توجه ذکر شده، عبارت کسری را جایگزین می کنیم:

حالا بالاخره می توانیم این حد را حل کنیم:

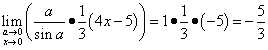مثال 2حد را پیدا کنید.

راه حل. جایگزینی مستقیم دوباره منجر به عدم قطعیت "صفر تقسیم بر صفر" می شود:

برای به دست آوردن اولین حد قابل توجه، لازم است که x زیر علامت سینوس در صورت و فقط x در مخرج با ضریب یکسان باشد. اجازه دهید این ضریب برابر با 2 باشد. برای انجام این کار، ضریب فعلی را در x به شکل زیر تصور کنید، با انجام اعمال با کسری، دریافت می کنیم:

مثال 3حد را پیدا کنید.

راه حل. هنگام جایگزینی، دوباره عدم قطعیت "صفر تقسیم بر صفر" را دریافت می کنیم:

احتمالاً قبلاً متوجه شده اید که از عبارت اصلی می توانید اولین حد شگفت انگیز ضرب در اولین حد شگفت انگیز را بدست آورید. برای این کار مربع های x در صورت و سینوس در مخرج را به ضرایب یکسان تجزیه می کنیم و برای اینکه ضرایب یکسانی برای x و سینوس بدست آوریم x را در صورت بر 3 تقسیم می کنیم و بلافاصله در 3 ضرب می کنیم.

مثال 4حد را پیدا کنید.

راه حل. باز هم عدم قطعیت "صفر تقسیم بر صفر" را دریافت می کنیم:

ما می توانیم نسبت دو حد قابل توجه اول را بدست آوریم. هم صورت و هم مخرج را بر x تقسیم می کنیم. سپس برای اینکه ضرایب در سینوس و x بر هم منطبق شوند، x بالایی را در 2 ضرب می کنیم و بلافاصله بر 2 تقسیم می کنیم و x پایین را در 3 ضرب می کنیم و بلافاصله بر 3 تقسیم می کنیم.

مثال 5حد را پیدا کنید.

راه حل. و باز هم عدم قطعیت "صفر تقسیم بر صفر":

از مثلثات به یاد داریم که مماس نسبت سینوس به کسینوس است و کسینوس صفر برابر با یک است. ما تغییراتی ایجاد می کنیم و به دست می آوریم:

مثال 6حد را پیدا کنید.

راه حل. تابع مثلثاتی در زیر علامت حد دوباره ایده اعمال اولین حد قابل توجه را پیشنهاد می کند. ما آن را به عنوان نسبت سینوس به کسینوس نشان می دهیم.

اولین حد قابل توجه برابری زیر نامیده می شود:

\begin(معادله)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(معادله)

از آنجایی که برای $\alpha\to(0)$ $\sin\alpha\to(0)$ داریم، می گوییم که اولین حد قابل توجه یک نامعین بودن شکل $\frac(0)(0)$ را نشان می دهد. به طور کلی، در فرمول (1)، به جای متغیر $\alpha$، در زیر علامت سینوس و در مخرج، هر عبارتی را می توان قرار داد، تا زمانی که دو شرط وجود داشته باشد:

عبارات زیر علامت سینوس و مخرج به طور همزمان به صفر تمایل دارند، یعنی. عدم قطعیت شکل $\frac(0)(0)$ وجود دارد.
عبارات زیر علامت سینوس و مخرج یکسان است.

نتایج حاصل از اولین حد قابل توجه نیز اغلب استفاده می شود:

\begin(معادله) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(معادله) \begin(معادله) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(معادله) \begin(معادله) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \پایان (معادله)

یازده مثال در این صفحه حل شده است. مثال شماره 1 به اثبات فرمول های (2)-(4) اختصاص دارد. مثال های #2، #3، #4 و #5 حاوی راه حل هایی با نظرات دقیق هستند. مثال‌های 6-10 حاوی راه‌حل‌هایی هستند که نظر کمی دارند یا بدون اظهار نظر هستند، همانطور که توضیحات مفصل در مثال‌های قبلی ارائه شد. هنگام حل، از برخی فرمول های مثلثاتی استفاده می شود که می توان آنها را یافت.

توجه داشته باشم که وجود توابع مثلثاتی، همراه با عدم قطعیت $\frac (0) (0)$، به این معنی نیست که اولین حد قابل توجه باید اعمال شود. گاهی اوقات تبدیل های مثلثاتی ساده کافی است - برای مثال، ببینید.

مثال شماره 1

ثابت کنید $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

الف) از آنجایی که $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$، پس:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\راست| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

از آنجایی که $\lim_(\alpha\to(0))\cos(0)=1$ و $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$، سپس:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

ب) بیایید جایگزین $\alpha=\sin(y)$ را بسازیم. از آنجایی که $\sin(0)=0$، پس از شرط $\alpha\to(0)$، $y\to(0)$ داریم. علاوه بر این، یک همسایگی صفر وجود دارد که $\arcsin\alpha=\arcsin(\sin(y))=y$، بنابراین:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\راست| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

برابری $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ ثابت شده است.

ج) جایگزین $\alpha=\tg(y)$ را بسازیم. از آنجایی که $\tg(0)=0$، شرایط $\alpha\to(0)$ و $y\to(0)$ معادل هستند. علاوه بر این، یک همسایگی صفر وجود دارد که در آن $\arctg\alpha=\arctg\tg(y))=y$ وجود دارد، بنابراین با تکیه بر نتایج نقطه a، خواهیم داشت:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\راست| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

برابری $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ ثابت شده است.

برابری های a)، b)، c) اغلب همراه با اولین حد قابل توجه استفاده می شود.

مثال شماره 2

حد محاسبه $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.

از آنجایی که $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ و $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$، یعنی. و صورت و مخرج کسر به طور همزمان به سمت صفر میل می کنند، پس در اینجا با عدم قطعیتی از شکل $\frac(0)(0)$، یعنی. انجام. علاوه بر این، مشاهده می شود که عبارات زیر علامت سینوس و مخرج یکسان است (یعنی و راضی است):

بنابراین، هر دو شرط ذکر شده در ابتدای صفحه وجود دارد. از این نتیجه می شود که فرمول قابل اجرا است، یعنی. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 )) = 1 دلار.

پاسخ: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\راست))(\frac(x^2-4)(x +7)) = 1 دلار.

مثال شماره 3

$\lim_(x\to(0))\frac(\sin(9x))(x)$ را پیدا کنید.

از آنجایی که $\lim_(x\to(0))\sin(9x)=0$ و $\lim_(x\to(0))x=0$، با عدم قطعیت شکل $\frac( سر و کار داریم 0 )(0)$، یعنی، انجام. با این حال، عبارات زیر علامت سینوس و در مخرج مطابقت ندارند. در اینجا لازم است عبارت در مخرج را به شکل دلخواه تنظیم کنید. ما نیاز داریم که عبارت $9x$ در مخرج باشد - سپس درست می شود. اساساً فاکتور $9$ را در مخرج از دست می دهیم که وارد کردن آن چندان سخت نیست، فقط عبارت موجود در مخرج را در $9$ ضرب کنید. به طور طبیعی، برای جبران ضرب در 9 دلار، باید بلافاصله بر 9 دلار تقسیم کنید و تقسیم کنید:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\راست| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x)) (9x) $$

حال عبارات مخرج و زیر علامت سینوس یکسان است. هر دو شرط برای محدودیت $\lim_(x\to(0))\frac(\sin(9x))(9x)$ برآورده می شود. بنابراین $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. و این بدان معنی است که:

$9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

پاسخ: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

مثال شماره 4

$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$ را پیدا کنید.

از آنجایی که $\lim_(x\to(0))\sin(5x)=0$ و $\lim_(x\to(0))\tg(8x)=0$، در اینجا با نامعین بودن $\frac(0)(0)$ را تشکیل دهید. با این حال، شکل اولین حد قابل توجه شکسته شده است. یک عدد شامل $\sin(5x)$ به $5x$ در مخرج نیاز دارد. در این شرایط، ساده‌ترین راه این است که صورت‌گر را بر 5x$ تقسیم کرده و بلافاصله در 5x$ ضرب کنیم. علاوه بر این، عملیات مشابهی را با مخرج انجام خواهیم داد و $\tg(8x)$ را در $8x$ ضرب و تقسیم می کنیم:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\چپ|\frac(0)(0)\راست| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

با کاهش $x$ و خارج کردن ثابت $\frac(5)(8)$ از علامت حد، دریافت می کنیم:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

توجه داشته باشید که $\lim_(x\to(0))\frac(\sin(5x))(5x)$ به طور کامل الزامات اولین حد قابل توجه را برآورده می کند. برای پیدا کردن $\lim_(x\to(0))\frac(\tg(8x))(8x)$ فرمول زیر قابل استفاده است:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$

پاسخ: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.

مثال شماره 5

$\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$ را پیدا کنید.

از آنجایی که $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (به یاد بیاورید که $\cos(0)=1$) و $\ lim_(x\to(0))x^2=0$، پس با نامعین بودن شکل $\frac(0)(0)$ روبرو هستیم. با این حال، برای اعمال اولین حد شگفت‌انگیز، باید با رفتن به سینوس (به منظور اعمال فرمول) یا مماس (برای اعمال فرمول) از کسینوس موجود در صورت خلاص شوید. شما می توانید این کار را با تبدیل زیر انجام دهید:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\راست)$$$$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$

بیایید به حد مجاز برگردیم:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\راست| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\راست) $$

کسر $\frac(\sin^2(5x))(x^2)$ در حال حاضر به شکل مورد نیاز برای اولین حد قابل توجه نزدیک است. بیایید کمی با کسری $\frac(\sin^2(5x))(x^2)$ کار کنیم و آن را به اولین حد شگفت‌انگیز تنظیم کنیم (توجه داشته باشید که عبارات در عدد و زیر سینوس باید مطابقت داشته باشند):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\راست)^2$$

بیایید به حد در نظر گرفته شده برگردیم:

$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\راست)^2 =25\cdot(1)\cdot( 1^2) = 25. $$

پاسخ: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

مثال شماره 6

حد $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$ را پیدا کنید.

از آنجایی که $\lim_(x\to(0))(1-\cos(6x))=0$ و $\lim_(x\to(0))(1-\cos(2x))=0$، پس ما با عدم قطعیت $\frac(0)(0)$ روبرو هستیم. بیایید با کمک اولین حد قابل توجه آن را باز کنیم. برای انجام این کار، اجازه دهید از کسینوس به سینوس حرکت کنیم. از آنجایی که $1-\cos(2\alpha)=2\sin^2(\alpha)$، پس:

$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

تبدیل شدن به محدودیت داده شدهبه سینوس ها خواهیم داشت:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\چپ|\frac(0)(0)\راست| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\راست)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$

پاسخ: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

مثال شماره 7

محاسبه حد $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ با توجه به $\alpha\neq\ beta $.

توضیحات مفصلی قبلا داده شد، اما در اینجا به سادگی توجه می کنیم که باز هم عدم تعینی $\frac(0)(0)$ وجود دارد. بیایید با استفاده از فرمول از کسینوس به سینوس حرکت کنیم

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

با استفاده از فرمول فوق به دست می آوریم:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\راست| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ بتا(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to (0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$

پاسخ: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ آلفا^2)(2)$.

مثال شماره 8

حد $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$ را پیدا کنید.

از آنجایی که $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (به یاد بیاورید که $\sin(0)=\tg(0)=0$) و $\ lim_(x\to(0))x^3=0$، پس در اینجا با نامعین بودن شکل $\frac(0)(0)$ سروکار داریم. بیایید آن را اینطور تجزیه کنیم:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\راست| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\راست))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\راست))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$

پاسخ: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.

مثال شماره 9

حد $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2)) را پیدا کنید.

از آنجایی که $\lim_(x\to(3))(1-\cos(x-3))=0$ و $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$، سپس نامشخصی به شکل $\frac(0)(0)$ وجود دارد. قبل از ادامه گسترش آن، راحت است که متغیر را طوری تغییر دهید که متغیر جدید به صفر برسد (توجه داشته باشید که متغیر $\alpha \ به 0$ در فرمول ها). ساده ترین راه معرفی متغیر $t=x-3$ است. با این حال، برای راحتی تغییرات بیشتر (این مزیت را می توان در مسیر راه حل زیر مشاهده کرد)، ارزش جایگزینی زیر را دارد: $t=\frac(x-3)(2)$. توجه داشته باشم که هر دو تعویض در این مورد قابل اجرا هستند، فقط تعویض دوم به شما امکان می دهد کمتر با کسری کار کنید. از $x\to(3)$، سپس $t\to(0)$.

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\چپ|\frac (0)(0)\right| =\چپ|\begin(تراز شده)&t=\frac(x-3)(2);\\&t\to(0)\end(تراز شده)\راست| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\راست) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

پاسخ: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.

مثال شماره 10

حد $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right) را پیدا کنید. 2) دلار.

باز هم با عدم قطعیت $\frac(0)(0)$ سروکار داریم. قبل از ادامه بسط آن، راحت است که یک تغییر متغیر را طوری ایجاد کنید که متغیر جدید به سمت صفر گرایش پیدا کند (توجه داشته باشید که در فرمول ها متغیر $\alpha\to(0)$ است). ساده ترین راه معرفی متغیر $t=\frac(\pi)(2)-x$ است. از $x\to\frac(\pi)(2)$، سپس $t\to(0)$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\راست)^2) =\left|\frac(0)(0)\right| =\چپ|\begin(تراز شده)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(تراز شده)\راست| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\راست)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$

پاسخ: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.

مثال شماره 11

یافتن محدودیت $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

در این صورت مجبور نیستیم از اولین حد فوق العاده استفاده کنیم. لطفا توجه داشته باشید: در هر دو حد اول و دوم، فقط توابع و اعداد مثلثاتی وجود دارد. اغلب، در نمونه هایی از این نوع، می توان عبارت واقع در زیر علامت حد را ساده کرد. در این صورت پس از ساده سازی مذکور و کاهش برخی عوامل، عدم قطعیت از بین می رود. من این مثال را تنها با یک هدف ارائه کردم: نشان دادن اینکه وجود توابع مثلثاتی در زیر علامت حد لزوماً به معنای اعمال اولین حد قابل توجه نیست.

از آنجایی که $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (به یاد بیاورید که $\sin\frac(\pi)(2)=1$) و $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (به یاد بیاورید که $\cos\frac(\pi)(2)=0$)، سپس با عدم قطعیت سروکار داریم از شکل $\frac(0)(0)$. با این حال، این به هیچ وجه به این معنی نیست که ما باید از اولین محدودیت قابل توجه استفاده کنیم. برای آشکار کردن عدم قطعیت، توجه به این نکته کافی است که $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\راست| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$

در کتاب حل دمیدویچ (شماره 475) راه حل مشابهی وجود دارد. در مورد محدودیت دوم، مانند مثال های قبلی این بخش، عدم قطعیت به شکل $\frac(0)(0)$ داریم. چرا بوجود می آید؟ به این دلیل به وجود می آید که $\tg\frac(2\pi)(3)=-\sqrt(3)$ و $2\cos\frac(2\pi)(3)=-1$. ما از این مقادیر برای تبدیل عبارات در صورت و مخرج استفاده می کنیم. هدف از اقدامات ما: جمع را در صورت و مخرج به عنوان حاصلضرب بنویسید. به هر حال، اغلب راحت است که یک متغیر را در یک فرم مشابه تغییر دهید تا متغیر جدید به سمت صفر گرایش پیدا کند (برای مثال به مثال های شماره 9 یا 10 در این صفحه مراجعه کنید). با این حال، در این مثال، جایگزین کردن متغیر هیچ فایده ای ندارد، اگرچه در صورت تمایل می توان جایگزینی متغیر $t=x-\frac(2\pi)(3)$ را آسان کرد.

$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\راست )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\راست))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\راست))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\راست)) =-\frac(4 )(\sqrt(3)). $$

همانطور که می بینید، ما مجبور نبودیم اولین محدودیت فوق العاده را اعمال کنیم. البته در صورت تمایل می توان این کار را انجام داد (به یادداشت زیر مراجعه کنید) اما ضروری نیست.

راه حل با استفاده از اولین حد قابل توجه چه خواهد بود؟ نمایش/پنهان کردن

با استفاده از اولین حد قابل توجه، دریافت می کنیم:

$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\راست))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ راست))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\راست) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$

پاسخ: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3)\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3)) دلار.