समीकरणों की एक प्रणाली को हल करने के लिए चित्रमय विधि। खुला पाठ "समीकरण प्रणालियों को हल करने के लिए ग्राफिक विधि

से अधिक विश्वसनीय ग्राफिक विधि, जिसकी चर्चा पिछले पैराग्राफ में की गई थी।

प्रतिस्थापन विधि

हमने इस पद्धति का उपयोग 7 वीं कक्षा में सिस्टम को हल करने के लिए किया था रेखीय समीकरण. 7 वीं कक्षा में विकसित किया गया एल्गोरिथ्म दो चर x और y के साथ किन्हीं दो समीकरणों (जरूरी नहीं कि रैखिक हो) की प्रणालियों को हल करने के लिए काफी उपयुक्त है (बेशक, चर को अन्य अक्षरों द्वारा निरूपित किया जा सकता है, जो कोई फर्क नहीं पड़ता)। वास्तव में, हमने पिछले भाग में इस एल्गोरिथम का उपयोग किया था, जब की समस्या दोहरा अंकनेतृत्व करने के लिए गणित का मॉडल, जो समीकरणों की एक प्रणाली है। हमने उपरोक्त समीकरणों की इस प्रणाली को प्रतिस्थापन विधि द्वारा हल किया है (उदाहरण 1 से 4 देखें)।

दो चर x, y के साथ दो समीकरणों की प्रणाली को हल करते समय प्रतिस्थापन विधि का उपयोग करने के लिए एल्गोरिदम।

1. निकाय के एक समीकरण से y को x के पदों में व्यक्त कीजिए।
2. निकाय के किसी अन्य समीकरण में y के स्थान पर परिणामी व्यंजक को रखिए।
3. x के परिणामी समीकरण को हल कीजिए।
4. पहले चरण में प्राप्त व्यंजक y से x में x के स्थान पर तीसरे चरण में प्राप्त समीकरण के प्रत्येक मूल को बारी-बारी से रखें।
5. उत्तर को मानों के जोड़े (x; y) के रूप में लिखें, जो क्रमशः तीसरे और चौथे चरण में पाए गए।

4) y के प्रत्येक पाए गए मान को सूत्र x \u003d 5 - Zy में बदलें। तो अगर
5) समीकरणों की दी गई प्रणाली के जोड़े (2; 1) और समाधान।

उत्तर: (2; 1);

बीजीय जोड़ विधि

यह विधि, प्रतिस्थापन विधि की तरह, 7वीं कक्षा के बीजगणित पाठ्यक्रम से परिचित है, जहाँ इसका उपयोग रैखिक समीकरणों की प्रणालियों को हल करने के लिए किया गया था। हम निम्नलिखित उदाहरण में विधि के सार को याद करते हैं।

उदाहरण 2समीकरणों की एक प्रणाली को हल करें

हम सिस्टम के पहले समीकरण के सभी पदों को 3 से गुणा करते हैं, और दूसरे समीकरण को अपरिवर्तित छोड़ देते हैं:
सिस्टम के दूसरे समीकरण को उसके पहले समीकरण से घटाएं:

मूल प्रणाली के दो समीकरणों के बीजगणितीय जोड़ के परिणामस्वरूप, एक समीकरण प्राप्त हुआ जो दिए गए सिस्टम के पहले और दूसरे समीकरणों की तुलना में सरल है। इस सरल समीकरण के साथ, हमें किसी दिए गए सिस्टम के किसी भी समीकरण को बदलने का अधिकार है, उदाहरण के लिए, दूसरा। तब समीकरणों की दी गई प्रणाली को एक सरल प्रणाली द्वारा प्रतिस्थापित किया जाएगा:

इस प्रणाली को प्रतिस्थापन विधि द्वारा हल किया जा सकता है। दूसरे समीकरण से हम पाते हैं कि इस व्यंजक को y के स्थान पर निकाय के पहले समीकरण में प्रतिस्थापित करने पर, हम प्राप्त करते हैं

यह x के पाए गए मानों को सूत्र में बदलने के लिए बनी हुई है

अगर एक्स = 2 तो

इस प्रकार, हमने सिस्टम के दो समाधान खोजे हैं:

नए चर पेश करने की विधि

आप 8वीं कक्षा के बीजगणित पाठ्यक्रम में एक चर के साथ परिमेय समीकरणों को हल करते समय एक नए चर को प्रस्तुत करने की विधि से परिचित हो गए। समीकरणों की प्रणालियों को हल करने के लिए इस पद्धति का सार समान है, लेकिन तकनीकी दृष्टिकोण से कुछ विशेषताएं हैं जिनकी चर्चा हम निम्नलिखित उदाहरणों में करेंगे।

उदाहरण 3समीकरणों की एक प्रणाली को हल करें

आइए एक नए चर का परिचय दें फिर सिस्टम के पहले समीकरण को और अधिक में फिर से लिखा जा सकता है अराल तरीका: आइए इस समीकरण को चर t के लिए हल करें:

ये दोनों मान स्थिति को संतुष्ट करते हैं, और इसलिए मूल हैं तर्कसंगत समीकरणपरिवर्तनीय टी के साथ लेकिन इसका मतलब है कि या तो जहां से हम पाते हैं कि x = 2y, या
इस प्रकार, एक नए चर को पेश करने की विधि की मदद से, हम सिस्टम के पहले समीकरण को "स्तरीकृत" करने में सक्षम थे, जो दिखने में काफी जटिल है, दो सरल समीकरणों में:

एक्स = 2 वाई; वाई - 2x।

आगे क्या होगा? और फिर दोनों में से प्रत्येक ने प्राप्त किया सरल समीकरणसिस्टम में बदले में समीकरण x 2 - y 2 \u003d 3 के साथ विचार करना आवश्यक है, जिसे हमने अभी तक याद नहीं किया है। दूसरे शब्दों में, समीकरणों की दो प्रणालियों को हल करने में समस्या कम हो जाती है:

पहली प्रणाली, दूसरी प्रणाली के लिए समाधान खोजना और उत्तर में सभी परिणामी मूल्यों के जोड़े शामिल करना आवश्यक है। आइए समीकरणों की पहली प्रणाली को हल करें:

आइए प्रतिस्थापन विधि का उपयोग करें, खासकर जब से यहां इसके लिए सब कुछ तैयार है: हम सिस्टम के दूसरे समीकरण में एक्स के बजाय एक्सप्रेशन 2y को प्रतिस्थापित करते हैं। प्राप्त

चूंकि x \u003d 2y, हम क्रमशः x 1 \u003d 2, x 2 \u003d 2 पाते हैं। इस प्रकार, दिए गए सिस्टम के दो समाधान प्राप्त होते हैं: (2; 1) और (-2; -1)। आइए समीकरणों की दूसरी प्रणाली को हल करें:

आइए प्रतिस्थापन विधि का फिर से उपयोग करें: हम सिस्टम के दूसरे समीकरण में y के बजाय अभिव्यक्ति 2x को प्रतिस्थापित करते हैं। प्राप्त

इस समीकरण की कोई जड़ नहीं है, जिसका अर्थ है कि समीकरण प्रणाली का कोई हल नहीं है। इस प्रकार, उत्तर में केवल पहली प्रणाली के समाधान शामिल किए जाने चाहिए।

उत्तर: (2; 1); (-2; -1)।

दो चर वाले दो समीकरणों के सिस्टम को हल करने में नए चरों को पेश करने की विधि का उपयोग दो संस्करणों में किया जाता है। पहला विकल्प: सिस्टम के केवल एक समीकरण में एक नया चर पेश किया जाता है और उसका उपयोग किया जाता है। उदाहरण 3 में ठीक ऐसा ही हुआ। दूसरा विकल्प: सिस्टम के दोनों समीकरणों में एक साथ दो नए चर पेश किए जाते हैं और उनका उपयोग किया जाता है। उदाहरण 4 में ऐसा ही होगा।

उदाहरण 4समीकरणों की एक प्रणाली को हल करें

आइए दो नए चर पेश करें:

हम सीखते हैं कि तब

यह आपको फिर से लिखने की अनुमति देगा दी गई प्रणालीबहुत सरल रूप में, लेकिन नए चर a और b के संबंध में:

a \u003d 1 के बाद से, समीकरण a + 6 \u003d 2 से हम पाते हैं: 1 + 6 \u003d 2; 6=1. इस प्रकार, चर a और b के लिए, हमें एक हल मिला:

चर x और y पर लौटने पर, हम समीकरणों की प्रणाली प्राप्त करते हैं

इस प्रणाली को हल करने के लिए, हम विधि लागू करते हैं बीजीय जोड़:

तब से समीकरण 2x + y = 3 से हम पाते हैं:
इस प्रकार, चर x और y के लिए, हमें एक हल मिला:

आइए इस खंड को एक संक्षिप्त लेकिन गंभीर सैद्धांतिक चर्चा के साथ समाप्त करें। क्या आपने पहले ही हल करने में कुछ अनुभव प्राप्त कर लिया है विभिन्न समीकरण: रैखिक, वर्ग, परिमेय, अपरिमेय। आप जानते हैं कि एक समीकरण को हल करने का मुख्य विचार यह है कि एक समीकरण से दूसरे में धीरे-धीरे जाना, सरल लेकिन दिए गए समीकरण के बराबर। पिछले भाग में, हमने दो चरों वाले समीकरणों के लिए तुल्यता की धारणा का परिचय दिया था। इस अवधारणा का उपयोग समीकरणों की प्रणालियों के लिए भी किया जाता है।

परिभाषा।

चर x और y वाले समीकरणों की दो प्रणालियों को समतुल्य कहा जाता है यदि उनके समान समाधान हैं या यदि दोनों प्रणालियों का कोई समाधान नहीं है।

इस खंड में हमने जिन तीनों विधियों (प्रतिस्थापन, बीजगणितीय जोड़ और नए चरों का परिचय) की चर्चा की है, वे तुल्यता की दृष्टि से बिल्कुल सही हैं। दूसरे शब्दों में, इन विधियों का उपयोग करते हुए, हम समीकरणों की एक प्रणाली को दूसरे, सरल, लेकिन मूल प्रणाली के समतुल्य से बदल देते हैं।

समीकरणों की प्रणालियों को हल करने के लिए चित्रमय विधि

हम पहले ही सीख चुके हैं कि प्रतिस्थापन की विधि, बीजीय योग और नए चरों के परिचय जैसे सामान्य और विश्वसनीय तरीकों से समीकरणों की प्रणालियों को कैसे हल किया जाए। और अब आइए उस विधि को याद करें जिसका अध्ययन आप पिछले पाठ में कर चुके हैं। अर्थात्, आलेखीय समाधान पद्धति के बारे में आप जो जानते हैं उसे दोहराते हैं।

समीकरणों की प्रणालियों को ग्राफिक रूप से हल करने की विधि प्रत्येक विशिष्ट समीकरणों के लिए एक ग्राफ का निर्माण है जो इस प्रणाली में शामिल हैं और एक में हैं कार्तिकये निर्देशांक, और यह भी कि जहां इन ग्राफों के बिंदुओं के प्रतिच्छेदन को खोजना आवश्यक है। समीकरणों की इस प्रणाली को हल करने के लिए इस बिंदु (x; y) के निर्देशांक हैं।

यह याद रखना चाहिए कि ग्राफिक्स सिस्टमसमीकरणों में या तो एक अद्वितीय होता है सही निर्णय, या अनंत संख्या में समाधान, या कोई समाधान नहीं है।

आइए अब इनमें से प्रत्येक समाधान पर करीब से नज़र डालें। और इसलिए, समीकरणों की प्रणाली हो सकती है केवल निर्णययदि रेखाएँ, जो निकाय के समीकरणों के आलेख हैं, प्रतिच्छेद करती हैं। यदि ये रेखाएँ समानांतर हैं, तो समीकरणों की ऐसी प्रणाली का कोई हल नहीं है। प्रणाली के समीकरणों के प्रत्यक्ष रेखांकन के संयोग के मामले में, ऐसी प्रणाली आपको कई समाधान खोजने की अनुमति देती है।

खैर, अब आइए एक ग्राफिकल विधि का उपयोग करके 2 अज्ञात के साथ दो समीकरणों की प्रणाली को हल करने के लिए एल्गोरिदम पर एक नज़र डालें:

सबसे पहले, हम पहले समीकरण का एक ग्राफ बनाते हैं;
दूसरा चरण दूसरे समीकरण से संबंधित एक ग्राफ तैयार करना होगा;
तीसरा, हमें रेखांकन के प्रतिच्छेदन बिंदुओं को खोजने की आवश्यकता है।
और परिणामस्वरूप, हमें प्रत्येक प्रतिच्छेदन बिंदु के निर्देशांक मिलते हैं, जो समीकरणों की प्रणाली का समाधान होगा।

आइए इस विधि को एक उदाहरण के साथ और अधिक विस्तार से देखें। हमें हल करने के लिए समीकरणों की एक प्रणाली दी गई है:

समीकरण हल करना

1. सबसे पहले, हम इस समीकरण का एक ग्राफ बनाएंगे: x2+y2=9।

लेकिन यह ध्यान दिया जाना चाहिए कि समीकरणों का यह ग्राफ मूल बिंदु पर केंद्रित एक वृत्त होगा, और इसकी त्रिज्या तीन के बराबर होगी।

2. हमारा अगला कदम एक समीकरण तैयार करना होगा जैसे: y = x - 3।

इस मामले में, हमें एक रेखा बनानी होगी और अंक (0;−3) और (3;0) खोजने होंगे।

3. आइए देखें कि हमें क्या मिला। हम देखते हैं कि रेखा वृत्त को उसके दो बिंदुओं A और B पर काटती है।

अब हम इन बिंदुओं के निर्देशांक ढूंढ रहे हैं। हम देखते हैं कि निर्देशांक (3;0) बिंदु A के अनुरूप हैं, और निर्देशांक (0;-3) बिंदु B के अनुरूप हैं।

और इसके परिणामस्वरूप हमें क्या मिलता है?

एक वृत्त के साथ एक सीधी रेखा के प्रतिच्छेदन पर प्राप्त संख्याएँ (3;0) और (0;−3) प्रणाली के दोनों समीकरणों के सटीक समाधान हैं। और इससे यह निष्कर्ष निकलता है कि ये संख्याएँ भी इस समीकरण प्रणाली के हल हैं।

अर्थात्, इस समाधान का उत्तर संख्याएँ हैं: (3;0) और (0;−3)।

इस पाठ में, हम दो चरों वाले दो समीकरणों के निकाय को हल करने पर विचार करेंगे। सबसे पहले, दो रैखिक समीकरणों की एक प्रणाली के ग्राफिकल समाधान पर विचार करें, उनके ग्राफ की समग्रता की विशिष्टताएं। इसके बाद, हम ग्राफिकल विधि का उपयोग करके कई प्रणालियों को हल करते हैं।

विषय: समीकरणों की प्रणाली

पाठ: समीकरणों के निकाय को हल करने की आलेखीय विधि

प्रणाली पर विचार करें

संख्याओं की एक जोड़ी जो एक साथ सिस्टम के पहले और दूसरे दोनों समीकरणों का समाधान है, कहलाती है समीकरणों की प्रणाली का समाधान.

समीकरणों की एक प्रणाली को हल करने का अर्थ है इसके सभी समाधान खोजना, या यह स्थापित करना कि कोई समाधान नहीं हैं। हमने बुनियादी समीकरणों के रेखांकन पर विचार किया है, आइए प्रणालियों के विचार पर आगे बढ़ते हैं।

उदाहरण 1. सिस्टम को हल करें

समाधान:

ये रैखिक समीकरण हैं, इनमें से प्रत्येक का आलेख एक सीधी रेखा है। पहले समीकरण का ग्राफ बिंदुओं (0; 1) और (-1; 0) से होकर गुजरता है। दूसरे समीकरण का ग्राफ बिंदुओं (0; -1) और (-1; 0) से होकर गुजरता है। रेखाएँ बिंदु (-1; 0) पर प्रतिच्छेद करती हैं, यह समीकरणों के निकाय का हल है ( चावल। 1).

प्रणाली का हल संख्याओं का एक युग्म है। संख्याओं के इस युग्म को प्रत्येक समीकरण में प्रतिस्थापित करने पर, हम सही समानता प्राप्त करते हैं।

हमने रैखिक प्रणाली का एकमात्र समाधान प्राप्त किया है।

याद रखें कि एक रैखिक प्रणाली को हल करते समय, निम्नलिखित मामले संभव हैं:

प्रणाली का एक अनूठा समाधान है - रेखाएं प्रतिच्छेद करती हैं,

प्रणाली का कोई समाधान नहीं है - रेखाएं समानांतर हैं,

सिस्टम में अनंत संख्या में समाधान हैं - रेखाएं मेल खाती हैं।

हमने निकाय की एक विशेष स्थिति पर विचार किया है, जब p(x; y) और q(x; y) x और y के रैखिक व्यंजक हैं।

उदाहरण 2. समीकरणों के निकाय को हल करें

समाधान:

पहले समीकरण का आलेख एक सीधी रेखा है, दूसरे समीकरण का आलेख एक वृत्त है। आइए बिंदुओं द्वारा पहला ग्राफ बनाएं (चित्र 2)।

वृत्त का केंद्र बिंदु O(0; 0) पर है, त्रिज्या 1 है।

ग्राफ़ बिंदु A(0; 1) और बिंदु B(-1; 0) पर प्रतिच्छेद करते हैं।

उदाहरण 3. सिस्टम को ग्राफिक रूप से हल करें

हल: आइए पहले समीकरण का एक ग्राफ बनाएं - यह एक वृत्त है जिसका केंद्र बिंदु O (0; 0) पर है और 2 की त्रिज्या है। दूसरे समीकरण का ग्राफ एक परवलय है। इसे मूल के सापेक्ष 2 ऊपर की ओर स्थानांतरित किया जाता है, अर्थात। इसका शीर्ष बिंदु (0; 2) (चित्र 3) है।

रेखांकन में एक है आम बात- टी। ए (0; 2)। यह व्यवस्था का समाधान है। शुद्धता की जाँच के लिए समीकरण में कुछ संख्याएँ रखें।

उदाहरण 4. सिस्टम को हल करें

हल: आइए पहले समीकरण का एक ग्राफ बनाते हैं - यह एक वृत्त है जिसका केंद्र O (0; 0) पर है और 1 की त्रिज्या है (चित्र 4)।

आइए फ़ंक्शन का एक ग्राफ बनाएं यह एक टूटी हुई रेखा है (चित्र 5)।

अब इसे oy अक्ष के अनुदिश 1 से नीचे ले जाएँ। यह फ़ंक्शन का ग्राफ होगा

आइए दोनों ग्राफों को एक ही निर्देशांक प्रणाली में रखें (चित्र 6)।

हमें तीन प्रतिच्छेदन बिंदु मिलते हैं - बिंदु A (1; 0), बिंदु B (-1; 0), बिंदु C (0; -1)।

हमने सिस्टम को हल करने के लिए एक ग्राफिकल विधि पर विचार किया है। यदि प्रत्येक समीकरण को रेखांकन करना और प्रतिच्छेदन बिंदुओं के निर्देशांक ज्ञात करना संभव है, तो यह विधि काफी पर्याप्त है।

लेकिन अक्सर ग्राफिकल विधि से सिस्टम का केवल एक अनुमानित समाधान खोजना संभव हो जाता है या समाधानों की संख्या के बारे में प्रश्न का उत्तर देना संभव हो जाता है। इसलिए, अन्य विधियों, अधिक सटीक, की आवश्यकता है, और हम अगले पाठों में उनके साथ व्यवहार करेंगे।

1. मोर्दकोविच ए.जी. और अन्य बीजगणित 9वीं कक्षा: प्रोक। सामान्य शिक्षा के लिए संस्थान - चौथा संस्करण। - एम .: मेनेमोसिन, 2002.-192 पी .: बीमार।

2. मोर्दकोविच ए.जी. एट अल। बीजगणित ग्रेड 9: शैक्षणिक संस्थानों के छात्रों के लिए कार्यपुस्तिका / ए जी मोर्दकोविच, टी। एन। मिशुस्टिना एट अल। - चौथा संस्करण। - एम .: मेमोसिन, 2002.-143 पी .: बीमार।

3. यू। एन। मकारिचेव, बीजगणित। ग्रेड 9: पाठ्यपुस्तक। सामान्य शिक्षा के छात्रों के लिए। संस्थान / यू। एन। मकारिचेव, एन। जी। मिंड्युक, के। आई। नेशकोव, आई। ई। फेओक्टिस्टोव। - 7 वां संस्करण।, रेव। और अतिरिक्त - एम।: निमोसिन, 2008।

4. अलीमोव श.ए., कोल्यागिन यू.एम., सिदोरोव यू.वी. बीजगणित। श्रेणी 9 16वां संस्करण। - एम।, 2011. - 287 पी।

5. मोर्दकोविच ए.जी. बीजगणित। श्रेणी 9 दोपहर 2 बजे भाग 1। शैक्षणिक संस्थानों के छात्रों के लिए पाठ्यपुस्तक / ए। जी। मोर्दकोविच, पी। वी। सेमेनोव। - 12 वां संस्करण।, मिटा दिया गया। — एम .: 2010। — 224 पी .: बीमार।

6. बीजगणित। श्रेणी 9 2 घंटे में। भाग 2। शैक्षिक संस्थानों के छात्रों के लिए टास्क बुक / ए। जी। मोर्दकोविच, एल। ए। अलेक्जेंड्रोवा, टी। एन। मिशुस्टिना और अन्य; ईडी। ए जी मोर्दकोविच। - 12 वां संस्करण।, रेव। - एम .: 2010.-223 पी .: बीमार।

1. College.ru गणित पर अनुभाग ()।

2. इंटरनेट परियोजना "कार्य" ()।

3. शैक्षिक पोर्टल"मैं उपयोग का समाधान करूंगा" ()।

1. मोर्दकोविच ए.जी. एट अल। बीजगणित ग्रेड 9: शैक्षणिक संस्थानों के छात्रों के लिए कार्यपुस्तिका / ए जी मोर्दकोविच, टी। एन। मिशुस्टिना एट अल। - चौथा संस्करण। - एम ।: मेनेमोसिन, 2002.-143 पी .: बीमार। नंबर 105, 107, 114, 115।

समीकरणों के सिस्टम को हल करने का ग्राफिकल तरीका

(9 वां दर्जा)

पाठ्यपुस्तक: बीजगणित, ग्रेड 9, तेल्याकोवस्की एस.ए. द्वारा संपादित।

पाठ का प्रकार: ज्ञान, कौशल, क्षमताओं के जटिल अनुप्रयोग में एक पाठ।

पाठ मकसद:

शैक्षिक:एक जटिल में स्वतंत्र रूप से ज्ञान को लागू करने की क्षमता विकसित करें, इसे नई स्थितियों में स्थानांतरित करें, जिसमें फ़ंक्शन ग्राफ़ प्लॉट करने के लिए कंप्यूटर प्रोग्राम के साथ काम करना और दिए गए समीकरणों में जड़ों की संख्या का पता लगाना शामिल है।

शिक्षात्मक: मुख्य विशेषताओं को उजागर करने, समानताएं और अंतर स्थापित करने के लिए छात्रों की क्षमता बनाने के लिए। समृद्ध शब्दावली. भाषण विकसित करें, इसे जटिल करें सिमेंटिक फंक्शन. विकास करना तार्किक सोच, संज्ञानात्मक रुचि, ग्राफिक निर्माण की संस्कृति, स्मृति, जिज्ञासा।

शिक्षात्मक: अपने काम के परिणाम के लिए जिम्मेदारी की भावना पैदा करें। सहपाठियों की सफलताओं और असफलताओं के साथ सहानुभूति रखना सीखें।

शिक्षा के साधन : कंप्यूटर, मल्टीमीडिया प्रोजेक्टर, हैंडआउट।

शिक्षण योजना:

आयोजन का समय. गृहकार्य - 2 मिनट।

बोध, पुनरावृत्ति, ज्ञान का सुधार - 8 मिनट।

नई सामग्री सीखना - 10 मि.

व्यावहारिक कार्य - 20 मिनट।

संक्षेप में - 4 मिनट।

प्रतिबिंब - 1 मिनट।

कक्षाओं के दौरान

संगठनात्मक क्षण - 2 मिनट।

हैलो दोस्तों! आज का पाठ महत्वपूर्ण विषय: "समीकरणों की प्रणालियों का समाधान"।

सटीक विज्ञान में ज्ञान के ऐसे कोई क्षेत्र नहीं हैं, जहां भी इस विषय को लागू किया जाता है। हमारे पाठ का एपिग्राफ है निम्नलिखित शब्द: "मन न केवल ज्ञान में है, बल्कि ज्ञान को व्यवहार में लागू करने की क्षमता में भी है" ". (अरस्तू)

पाठ के विषय, लक्ष्य और उद्देश्य निर्धारित करना।

शिक्षक कक्षा को इस बारे में सूचित करता है कि पाठ में क्या अध्ययन किया जाएगा और यह सीखने का कार्य निर्धारित करता है कि ग्राफिकल तरीके से दो चर वाले समीकरणों की प्रणाली को कैसे हल किया जाए।

होमवर्क (पी.18 नंबर 416, 418, 419 ए)।

सैद्धांतिक सामग्री की पुनरावृत्ति - 8 मिनट।

लेकिन) गणित शिक्षक: तैयार चित्रों के अनुसार, प्रश्नों के उत्तर दें और अपने उत्तर का औचित्य सिद्ध करें।

1). ग्राफ खोजें द्विघात फंक्शनडी = 0 (छात्र प्रश्न का उत्तर देते हैं और ग्राफ 3c नाम देते हैं)।

2). k > 0 . के व्युत्क्रमानुपाती फलन का आलेख ज्ञात कीजिए (छात्र प्रश्न का उत्तर देते हैं, ग्राफ़ 3 पर कॉल करेंएक ).

3). केंद्र O(-1; -5) वाले वृत्त का आलेख ज्ञात कीजिए। (छात्र प्रश्न का उत्तर देते हैं, ग्राफ़ 1b पर कॉल करें)।

4). फलन y =3x -2 का आलेख ज्ञात कीजिए। (छात्र प्रश्न का उत्तर देते हैं और ग्राफ 3बी नाम देते हैं)।

5). द्विघात फलन D >0, a >0 का आलेख ज्ञात कीजिए। (छात्र प्रश्न का उत्तर देते हैं और नाम ग्राफ 1एक ).

गणित शिक्षक: – समीकरणों के सिस्टम को सफलतापूर्वक हल करने के लिए, आइए याद रखें:

एक)। समीकरणों की एक प्रणाली क्या है? (समीकरणों की एक प्रणाली को कई समीकरण कहा जाता है जिसके लिए अज्ञात के मूल्यों को खोजने की आवश्यकता होती है जो इन सभी समीकरणों को एक साथ संतुष्ट करते हैं)।

2))। समीकरणों की एक प्रणाली को हल करने का क्या मतलब है? (समीकरणों की एक प्रणाली को हल करने का अर्थ है सभी समाधान खोजना या यह साबित करना कि कोई समाधान नहीं हैं)।

3))। समीकरणों की एक प्रणाली का समाधान क्या है? (समीकरणों की एक प्रणाली का समाधान संख्याओं की एक जोड़ी (x; y) है, जिसमें सिस्टम के सभी समीकरण वास्तविक समानता में बदल जाते हैं)।

4) ज्ञात कीजिए कि क्या समीकरणों के निकाय का हल है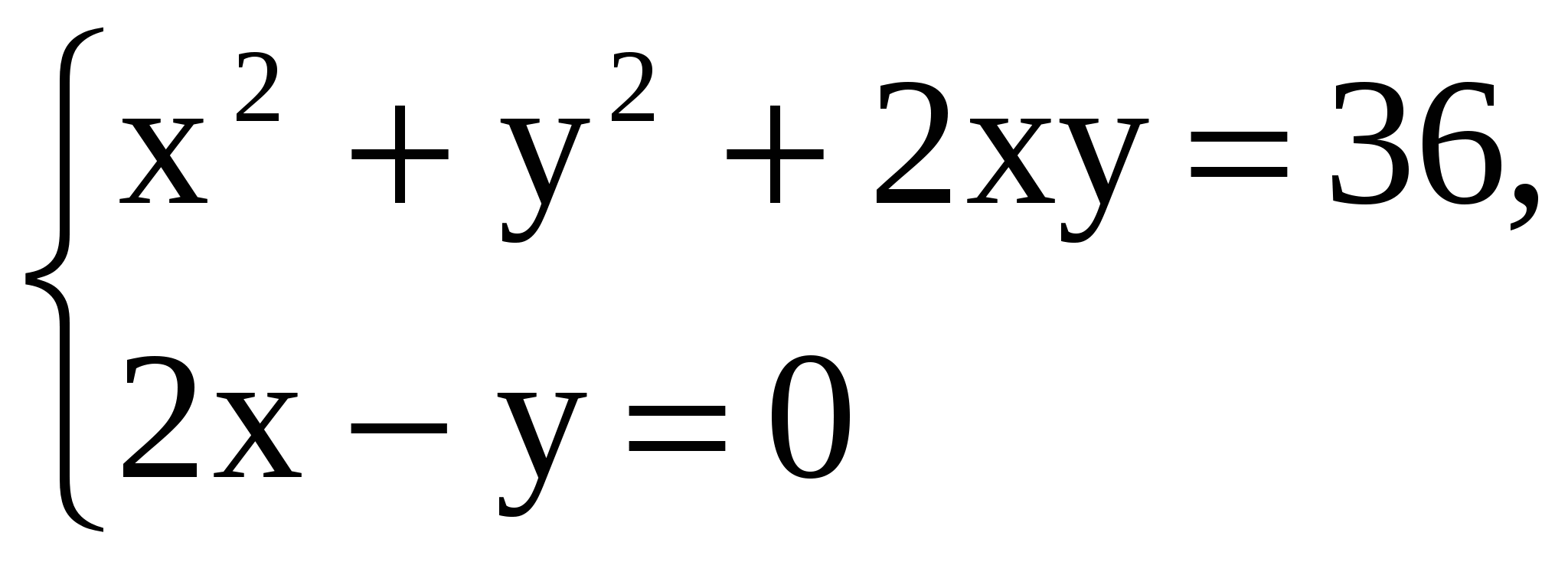
संख्याओं का युग्म: क) x = 1, y = 2;(–) बी) एक्स = 2, वाई = 4; (+) सी) एक्स \u003d - 2, वाई \u003d - 4? (+)

तृतीय नई सामग्री- दस मिनट।

पाठ्यपुस्तक का आइटम 18 बातचीत की विधि द्वारा प्रस्तुत किया गया है.

गणित शिक्षक: 7 वीं कक्षा के बीजगणित पाठ्यक्रम में, हमने पहली डिग्री के समीकरणों के सिस्टम पर विचार किया। अब आइए पहली और दूसरी डिग्री के समीकरणों से बने सिस्टम के समाधान से निपटें।

1. समीकरणों के निकाय को क्या कहते हैं?

2. समीकरणों के निकाय को हल करने का क्या अर्थ है?

हम जानते हैं कि बीजगणितीय विधि आपको सिस्टम के सटीक समाधान खोजने की अनुमति देती है, और ग्राफिकल विधि आपको यह देखने की अनुमति देती है कि सिस्टम की कितनी जड़ें हैं और उन्हें लगभग ढूंढा जा सकता है। इसलिए, हम सीखना जारी रखेंगे कि अगले पाठों में दूसरी डिग्री के समीकरणों के सिस्टम को कैसे हल किया जाए, और आज पाठ का मुख्य लक्ष्य होगा प्रायोगिक उपयोगफ़ंक्शन ग्राफ़ की साजिश रचने और समीकरणों की प्रणालियों की जड़ों की संख्या का पता लगाने के लिए एक कंप्यूटर प्रोग्राम।

चतुर्थ . व्यावहारिक कार्य - 20 मिनट। ग्राफिक रूप से समीकरणों की प्रणाली को हल करना। समीकरणों की जड़ों का निर्धारण।(कंप्यूटर पर ग्राफ प्लॉट करना।)

कंप्यूटर पर छात्रों द्वारा असाइनमेंट पूरे किए जाते हैं। ऑपरेशन के दौरान समाधान की जाँच की जाती है।

वाई=2x2+5x+3

वाई = 4

वाई \u003d -2x 2 + 5x + 3

वाई=-3x+4

वाई = -2x2 -5x-3

वाई=-4+2x

वाई=4x2+5x+3

वाई = 2

आप= -4 एक्स 2 +5x+3

वाई=-3x+2

वाई = -4x2 -5x-3

वाई=-2+2x

आप = 4 एक्स 2 + 5 एक्स+5

वाई = 3

वाई = -4x2 +5x+5

वाई=-एक्स+3

वाई = -4x2 -5x-5

वाई=-2+3x

यहाँ दो समीकरणों के रेखांकन हैं। इन समीकरणों द्वारा परिभाषित निकाय और उसके हल को लिखिए।

– निम्न में से कौन से प्रणालीक्या आप इस तस्वीर से हल कर सकते हैं?

– 4 प्रणालियाँ दी गई थीं, उन्हें रेखांकन के साथ सहसंबद्ध करना था। अब कार्य उलट गया है: वहाँ है चार्टउन्हें सिस्टम से जोड़ने की जरूरत है।

1. पाठ को सारांशित करना। ग्रेडिंग - 4 मिनट।

* समीकरणों की प्रणाली को हल करना। ( तारक के साथ कार्य*.)

छात्रों के पहले समूह के लिए समीकरण:

छात्रों के दूसरे समूह के लिए समीकरण:

छात्रों के तीसरे समूह के लिए समीकरण:

एक्स आप = 6

एक्स 2 + आप = 4

एक्स 2 + वाई = 3

एक्स - वाई + 1= 0

एक्स 2 - वाई = 3

तारीख: ________________

विषय: बीजगणित

विषय: "समीकरणों की प्रणाली को हल करने के लिए ग्राफिक विधि।"

लक्ष्य:समीकरणों के सिस्टम को हल करने के लिए ग्राफ़ का उपयोग करें।

कार्य:

शैक्षिक: दो चरों वाले रैखिक समीकरणों के निकाय को आलेखीय रूप से हल करना सिखाएं।

विकसित होना: छात्रों की अनुसंधान क्षमताओं का विकास, आत्म-नियंत्रण, भाषण।

पोषण: संचार, सटीकता की संस्कृति को बढ़ावा देना।

पाठ प्रकार:संयुक्त

प्रपत्र:ललाट सर्वेक्षण, जोड़े में काम करें।

कक्षाओं के दौरान:

संगठनात्मक चरण। पाठ के विषय की रिपोर्ट करना, पाठ के लक्ष्य निर्धारित करना।(एक नोटबुक में संख्या, विषय लिखें)

कवर की गई सामग्री की पुनरावृत्ति और समेकन:

1. इंतिहान गृहकार्य(अनसुलझी समस्याओं का विश्लेषण);

   सामग्री के आत्मसात का नियंत्रण:

बुनियादी ज्ञान का अद्यतनीकरण:

दो चरों में एक रैखिक समीकरण की परिभाषा।

दो चरों वाले रैखिक समीकरण के हल को क्या कहते हैं?

दो चरों वाले रैखिक समीकरण के ग्राफ को क्या कहते हैं?

दो चरों वाले रैखिक समीकरण का आलेख क्या होता है?

एक रेखा को कितने बिंदु परिभाषित करते हैं?

समीकरणों की एक प्रणाली को हल करने का क्या मतलब है?

दो चरों वाले रैखिक समीकरणों के निकाय का हल क्या कहलाता है?

समतल में दो रेखाएँ कब प्रतिच्छेद करती हैं?

समतल में दो रेखाएँ समानांतर कब होती हैं?

समतल में दो सीधी रेखाएँ कब मिलती हैं?

नई सामग्री सीखना:

विचार करना दो अज्ञात के साथ दो समीकरणों की प्रणाली. फेसलासमीकरणों के निकाय कहलाते हैं मूल्यों की जोड़ीचर, कौन मुड़ता है प्रणाली के प्रत्येक समीकरण को सही समानता में. समीकरणों की एक प्रणाली को हल करने का अर्थ है इसके सभी समाधान खोजना या यह साबित करना कि कोई समाधान नहीं है।

सबसे प्रभावी में से एक और दृश्य तरीकेसमीकरणों और समीकरणों की प्रणालियों को हल करना और शोध करना ग्राफिक तरीका।

दो चर के साथ एक समीकरण की साजिश रचने के लिए एल्गोरिदम।

चर y को x के पदों में व्यक्त कीजिए।

ग्राफ़ को परिभाषित करने वाले बिंदुओं को "ले"।

प्लॉट समीकरण

ग्राफिकल तरीके से दो चर वाले समीकरणों की एक प्रणाली को हल करने के लिए एल्गोरिदम।

निकाय के प्रत्येक समीकरण के आलेखों की रचना कीजिए।

प्रतिच्छेदन बिंदु के निर्देशांक ज्ञात कीजिए।

उत्तर लिखिए।

उदाहरण 1

आइए समीकरणों की प्रणाली को हल करें:

आइए हम एक समन्वय प्रणाली में पहले के ग्राफिक्स का निर्माण करें एक्स 2 + वाई 2 = 25
(सर्कल) और दूसरा हू= 12 (हाइपरबोला) समीकरण। यह स्पष्ट है कि
समीकरण रेखांकन चार बिंदुओं पर प्रतिच्छेद करते हैं लेकिन(3; 4), पर(4; 3)
सी(-3;-4) और डी(-4; 3), जिनके निर्देशांक हल हैं
एक प्रणाली।

टी
चूंकि समाधान एक निश्चित सटीकता के साथ एक ग्राफिकल विधि के साथ पाया जा सकता है, उन्हें प्रतिस्थापन द्वारा सत्यापित किया जाना चाहिए।

जाँच से पता चलता है कि सिस्टम के वास्तव में चार समाधान हैं: (3;4),(4;3),(-3;-4),(-4;-3)।

पाठ में कार्य:संख्या 415 (बी); संख्या 416; संख्या 419 (बी); नंबर 420 (बी); नंबर 421 (ए, बी); संख्या 422 (ए); नंबर 424 (बी); नंबर 426 पीपी 115-117।

सारांश (आकलन)।

प्रतिबिंब।

आइए समीकरणों के सिस्टम को ग्राफिक रूप से हल करने के लिए एल्गोरिथ्म को दोहराएं।

समीकरणों के एक निकाय के कितने हल हो सकते हैं?

समीकरणों के निकाय को आलेखीय रूप से हल करना किसने सीखा है?

किसने नहीं सीखा?

और कौन संदेह करता है?

हाथ उठाओ, सबक किसे पसंद आया? कौन नहीं करता? कौन उदासीन है?

गृहकार्य: 18 पीपी. 114-115 नियम सीखें।

17 पीपी.108-110 नियम दोहराएं।

वीडियो पाठ "समीकरण प्रणालियों को हल करने के लिए चित्रमय विधि" प्रस्तुत करता है शैक्षिक सामग्रीइस विषय का पता लगाने के लिए। सामग्री शामिल है सामान्य सिद्धांतसमीकरणों की एक प्रणाली को हल करने के बारे में, साथ ही विस्तृत विवरणउदाहरण के लिए कि कैसे समीकरणों की प्रणाली को ग्राफिक रूप से हल किया जाता है।

दृश्य सहायता निर्माण के अधिक सुविधाजनक और समझने योग्य निष्पादन के लिए एनीमेशन का उपयोग करती है, साथ ही विभिन्न तरीकेसामग्री की गहन समझ, बेहतर याद रखने के लिए महत्वपूर्ण अवधारणाओं और विवरणों को उजागर करना।

वीडियो ट्यूटोरियल विषय का परिचय देकर शुरू होता है। छात्रों को याद दिलाया जाता है कि समीकरणों की एक प्रणाली क्या है, और 7 वीं कक्षा में उन्हें पहले से ही समीकरणों की कौन सी प्रणाली से परिचित होना था। पहले, छात्रों को ax+by=c फॉर्म के समीकरणों के सिस्टम को हल करना होता था। समीकरणों की प्रणालियों को हल करने की अवधारणा को गहरा करने और उन्हें हल करने की क्षमता बनाने के लिए, इस वीडियो पाठ में दूसरी डिग्री के दो समीकरणों के साथ-साथ दूसरी डिग्री के एक समीकरण और दूसरे से मिलकर एक प्रणाली के समाधान पर चर्चा की गई है। - पहली डिग्री के। आपको याद दिलाता है कि समीकरणों की एक प्रणाली का समाधान क्या है। सिस्टम के समाधान की परिभाषा चर के मूल्यों की एक जोड़ी के रूप में होती है जो सही समानता में प्रतिस्थापित करते समय इसके समीकरणों को उलट देती है, स्क्रीन पर प्रदर्शित होती है। सिस्टम के समाधान की परिभाषा के अनुसार, कार्य निर्दिष्ट है। यह याद रखने के लिए स्क्रीन पर प्रदर्शित होता है कि किसी सिस्टम को हल करने का अर्थ है उपयुक्त समाधान खोजना या उनकी अनुपस्थिति को साबित करना।

समीकरणों की एक निश्चित प्रणाली को हल करने की चित्रमय पद्धति में महारत हासिल करने का प्रस्ताव है। समीकरण x 2 +y 2 =16 और y=-x 2 +2x+4 से मिलकर बने सिस्टम को हल करने के उदाहरण पर इस पद्धति के उपयोग पर विचार किया जाता है। सिस्टम का ग्राफिकल सॉल्यूशन इनमें से प्रत्येक समीकरण को प्लॉट करने से शुरू होता है। जाहिर है, समीकरण x 2 + y 2 \u003d 16 का ग्राफ एक वृत्त होगा। इस वृत्त से संबंधित बिंदु समीकरण का हल हैं। समीकरण के आगे, 4 की त्रिज्या वाला एक वृत्त मूल बिंदु पर O केंद्र के साथ समन्वय तल पर बनाया गया है। दूसरे समीकरण का ग्राफ एक परवलय है, जिसकी शाखाएँ नीचे की ओर होती हैं। यह परवलय समीकरण के ग्राफ के अनुरूप समन्वय तल पर निर्मित होता है। परवलय से संबंधित कोई भी बिंदु समीकरण y \u003d -x 2 + 2x + 4 का हल है। यह समझाया गया है कि समीकरणों की एक प्रणाली का समाधान उन ग्राफ़ पर बिंदु है जो एक साथ दोनों समीकरणों के ग्राफ़ से संबंधित हैं। इसका मतलब है कि निर्मित ग्राफ़ के प्रतिच्छेदन बिंदु समीकरणों की प्रणाली के समाधान होंगे।

यह ध्यान दिया जाता है कि ग्राफिकल विधि में दो ग्राफ़ के चौराहे पर स्थित बिंदुओं के निर्देशांक के अनुमानित मूल्य को खोजने में शामिल होता है, जो सिस्टम के प्रत्येक समीकरण के समाधान के सेट को दर्शाता है। यह आंकड़ा दो रेखांकन के पाए गए प्रतिच्छेदन बिंदुओं के निर्देशांक को चिह्नित करता है: ए, बी, सी, डी[-2;-3.5]। ये बिंदु ग्राफिक रूप से पाए गए समीकरणों की प्रणाली के समाधान हैं। आप उन्हें समीकरण में प्रतिस्थापित करके और निष्पक्ष समानता प्राप्त करके उनकी शुद्धता की जांच कर सकते हैं। बिंदुओं को समीकरण में प्रतिस्थापित करने के बाद, यह देखा जा सकता है कि कुछ बिंदु देते हैं सही मूल्यसमाधान, और भाग समीकरण के समाधान के अनुमानित मूल्य का प्रतिनिधित्व करता है: x 1 = 0, y 1 = 4; एक्स 2 \u003d 2, वाई 2 3.5; x 3 3.5, y 3 \u003d -2; एक्स 4 \u003d -2, वाई 4 -3.5।

वीडियो ट्यूटोरियल समीकरणों की एक प्रणाली को हल करने के लिए ग्राफिकल विधि के सार और अनुप्रयोग के बारे में विस्तार से बताता है। यह इस विषय का अध्ययन करते समय स्कूल में बीजगणित पाठ में वीडियो सहायता के रूप में इसका उपयोग करना संभव बनाता है। इसके अलावा, सामग्री के लिए उपयोगी होगा स्वयं अध्ययनछात्र और दूरस्थ शिक्षा में विषय को समझाने में मदद कर सकते हैं।