نقاط بحرانی تابع فواصل صعودی-کاهشی آنلاین هستند. افزایش و کاهش توابع، افراطی

عملکرد صعودی و کاهشی

عملکرد y = f(ایکس) افزایش در بخش [ آ, ب]، اگر برای هر جفت نقطه ایکسو ایکس", a ≤ x، نابرابری f(ایکس) ≤ f (ایکس"، و به شدت افزایش می یابد - اگر نابرابری f (ایکس) f(ایکس"). کاهش و کاهش شدید یک تابع به طور مشابه تعریف می شود. به عنوان مثال، تابع در = ایکس 2 (برنج. ، الف) به شدت در بخش افزایش می یابد، و

(برنج. ، ب) در این فاصله به شدت کاهش می یابد. توابع افزایشی نشان داده می شوند f (ایکس) و کاهش می یابد f (ایکس)↓. به منظور یک تابع متمایز f (ایکس) در بازه زمانی [ آ, ب]، لازم و کافی است که مشتق آن f"(ایکس) غیر منفی بود در [ آ, ب].

همراه با افزایش و کاهش یک تابع در یک قطعه، افزایش و کاهش یک تابع در یک نقطه در نظر گرفته می شود. عملکرد در = f (ایکس) در نقطه افزایش نامیده می شود ایکس 0 اگر چنین بازه ای (α، β) حاوی نقطه وجود داشته باشد ایکس 0، که برای هر نقطه ایکساز (α، β)، x> ایکس 0، نابرابری f (ایکس 0) ≤ f (ایکس) و برای هر نقطه ایکساز (α، β)، x 0، نابرابری f (ایکس) ≤ f (ایکس 0). افزایش شدید یک تابع در یک نقطه به طور مشابه تعریف می شود ایکس 0 . اگر یک f"(ایکس 0) > 0، سپس تابع f(ایکس) در نقطه به شدت در حال افزایش است ایکس 0 . اگر یک f (ایکس) در هر نقطه از بازه افزایش می یابد ( آ, ب، سپس در این بازه افزایش می یابد.

اس بی استکین.

بزرگ دایره المعارف شوروی. - م.: دایره المعارف شوروی. 1969-1978 .

ببینید «عملکرد افزایش و کاهش» در فرهنگ‌های دیگر چیست:

مفاهیم تجزیه و تحلیل ریاضی. تابع f(x) در بخش ساختار سنی جمعیت، نسبت تعداد گروه‌های سنی مختلف جمعیت افزایش می‌یابد. بستگی به میزان تولد و مرگ، امید به زندگی افراد دارد... فرهنگ لغت دایره المعارفی بزرگ

مفاهیم تحلیل ریاضی. تابع f(x) در بازه افزایشی نامیده می شود اگر برای هر جفت نقطه x1 و x2، a≤x1 ... فرهنگ لغت دایره المعارفی

مفاهیم ریاضی. تحلیل و بررسی. تابع f(x) فراخوانی شد. افزایش در بخش [a, b]، اگر برای هر جفت نقطه x1 و x2، و<или=х1 <х<или=b, выполняется неравенство f(x1)علوم طبیعی. فرهنگ لغت دایره المعارفی

شاخه ای از ریاضیات که مشتقات و دیفرانسیل توابع و کاربردهای آنها را در مطالعه توابع مطالعه می کند. ثبت نام د. به یک رشته ریاضی مستقل با نام های I. Newton و G. Leibniz مرتبط است (نیمه دوم 17 ... دایره المعارف بزرگ شوروی

شاخه ای از ریاضیات که در آن مفاهیم مشتق و دیفرانسیل و نحوه به کارگیری آنها در مطالعه توابع مطالعه می شود. توسعه D. و. ارتباط نزدیکی با توسعه حساب انتگرال دارد. جدایی ناپذیر و محتوای آنها. آنها با هم اساس ... دایره المعارف ریاضی

این اصطلاح معانی دیگری دارد، به تابع مراجعه کنید. درخواست "نمایش" به اینجا هدایت می شود. معانی دیگر را نیز ببینید ... ویکی پدیا

ارسطو و مشائیان- پرسش ارسطویی زندگی ارسطو ارسطو در سال 384/383 متولد شد. قبل از میلاد مسیح ه. در استاگیرا، در مرز مقدونیه. پدرش که نیکوماخوس نام داشت، پزشکی در خدمت آمینتاس پادشاه مقدونی، پدر فیلیپ بود. ارسطو جوان به همراه خانواده اش ... فلسفه غرب از پیدایش تا امروز

- (QCD)، نظریه میدان کوانتومی برخورد قوی کوارک ها و گلوئون ها، ساخته شده در تصویر کوانتومی. الکترودینامیک (QED) بر اساس تقارن سنج "رنگ". بر خلاف QED، فرمیون ها در QCD دارای مکمل هستند. کوانتوم درجه آزادی عدد،… … دایره المعارف فیزیکی

I Heart قلب (لاتین کور، یونانی کاردیا) اندام فیبروموزولی توخالی است که به عنوان یک پمپ عمل می کند و حرکت خون را در سیستم گردش خون تضمین می کند. آناتومی قلب در مدیاستن قدامی (mediastinum) در پریکارد بین ... ... دایره المعارف پزشکی

زندگی یک گیاه، مانند زندگی هر موجود زنده دیگری، مجموعه پیچیده ای از فرآیندهای مرتبط است. مهمترین آنها، همانطور که مشخص است، تبادل مواد با محیط است. محیط زیست منبعی است که از آن ...... دایره المعارف زیستی

برای تعیین ماهیت یک تابع و صحبت در مورد رفتار آن، باید فواصل افزایش و کاهش را پیدا کرد. این فرآیند کاوش و رسم تابع نامیده می شود. نقطه افراطی هنگام یافتن بزرگترین و کوچکترین مقادیر تابع استفاده می شود، زیرا آنها تابع را از بازه افزایش یا کاهش می دهند.

این مقاله تعاریف را نشان می دهد، ما فرموله می کنیم علامت کافیافزایش و کاهش در فاصله و شرط وجود افراط. این برای حل مثال ها و مسائل صدق می کند. بخش تمایز توابع باید تکرار شود، زیرا هنگام حل باید از یافتن مشتق استفاده شود.

Yandex.RTB R-A-339285-1 تعریف 1

تابع y = f (x) در بازه x زمانی افزایش می یابد که برای هر x 1 ∈ X و x 2 ∈ X , x 2 > x 1 نابرابری f (x 2) > f (x 1) امکان پذیر باشد. به عبارت دیگر، مقدار بزرگتر آرگومان با مقدار بزرگتر تابع مطابقت دارد.

تعریف 2

وقتی برای هر x 1 ∈ X , x 2 ∈ X , x 2 > x 1 برابری f (x 2) > f (x 1) در نظر گرفته می شود، تابع y = f (x) در بازه x کاهش می یابد. شدنی. به عبارت دیگر، یک مقدار تابع بزرگتر با یک مقدار آرگومان کوچکتر مطابقت دارد. شکل زیر را در نظر بگیرید.

اظهار نظر: وقتی تابع در انتهای بازه صعودی و نزولی مشخص و پیوسته باشد، یعنی (a; b) که در آن x = a، x = b، نقاط در بازه صعودی و نزولی قرار می گیرند. این با تعریف مغایرتی ندارد، به این معنی که در بازه x رخ می دهد.

ویژگی های اصلی توابع ابتدایی از نوع y = sin x قطعیت و پیوستگی برای مقادیر واقعی آرگومان ها است. از اینجا دریافتیم که افزایش سینوس در بازه - π 2 اتفاق می افتد. π 2 ، سپس افزایش در بخش به شکل - π 2 است. π 2 .

نقطه x 0 نامیده می شود حداکثر امتیازبرای یک تابع y = f (x) زمانی که برای همه مقادیر x نابرابری f (x 0) ≥ f (x) درست است. حداکثر ویژگیمقدار تابع در نقطه است و با y m a x نشان داده می شود.

نقطه x 0 حداقل نقطه برای تابع y \u003d f (x) نامیده می شود که برای همه مقادیر x نابرابری f (x 0) ≤ f (x) درست باشد. حداقل ویژگیمقدار تابع در نقطه است و دارای شکل y m i n است.

همسایگی نقطه x 0 در نظر گرفته می شود نقاط افراطی،و مقدار تابعی که مربوط به نقاط انتهایی است. شکل زیر را در نظر بگیرید.

منتهی تابع با بزرگترین و با کوچکترین مقدارکارکرد. شکل زیر را در نظر بگیرید.

تصویر اول می گوید که چه چیزی باید پیدا شود بالاترین ارزشتوابع از بخش [a; ب]. با استفاده از حداکثر نقاط پیدا می شود و برابر با حداکثر مقدار تابع است، و شکل دوم بیشتر شبیه یافتن یک نقطه حداکثر در x = b است.

شرایط کافی برای افزایش و کاهش توابع

برای یافتن ماکزیمم و مینیمم یک تابع، در صورتی که تابع این شرایط را داشته باشد، باید علائم یک اکستروم را اعمال کرد. اولین ویژگی رایج ترین مورد استفاده است.

اولین شرط کافی برای افراط

اجازه دهید یک تابع y = f (x) داده شود که در همسایگی ε نقطه x 0 قابل تفکیک است و در نقطه داده شده x 0 پیوستگی دارد. از این رو ما آن را دریافت می کنیم

• وقتی f "(x) > 0 با x ∈ (x 0 - ε; x 0) و f" (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• وقتی f"(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 برای x ∈ (x 0 ; x 0 + ε) , سپس x 0 حداقل نقطه است.

به عبارت دیگر، شرایط تنظیم علامت آنها را به دست می آوریم:

• هنگامی که تابع در نقطه x 0 پیوسته است، آنگاه مشتقی با علامت متغیر دارد، یعنی از + به -، به این معنی که نقطه حداکثر نامیده می شود.
• هنگامی که تابع در نقطه x 0 پیوسته است، آنگاه مشتقی با علامت تغییر از - به + دارد، به این معنی که نقطه حداقل نامیده می شود.

برای تعیین صحیح حداکثر و حداقل نقاط تابع، باید الگوریتم پیدا کردن آنها را دنبال کنید:

• دامنه تعریف را پیدا کنید.
• مشتق تابع در این ناحیه را پیدا کنید.
• شناسایی صفرها و نقاطی که تابع وجود ندارد.
• تعیین علامت مشتق در فواصل.
• نقاطی را انتخاب کنید که تابع علامت آن را تغییر می دهد.

الگوریتم مثال حل چند مثال از یافتن منتهی الیه تابع را در نظر بگیرید.

مثال 1

نقاط بالا و پایین را پیدا کنید عملکرد داده شده y = 2 (x + 1) 2 x - 2 .

راه حل

دامنه این تابع همه اعداد حقیقی به جز x = 2 است. ابتدا مشتق تابع را پیدا می کنیم و به دست می آوریم:

y "= 2 x + 1 2 x - 2" = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2)" (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2)) - (x + 2) 2 (x - 2) 2 = = 2 (x + 1) (x - 5) (x - 2) 2

از اینجا می بینیم که صفرهای تابع x \u003d - 1، x \u003d 5، x \u003d 2 هستند، یعنی هر براکت باید برابر با صفر باشد. روی خط شماره علامت بزنید و دریافت کنید:

حال از هر بازه نشانه های مشتق را مشخص می کنیم. لازم است نقطه ای را انتخاب کنید که در فاصله وجود دارد، آن را در عبارت جایگزین کنید. به عنوان مثال، نقاط x = - 2، x = 0، x = 3، x = 6.

ما آن را دریافت می کنیم

y "(- 2) \u003d 2 (x + 1) (x - 5) (x - 2) 2 x \u003d - 2 \u003d 2 (- 2 + 1) (- 2 - 5) (- 2 - 2 ) 2 \u003d 2 7 16 \u003d 7 8 > 0، بنابراین، بازه - ∞؛ - 1 دارای مشتق مثبت است. به طور مشابه، ما به دست می آوریم که

y "(0) = 2 (0 + 1) 0 - 5 0 - 2 2 = 2 - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

از آنجایی که فاصله دوم کمتر از صفر است، به این معنی است که مشتق روی بخش منفی خواهد بود. سومی با منفی، چهارمی با مثبت. برای تعیین تداوم، باید به علامت مشتق توجه شود، اگر تغییر کند، این یک نقطه افراطی است.

ما دریافتیم که در نقطه x = - 1 تابع پیوسته خواهد بود، به این معنی که مشتق علامت + به - را تغییر می دهد. با توجه به علامت اول داریم که x = - 1 حداکثر نقطه است، یعنی به دست می آوریم

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

نقطه x = 5 نشان می دهد که تابع پیوسته است و مشتق علامت - را به + تغییر می دهد. از این رو، x=-1 حداقل نقطه است و یافته آن شکل دارد

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

تصویر گرافیکی

پاسخ: y m a x = y (- 1) = 0، y m i n = y (5) = 24.

شایان توجه است که استفاده از اولین علامت کافی یک اکسترموم نیازی به تمایز تابع از نقطه x 0 ندارد و این امر محاسبه را ساده می کند.

مثال 2

حداکثر و حداقل نقاط تابع y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 را بیابید.

راه حل.

دامنه یک تابع همه اعداد حقیقی است. این را می توان به عنوان یک سیستم معادلات به شکل زیر نوشت:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

سپس باید مشتق را پیدا کنید:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

نقطه x = 0 هیچ مشتقی ندارد، زیرا مقادیر حدود یک طرفه متفاوت است. دریافتیم که:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y "x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

نتیجه این است که تابع در نقطه x = 0 پیوسته است، سپس محاسبه می کنیم

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 (0 - 0) 3 - 2 (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 ( 0 + 0) 2 + 22 3 (0 + 0) - 8 = - 8 سال (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

برای یافتن مقدار آرگومان در زمانی که مشتق صفر می شود، باید محاسبات انجام شود:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3، x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

تمام نقاط به دست آمده باید روی خط علامت گذاری شوند تا علامت هر بازه مشخص شود. بنابراین، محاسبه مشتق در نقاط دلخواه برای هر بازه ضروری است. به عنوان مثال، می توانیم نقاطی را با مقادیر x = - 6، x = - 4، x = - 1، x = 1، x = 4، x = 6 بگیریم. ما آن را دریافت می کنیم

y " (- 6) \u003d - 1 2 x 2 - 4 x - 22 3 x \u003d - 6 \u003d - 1 2 - 6 2 - 4 (- 6) - 22 3 \u003d - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

تصویر روی یک خط مستقیم دارای فرم است

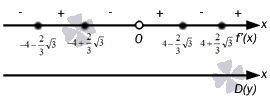
پس به این نکته می رسیم که باید به اولین علامت افراط متوسل شد. ما محاسبه می کنیم و آن را می گیریم

x = - 4 - 2 3 3، x = 0، x = 4 + 2 3 3، سپس از اینجا حداکثر نقاط دارای مقادیر x = - 4 + 2 3 3، x = 4 - 2 3 3 هستند.

بیایید به محاسبه حداقل ها برویم:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

اجازه دهید ماکزیمم تابع را محاسبه کنیم. ما آن را دریافت می کنیم

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

تصویر گرافیکی

پاسخ:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 m 27 x3 = y 4 - 2 3 3 = 8 27 3

اگر تابع f "(x 0) = 0 داده شود، با f "" آن (x 0) > 0 دریافت می کنیم که x 0 حداقل نقطه است اگر f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

مثال 3

ماکزیمم و مینیمم تابع y = 8 x x + 1 را بیابید.

راه حل

ابتدا دامنه تعریف را پیدا می کنیم. ما آن را دریافت می کنیم

D (y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

لازم است تابع را متمایز کنیم، پس از آن به دست می آوریم

y "= 8 x x + 1" = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

هنگامی که x = 1، مشتق برابر با صفر می شود، که به این معنی است که نقطه یک انتها ممکن است. برای روشن شدن، لازم است مشتق دوم را پیدا کنید و مقدار x \u003d 1 را محاسبه کنید. ما گرفتیم:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x "(x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x "(x + 1) 4 x == 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 - 4 8 = - 1< 0

بنابراین، با استفاده از 2 شرایط کافی extremum، دریافت می کنیم که x = 1 حداکثر نقطه است. در غیر این صورت، ورودی y m a x = y (1) = 8 1 1 + 1 = 4 است.

تصویر گرافیکی

پاسخ: y m a x = y (1) = 4 ..

تابع y = f (x) مشتق آن تا مرتبه n در همسایگی ε نقطه داده شده x 0 و مشتق آن تا مرتبه n + 1 در نقطه x 0 است. سپس f "(x 0) = f "" (x 0) = f "" " (x 0) = . . . = f n (x 0) = 0 .

نتیجه این است که وقتی n یک عدد زوج باشد، x 0 نقطه عطف در نظر گرفته می شود، زمانی که n یک عدد فرد باشد، x 0 یک نقطه منتهی است، و f (n + 1) (x 0) > 0، سپس x 0 یک حداقل نقطه است، f(n+1)(x0)< 0 , тогда x 0 является точкой максимума.

مثال 4

حداکثر و حداقل نقاط تابع y y = 1 16 (x + 1) 3 (x - 3) 4 را بیابید.

راه حل

تابع اصلی یک تابع کاملاً گویا است، از این رو نتیجه می شود که دامنه تعریف همه اعداد حقیقی است. تابع باید متمایز شود. ما آن را دریافت می کنیم

y "= 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " == 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

این مشتق در x 1 = - 1، x 2 = 5 7، x 3 = 3 به صفر می رسد. یعنی نقاط می توانند نقاط یک افراطی احتمالی باشند. لازم است سومین شرط اکستریم کافی را اعمال کرد. یافتن مشتق دوم به شما امکان می دهد تا حضور حداکثر و حداقل یک تابع را به دقت تعیین کنید. مشتق دوم در نقاط انتهایی احتمالی آن محاسبه می شود. ما آن را دریافت می کنیم

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

این بدان معنی است که x 2 \u003d 5 7 حداکثر نقطه است. با اعمال 3 معیار کافی، به دست می آوریم که برای n = 1 و f (n + 1) 5 7< 0 .

تعیین ماهیت نقاط x 1 = - 1، x 3 = 3 ضروری است. برای انجام این کار، شما باید مشتق سوم را پیدا کنید، مقادیر را در این نقاط محاسبه کنید. ما آن را دریافت می کنیم

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " == 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y "" " (- 1) = 96 ≠ 0 y " "" (3) = 0

بنابراین، x 1 = - 1 نقطه عطف تابع است، زیرا برای n = 2 و f (n + 1) (- 1) ≠ 0. بررسی نقطه x 3 = 3 ضروری است. برای انجام این کار، مشتق چهارم را پیدا کرده و در این مرحله محاسبات را انجام می دهیم:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " == 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

از موارد فوق نتیجه می گیریم که x 3 \u003d 3 حداقل نقطه تابع است.

تصویر گرافیکی

پاسخ: x 2 \u003d 5 7 حداکثر نقطه است، x 3 \u003d 3 - حداقل نقطه تابع داده شده است.

اگر متوجه اشتباهی در متن شدید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

کار فارغ التحصیلی در قالب آزمون یکپارچه ایالتی برای دانش آموزان کلاس 11 لزوماً شامل وظایفی برای محاسبه حدود ، فواصل کاهش و افزایش مشتق یک تابع ، یافتن نقاط افراطی و رسم نمودارها است. دانش خوباین مبحث به شما امکان می دهد به درستی به چندین سوال امتحان پاسخ دهید و در آموزش حرفه ای بیشتر با مشکل مواجه نشوید.

مبانی حساب دیفرانسیل - یکی از موضوعات اصلی ریاضیات مدرسه مدرن. او استفاده از مشتق را برای مطالعه وابستگی های متغیرها مطالعه می کند - از طریق مشتق است که می توانید افزایش و کاهش یک تابع را بدون مراجعه به نقشه تجزیه و تحلیل کنید.

آمادگی همه جانبه فارغ التحصیلان برای قبولی در امتحانبر روی پورتال آموزشی"Skolkovo" به درک عمیق اصول تمایز کمک می کند - برای درک دقیق تئوری، مطالعه نمونه هایی از حل مشکلات معمولی و تلاش خود در کار مستقل. ما به شما کمک خواهیم کرد تا شکاف های دانش را از بین ببرید - درک خود را از مفاهیم واژگانی موضوع و وابستگی های کمیت ها روشن کنید. دانش‌آموزان می‌توانند نحوه یافتن بازه‌های یکنواختی را تکرار کنند، که به معنای افزایش یا سقوط مشتق یک تابع در بازه‌ای معین است، زمانی که نقاط مرزی شامل می‌شوند و در فواصل یافت‌شده لحاظ نمی‌شوند.

قبل از شروع حل مستقیم مسائل موضوعی، توصیه می کنیم ابتدا به قسمت «مرجع نظری» رفته و تعاریف مفاهیم، ​​قواعد و فرمول های جدولی را تکرار کنید. در اینجا می توانید نحوه یافتن و ثبت هر بازه توابع افزایش و کاهش را در نمودار مشتق نیز مطالعه کنید.

تمام اطلاعات ارائه شده به در دسترس ترین شکل برای درک عملی از ابتدا ارائه شده است. این سایت مطالبی را برای درک و جذب در چندین ارائه می دهد اشکال گوناگون– خواندن، مشاهده ویدئو و آموزش مستقیم تحت راهنمایی معلمان با تجربه. مربیان حرفه ایبه تفصیل بگویید چگونه فواصل افزایش و کاهش مشتق یک تابع را با روش تحلیلی و راه های گرافیکی. در طول وبینارها، امکان طرح هر گونه سوال مورد علاقه هم در تئوری و هم در حل مسائل خاص وجود خواهد داشت.

با یادآوری نکات اصلی مبحث، به مثال هایی از افزایش مشتق یک تابع، مشابه وظایف نگاه کنید گزینه های امتحان. برای تثبیت آنچه یاد گرفته اید، به "کاتالوگ" نگاه کنید - در اینجا تمرین های عملی برای کار مستقل. وظایف در بخش انتخاب شده است سطوح مختلفمشکل از نظر توسعه مهارت. برای هر یک از آنها، به عنوان مثال، الگوریتم های حل و پاسخ های صحیح پیوست شده است.

با انتخاب بخش "سازنده"، دانش آموزان می توانند مطالعه افزایش و کاهش مشتق یک تابع در واقعی را تمرین کنند. از گزینه های استفاده کنید، به طور مداوم با در نظر گرفتن به روز رسانی می شود تغییرات اخیرو نوآوری

مشتق. اگر مشتق یک تابع برای هر نقطه از بازه مثبت باشد، آن تابع در حال افزایش است و اگر منفی باشد کاهش می یابد.

برای یافتن فواصل افزایش و کاهش یک تابع، باید دامنه تعریف آن، مشتق را پیدا کنید، نامساوی‌های شکل F’(x) > 0 و F’(x) را حل کنید.

راه حل.

3. نابرابری های y’ > 0 و y’ 0 را حل کنید.
(4 - x)/x³

راه حل.
1. دامنه تابع را پیدا کنید. بدیهی است که عبارت در مخرج باید همیشه با صفر متفاوت باشد. بنابراین، 0 از دامنه تعریف حذف می شود: تابع برای x ∈ (-∞; 0)∪(0; +∞) تعریف شده است.

2. مشتق تابع را محاسبه کنید:
y'(x) = ((3 x² + 2 x - 4)' x² – (3 x² + 2 x - 4) (x²)')/x^4 = ((6 x + 2) x² - (3 x²) + 2 x - 4) 2 x) / x^4 = (6 x³ + 2 x² - 6 x³ - 4 x² + 8 x) / x^ 4 \u003d (8 x - 2 x²) / x ^ 4 \u003d 2 (4 - x) / x³.

3. نابرابری های y’ > 0 و y’ 0 را حل کنید.
(4 - x)/x³

4. سمت چپ نابرابری یک x = 4 واقعی دارد و در x = 0 تبدیل می شود. بنابراین، مقدار x = 4 در بازه و در بازه کاهش قرار می گیرد و نقطه 0 لحاظ نمی شود.
بنابراین، تابع مورد نیاز در بازه x ∈ (-∞؛ 0) ∪ افزایش می یابد.

4. سمت چپ نابرابری یک x = 4 واقعی دارد و در x = 0 تبدیل می شود. بنابراین، مقدار x = 4 در بازه و در بازه کاهش قرار می گیرد و نقطه 0 لحاظ نمی شود.
بنابراین، تابع مورد نیاز در بازه x ∈ (-∞؛ 0) ∪ افزایش می یابد.

منابع:

• چگونه فواصل کاهشی یک تابع را پیدا کنیم

تابع وابستگی شدید یک عدد به عدد دیگر یا مقدار تابع (y) به آرگومان (x) است. هر فرآیند (نه تنها در ریاضیات) را می توان با عملکرد خود توصیف کرد، که خواهد داشت مشخصات: فواصل کاهش و افزایش، نقاط حداقل و حداکثر و غیره.

شما نیاز خواهید داشت

• - کاغذ؛
• - یک خودکار.

دستورالعمل

مثال 2
فواصل کاهش f(x)=sinx +x را بیابید.
مشتق این تابع برابر خواهد بود با: f'(x)=cosx+1.
حل نابرابری cosx+1

فاصله یکنواختییک تابع را می توان بازه ای نامید که در آن تابع یا فقط افزایش می یابد یا فقط کاهش می یابد. تعدادی از اقدامات خاص به یافتن چنین محدوده هایی برای یک تابع کمک می کند، که اغلب در مسائل جبری از این نوع مورد نیاز است.

دستورالعمل

اولین قدم در حل مسئله تعیین فواصل زمانی که تابع به صورت یکنواخت افزایش یا کاهش می یابد، محاسبه این تابع است. برای انجام این کار، تمام مقادیر آرگومان ها (مقادیر روی محور x) را پیدا کنید که می توانید مقدار تابع را برای آنها پیدا کنید. نقاطی را که شکاف ها مشاهده می شود علامت بزنید. مشتق تابع را بیابید. پس از تعریف عبارتی که مشتق را نشان می دهد، آن را با صفر برابر کنید. پس از آن، شما باید ریشه های حاصل را پیدا کنید. در مورد مساحت مجاز نیست.

نقاطی که تابع یا مشتق آن برابر با صفر است، مرزهای فواصل هستند. یکنواختی. این محدوده ها و همچنین نقاط جدا کننده آنها باید به ترتیب در جدول وارد شوند. علامت مشتق تابع را در فواصل بدست آمده بیابید. برای انجام این کار، هر آرگومان از بازه را با عبارت مربوط به مشتق جایگزین کنید. اگر نتیجه مثبت باشد، تابع در این محدوده افزایش می یابد، در غیر این صورت کاهش می یابد. نتایج در یک جدول وارد می شود.

خط نشان دهنده مشتق تابع f'(x) مطابق با مقادیر آرگومان ها نوشته می شود: "+" - اگر مشتق مثبت باشد، "-" - منفی یا "0" - برابر با صفر است. در خط بعدی به یکنواختی خود عبارت اصلی توجه کنید. فلش بالا مربوط به افزایش است، فلش پایین مربوط به کاهش است. ویژگی ها را بررسی کنید. اینها نقاطی هستند که مشتق آن صفر است. یک افراط می تواند یک نقطه بالا یا یک نقطه پایین باشد. اگر بخش قبلی تابع در حال افزایش بود و قسمت فعلی در حال کاهش است، این حداکثر نقطه است. در حالتی که تابع تا یک نقطه معین کاهش می‌یابد و اکنون در حال افزایش است، این حداقل نقطه است. مقادیر تابع را در نقاط انتهایی جدول وارد کنید.

منابع:

• تعریف یکنواختی چیست؟

مطالعه رفتار تابعی که وابستگی پیچیده ای به آرگومان دارد با استفاده از مشتق انجام می شود. با توجه به ماهیت تغییر در مشتق، می توان نقاط بحرانی و مناطق رشد یا کاهش تابع را یافت.

"عملکرد افزایش و کاهش"

اهداف درس:

1. یاد بگیرید که فواصل یکنواختی را پیدا کنید.

2. توسعه توانایی های ذهنی که تجزیه و تحلیل موقعیت و توسعه روش های عمل کافی (تحلیل، سنتز، مقایسه) را ارائه می دهد.

3. شکل گیری علاقه به موضوع.

امروز ما به مطالعه کاربرد مشتق ادامه می دهیم و مسئله کاربرد آن در مطالعه توابع را بررسی می کنیم. کار جلو

و حالا بیایید تعاریفی از ویژگی های تابع "Brainstorm" ارائه کنیم

1. به چه چیزی تابع گفته می شود؟

2. نام متغیر x چیست؟

3. نام متغیر Y چیست؟

4. محدوده یک تابع چقدر است؟

5. مجموعه مقدار تابع چیست؟

6. تابع زوج چیست؟

7. کدام تابع فرد نامیده می شود؟

8. در مورد نمودار یک تابع زوج چه می توان گفت؟

9. در مورد نمودار یک تابع فرد چه می توان گفت؟

10. تابع افزایشی چیست؟

11. تابع کاهشی چیست؟

12. تابع تناوبی چیست؟

ریاضیات مدل های ریاضی را مطالعه می کند. یکی از مهمترین مدل های ریاضییک تابع است. وجود داشته باشد روش های مختلفتوضیحات عملکرد کدام یک واضح تر است؟

- گرافیک

- چگونه یک نمودار بسازیم؟

- با امتیاز.

این روش در صورتی مناسب است که از قبل بدانید نمودار چگونه است. مثلاً نمودار چیست تابع درجه دوم, تابع خطی, نسبت معکوس، توابع y = sinx؟ (فرمول های مربوطه نشان داده می شوند، دانش آموزان منحنی هایی را که نمودار هستند نام می برند.)

اما اگر بخواهید یک تابع یا حتی پیچیده تر را نمودار کنید، چه؟ شما می توانید چندین نقطه را پیدا کنید، اما عملکرد عملکرد بین این نقاط چگونه است؟

دو نقطه را روی تخته قرار دهید، از دانش آموزان بخواهید نشان دهند که نمودار "بین آنها" چگونه می تواند باشد:

برای اینکه بفهمید یک تابع چگونه رفتار می کند، مشتق آن کمک می کند.

دفترچه ها را باز کنید، عدد را یادداشت کنید، کار کلاسی.

هدف از درس: بیاموزید که چگونه نمودار یک تابع با نمودار مشتق آن مرتبط است و یاد بگیرید که چگونه مسائل دو نوع را حل کنید:

1. با توجه به نمودار مشتق، فواصل افزایش و کاهش خود تابع و همچنین نقاط انتهایی تابع را بیابید.

2. با توجه به طرح نشانه های مشتق بر روی فواصل، فواصل افزایش و کاهش خود تابع و همچنین نقاط انتهایی تابع را بیابید.

در کتاب های درسی ما چنین تکالیفی وجود ندارد، اما در تست های تک پیدا می شوند آزمون دولتی(قسمت الف و ب).

امروز در درس ما یک عنصر کوچک از کار مرحله دوم مطالعه فرآیند را در نظر خواهیم گرفت، مطالعه یکی از ویژگی های تابع - تعیین فواصل یکنواختی

برای حل این مشکل، لازم است برخی از مواردی که قبلاً مطرح شد را یادآور شویم.

پس بیایید مبحث درس امروز را بنویسیم: نشانه های توابع افزایش و کاهش.

علائم افزایش و کاهش عملکرد:

اگر مشتق این تابع برای تمام مقادیر x در بازه (a; c)، یعنی f "(x)\u003e 0 مثبت باشد، تابع در این بازه افزایش می یابد.
اگر مشتق این تابع برای تمام مقادیر x در بازه (a; b) منفی باشد، یعنی f "(x)< 0, то функция в этом интервале убывает

ترتیب یافتن فواصل یکنواختی:

محدوده تابع را پیدا کنید.

1. اولین مشتق تابع را پیدا کنید.

2. در هیئت مدیره تصمیم گیری کنید

نقاط بحرانی را پیدا کنید، علامت اولین مشتق را در فواصل زمانی که نقاط بحرانی یافت شده دامنه تابع را تقسیم می کنند، بررسی کنید. فواصل یکنواختی توابع را پیدا کنید:

الف) حوزه تعریف،

ب) مشتق اول را بیابید:

ج) نقاط بحرانی را پیدا کنید: ، و

3. علامت مشتق را در فواصل به دست آمده بررسی می کنیم، راه حل به صورت جدول ارائه شده است.

به نقاط افراطی اشاره کنید

بیایید به چند نمونه از بررسی یک تابع برای افزایش و کاهش نگاه کنیم.

شرط کافی برای وجود حداکثر تغییر علامت مشتق هنگام عبور از نقطه بحرانی از "+" به "-" و برای حداقل از "-" به "+" است. اگر مشتق هنگام عبور از نقطه بحرانی علامت تغییر نکند، در این نقطه اکسترومی وجود ندارد.

1. D(f) را پیدا کنید.

2. f "(x) را پیدا کنید.

3. نقاط ثابت را پیدا کنید، یعنی. نقاطی که f"(x) = 0 یا f"(x) وجود ندارد.
(مشتق در صفرهای صورت 0 است، مشتق در صفرهای مخرج وجود ندارد)

4. D(f) و این نقاط را روی خط مختصات قرار دهید.

5. نشانه های مشتق را در هر یک از فواصل مشخص کنید

6. علائم را اعمال کنید.

7. پاسخ را یادداشت کنید.

ادغام مواد جدید.

دانش آموزان دوتایی کار می کنند و راه حل های خود را در دفترچه یادداشت خود می نویسند.

الف) y \u003d x³ - 6 x² + 9 x - 9؛

ب) y \u003d 3 x² - 5x + 4.

دو نفر روی تخته سیاه کار می کنند.

الف) y \u003d 2 x³ - 3 x² - 36 x + 40

ب) y \u003d x4-2 x³

3.خلاصه درس

تکلیف: تست (متمایز)