Кои матрици имат обратна. обратна матрица

Тази тема е една от най-омразните сред студентите. По-лошо, вероятно, само детерминанти.

Номерът е, че самата концепция за обратния елемент (и сега не говоря само за матрици) ни препраща към операцията умножение. Дори в училищна програмасе разглежда умножението сложна операция, а умножението на матрици като цяло е отделна тема, на която имам цял параграф и видео урок, посветен на нея.

Днес няма да навлизаме в детайлите на матричните изчисления. Само запомнете: как се обозначават матриците, как се умножават и какво следва от това.

Преглед: Матрично умножение

Първо, нека се споразумеем за нотацията. Матрица $A$ с размер $\left[ m\times n \right]$ е просто таблица с числа с точно $m$ реда и $n$ колони:

\=\под скоба(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrix) \right])_(n)\]

За да не объркате случайно редове и колони на места (повярвайте ми, на изпита можете да объркате един с двойка - какво да кажем за някои редове там), просто погледнете снимката:

Определяне на индекси за матрични клетки

Какво се случва? Ако поставим стандартната координатна система $OXY$ в горния ляв ъгъл и насочим осите така, че да покриват цялата матрица, тогава всяка клетка от тази матрица може да бъде уникално свързана с координатите $\left(x;y \right) $ - това ще бъде номера на реда и номера на колоната.

Защо координатната система е поставена точно в горния ляв ъгъл? Да, защото именно оттам започваме да четем всякакви текстове. Много лесно се запомня.

Защо оста $x$ сочи надолу, а не надясно? Отново е просто: вземете стандартната координатна система (оста $x$ върви надясно, оста $y$ върви нагоре) и я завъртете така, че да обхваща матрицата. Това е завъртане на 90 градуса по часовниковата стрелка - виждаме резултата от него на снимката.

Като цяло разбрахме как да определим индексите на матричните елементи. Сега нека се заемем с умножението.

Определение. Матриците $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когато броят на колоните в първата съответства на броя на редовете във втората, са наречена последователна.

В този ред е. Човек може да бъде двусмислен и да каже, че матриците $A$ и $B$ образуват подредена двойка $\left(A;B \right)$: ако те са последователни в този ред, тогава изобщо не е необходимо $B $ и $A$, тези. двойката $\left(B;A \right)$ също е последователна.

Само последователни матрици могат да бъдат умножени.

Определение. Произведението на последователни матрици $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ е новата матрица $C=\left[ m\times k \right ]$ , чиито елементи $((c)_(ij))$ се изчисляват по формулата:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

С други думи: за да получите елемента $((c)_(ij))$ на матрицата $C=A\cdot B$, трябва да вземете $i$-реда на първата матрица, $j$ -та колона на втората матрица и след това умножете по двойки елементи от този ред и колона. Съберете резултатите.

Да, това е сурово определение. От него веднага следват няколко факта:

1. Матричното умножение е, най-общо казано, некомутативно: $A\cdot B\ne B\cdot A$;
2. Умножението обаче е асоциативно: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. И дори разпределителен: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. И отново дистрибутив: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Дистрибутивността на умножението трябваше да бъде описана отделно за левия и десния умножител-сума само поради некомутативността на операцията за умножение.

Ако въпреки това се окаже, че $A\cdot B=B\cdot A$, такива матрици се наричат ​​пермутабилни.

Сред всички матрици, които се умножават по нещо там, има специални - тези, които, когато се умножат по произволна матрица $A$, отново дават $A$:

Определение. Матрица $E$ се нарича идентичност, ако $A\cdot E=A$ или $E\cdot A=A$. В случай на квадратна матрица $A$ можем да запишем:

Идентификационната матрица е чест гост при решаването матрични уравнения. И като цяло, чест гост в света на матриците. :)

И заради това $E$ някой измисли цялата игра, която ще бъде написана по-нататък.

Какво е обратна матрица

Тъй като умножението на матрицата е много отнемаща време операция (трябва да умножите куп редове и колони), концепцията за обратна матрица също не е най-тривиалната. И има нужда от някакво обяснение.

Ключова дефиниция

Е, време е да разберем истината.

Определение. Матрицата $B$ се нарича обратна на матрицата $A$ ако

Обратната матрица се обозначава с $((A)^(-1))$ (да не се бърка със степента!), така че определението може да бъде пренаписано по следния начин:

Изглежда, че всичко е изключително просто и ясно. Но когато се анализира такова определение, веднага възникват няколко въпроса:

1. Винаги ли съществува обратна матрица? И ако не винаги, тогава как да се определи: кога съществува и кога не?
2. И кой каза, че такава матрица е точно една? Ами ако за някаква оригинална матрица $A$ има цяла тълпа обратни?
3. Как изглеждат всички тези "обратни"? И как всъщност ги броите?

Що се отнася до алгоритмите за изчисление - ще говорим за това малко по-късно. Но на останалите въпроси ще отговорим точно сега. Нека ги подредим под формата на отделни твърдения-леми.

Основни свойства

Нека започнем с това как трябва да изглежда матрицата $A$, за да има $((A)^(-1))$. Сега ще се уверим, че и двете от тези матрици трябва да са квадратни и с еднакъв размер: $\left[ n\times n \right]$.

Лема 1. Дадена е матрица $A$ и нейната обратна $((A)^(-1))$. Тогава и двете от тези матрици са квадратни и имат еднакъв ред $n$.

Доказателство. Всичко е просто. Нека матрицата $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Тъй като продуктът $A\cdot ((A)^(-1))=E$ съществува по дефиниция, матриците $A$ и $((A)^(-1))$ са последователни в този ред:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( подравняване)\]

Това е пряко следствие от алгоритъма за умножение на матрици: коефициентите $n$ и $a$ са "транзитни" и трябва да бъдат равни.

В същото време обратното умножение също е дефинирано: $((A)^(-1))\cdot A=E$, така че матриците $((A)^(-1))$ и $A$ са също в съответствие в този ред:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( подравняване)\]

Така, без загуба на общост, можем да приемем, че $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Въпреки това, според дефиницията на $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, така че размерите на матриците са абсолютно еднакви:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Така се оказва, че и трите матрици - $A$, $((A)^(-1))$ и $E$ - са квадратни по размер $\left[ n\times n \right]$. Лемата е доказана.

Е, това вече е добре. Виждаме, че само квадратните матрици са обратими. Сега нека се уверим, че обратната матрица е винаги една и съща.

Лема 2. Дадена е матрица $A$ и нейната обратна $((A)^(-1))$. Тогава тази обратна матрица е уникална.

Доказателство. Да започнем от обратното: нека матрицата $A$ има поне два случая на обратни — $B$ и $C$. Тогава според определението са верни следните равенства:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \край (подравняване)\]

От лема 1 заключаваме, че и четирите матрици $A$, $B$, $C$ и $E$ са квадратни от един и същи ред: $\left[ n\times n \right]$. Следователно продуктът се определя:

Тъй като матричното умножение е асоциативно (но не комутативно!), можем да напишем:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Стрелка надясно B=C. \\ \край (подравняване)\]

Получено само възможен вариант: два екземпляра на обратната матрица са равни. Лемата е доказана.

Горното разсъждение почти дословно повтаря доказателството за уникалността на обратния елемент за всички реални числа $b\ne 0$. Единственото съществено допълнение е вземането под внимание на размерността на матриците.

Все още обаче не знаем нищо за това дали всяка квадратна матрица е обратима. Тук на помощ ни идва детерминантата – това е ключова характеристика за всички квадратни матрици.

Лема 3. Дадена е матрица $A$. Ако матрицата $((A)^(-1))$ съществува, обратна на нея, тогава детерминантата на оригиналната матрица е различна от нула:

\[\ляво| A \right|\ne 0\]

Доказателство. Вече знаем, че $A$ и $((A)^(-1))$ са квадратни матрици с размер $\left[ n\times n \right]$. Следователно за всеки от тях е възможно да се изчисли детерминантата: $\left| A \right|$ и $\left| ((A)^(-1)) \right|$. Детерминантата на продукта обаче е равна на произведението на детерминантите:

\[\ляво| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \right|\]

Но според дефиницията на $A\cdot ((A)^(-1))=E$ и детерминантата на $E$ винаги е равна на 1, така че

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E\надясно|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \край (подравняване)\]

Произведението на две числа е равно на единица само ако всяко от тези числа е различно от нула:

\[\ляво| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Така се оказва, че $\left| A \right|\ne 0$. Лемата е доказана.

Всъщност това изискване е съвсем логично. Сега ще анализираме алгоритъма за намиране на обратната матрица - и ще стане напълно ясно защо по принцип не може да съществува обратна матрица с нулев детерминант.

Но първо, нека формулираме "спомагателна" дефиниция:

Определение. Изродената матрица е квадратна матрица с размер $\left[ n\times n \right]$, чиято детерминанта е нула.

По този начин можем да твърдим, че всяка обратима матрица е неизродена.

Как да намерим обратната матрица

Сега ще разгледаме универсален алгоритъм за намиране на обратни матрици. Като цяло има два общоприети алгоритъма и днес ще разгледаме втория.

Тази, която ще разгледаме сега, е много ефективна за матрици с размер $\left[ 2\times 2 \right]$ и - отчасти - с размер $\left[ 3\times 3 \right]$. Но като се започне от размера $\left[ 4\times 4 \right]$ е по-добре да не го използвате. Защо - сега ще разберете всичко.

Алгебрични допълнения

Приготви се. Сега ще има болка. Не, не се притеснявайте: красива медицинска сестра в пола, чорапи с дантела не идва при вас и няма да ви постави инжекция в дупето. Всичко е много по-прозаично: алгебричните допълнения и Нейно Величество „Матрицата на съюза“ идват при вас.

Да започнем с основното. Нека има квадратна матрица с размер $A=\left[ n\times n \right]$, чиито елементи се наричат ​​$((a)_(ij))$. Тогава за всеки такъв елемент може да се дефинира алгебрично допълнение:

Определение. Алгебрично допълнение $((A)_(ij))$ към елемента $((a)_(ij))$ в $i$-тия ред и $j$-та колона на матрицата $A=\left [ n \times n \right]$ е конструкция на формата

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Където $M_(ij)^(*)$ е детерминантата на матрицата, получена от оригиналния $A$ чрез изтриване на същия $i$-ти ред и $j$-та колона.

Отново. Алгебричното допълнение към матричния елемент с координати $\left(i;j \right)$ се означава като $((A)_(ij))$ и се изчислява по схемата:

1. Първо изтриваме $i$-реда и $j$-тата колона от оригиналната матрица. Получаваме нова квадратна матрица и означаваме нейния детерминант като $M_(ij)^(*)$.
2. След това умножаваме този детерминант по $((\left(-1 \right))^(i+j))$ - първоначално този израз може да изглежда умопомрачителен, но всъщност просто намираме знака пред $ M_(ij)^(*) $.
3. Ние броим - получаваме конкретно число. Тези. алгебричното събиране е просто число, а не някаква нова матрица и т.н.

Самата матрица $M_(ij)^(*)$ се нарича допълнителен минор към елемента $((a)_(ij))$. И в този смисъл горната дефиниция на алгебрично допълнение е частен случай на по-сложна дефиниция - тази, която разгледахме в урока за детерминантата.

Важна забележка. Всъщност в математиката за "възрастни" алгебричните добавки се дефинират, както следва:

1. Вземаме $k$ реда и $k$ колони в квадратна матрица. При тяхното пресичане получаваме матрица с размер $\left[ k\times k \right]$ — нейният детерминант се нарича минор от порядък $k$ и се обозначава с $((M)_(k))$.
2. След това задраскваме тези "избрани" $k$ реда и $k$ колони. Отново получаваме квадратна матрица - нейният детерминант се нарича допълнителен минор и се означава с $M_(k)^(*)$.
3. Умножете $M_(k)^(*)$ по $((\left(-1 \right))^(t))$, където $t$ е (внимание!) сумата от числата на всички избрани редове и колони. Това ще бъде алгебричното добавяне.

Обърнете внимание на третата стъпка: всъщност има сума от $2k$ условия! Друго нещо е, че за $k=1$ получаваме само 2 члена - това ще бъдат същите $i+j$ - "координатите" на елемента $((a)_(ij))$, за който сме търси алгебрично допълнение.

Затова днес използваме леко опростена дефиниция. Но както ще видим по-късно, това ще бъде повече от достатъчно. Много по-важно е следното:

Определение. Обединителната матрица $S$ към квадратната матрица $A=\left[ n\times n \right]$ е нова матрица с размер $\left[ n\times n \right]$, която се получава от $A$ чрез заместване на $(( a)_(ij))$ с алгебрични допълнения $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \right]\]

Първата мисъл, която възниква в момента на осъзнаване на това определение е „ето колко трябва да броите общо!“ Спокойно: трябва да броите, но не толкова. :)

Е, всичко това е много хубаво, но защо е необходимо? Но защо.

Основна теорема

Да се ​​върнем малко назад. Спомнете си, лема 3 твърди, че една обратима матрица $A$ винаги е неособена (т.е. нейният детерминант е различен от нула: $\left| A \right|\ne 0$).

Така че обратното също е вярно: ако матрицата $A$ не е изродена, тогава тя винаги е обратима. И дори има схема за търсене $((A)^(-1))$. Виж това:

Теорема за обратната матрица. Нека е дадена квадратна матрица $A=\left[ n\times n \right]$ и нейният детерминант е различен от нула: $\left| A \right|\ne 0$. Тогава обратната матрица $((A)^(-1))$ съществува и се изчислява по формулата:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

И сега – все същото, но с четлив почерк. За да намерите обратната матрица, трябва:

1. Изчислете детерминантата $\left| A \right|$ и се уверете, че е различно от нула.
2. Компилирайте обединителната матрица $S$, т.е. пребройте 100500 алгебрични добавки $((A)_(ij))$ и ги поставете на място $((a)_(ij))$.
3. Транспонирайте тази матрица $S$ и след това я умножете по някакво число $q=(1)/(\left| A \right|)\;$.

И това е! Намерена е обратната матрица $((A)^(-1))$. Нека да разгледаме примери:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

Решение. Да проверим обратимостта. Нека изчислим детерминантата:

\[\ляво| A \дясно|=\ляво| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Детерминантата е различна от нула. Така че матрицата е обратима. Нека създадем обединителна матрица:

Нека изчислим алгебричните добавки:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\вдясно|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\вдясно|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\надясно|=3. \\ \край (подравняване)\]

Обърнете внимание: детерминанти |2|, |5|, |1| и |3| са детерминантите на матрици с размер $\left[ 1\times 1 \right]$, а не модули. Тези. ако в детерминантите имаше отрицателни числа, не е необходимо да премахвате "минуса".

Общо нашата матрица на съюза изглежда така:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (масив)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\край (масив) \right]\]

Добре, всичко свърши. Проблема решен.

Отговор. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Задача. Намерете обратната матрица:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Решение. Отново разглеждаме детерминантата:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Детерминантата е различна от нула - матрицата е обратима. Но сега ще бъде най-тенекиеното: трябва да преброите цели 9 (девет, по дяволите!) Алгебрични добавки. И всеки от тях ще съдържа квалификатора $\left[ 2\times 2 \right]$. Летя:

\[\begin(matrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\end(matrix) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\end(matrix) \right|=2; \\ \край (матрица)\]

Накратко, матрицата на обединението ще изглежда така:

Следователно обратната матрица ще бъде:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(масив) \right]\]

Е, това е всичко. Ето и отговора.

Отговор. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Както можете да видите, в края на всеки пример извършихме проверка. В тази връзка важна забележка:

Не бъдете мързеливи, за да проверите. Умножете оригиналната матрица по намерената обратна - трябва да получите $E$.

Много по-лесно и по-бързо е да извършите тази проверка, отколкото да търсите грешка в следващите изчисления, когато например решавате матрично уравнение.

Алтернативен начин

Както казах, теоремата за обратната матрица работи добре за размерите $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (във последния случай не е толкова "красиво" вече). ”), но за големите матрици започва тъгата.

Но не се притеснявайте: има алтернативен алгоритъм, който може да се използва за спокойно намиране на обратната дори за матрицата $\left[ 10\times 10 \right]$. Но, както често се случва, за да разгледаме този алгоритъм, имаме нужда от малко теоретична подготовка.

Елементарни трансформации

Сред различните трансформации на матрицата има няколко специални - те се наричат ​​елементарни. Има точно три такива трансформации:

1. Умножение. Можете да вземете $i$-тия ред (колона) и да го умножите по произволно число $k\ne 0$;
2. Допълнение. Добавете към $i$-тия ред (колона) всеки друг $j$-ти ред (колона), умножен по произволно число $k\ne 0$ (разбира се, $k=0$ също е възможно, но какъв е смисълът от това? ?Нищо няма да се промени обаче).
3. Пермутация. Вземете $i$-тия и $j$-тия ред (колони) и ги разменете.

Защо тези трансформации се наричат ​​елементарни (за големи матрици те не изглеждат толкова елементарни) и защо има само три от тях - тези въпроси са извън обхвата на днешния урок. Затова няма да навлизаме в подробности.

Друго нещо е важно: ние трябва да извършим всички тези извращения върху свързаната матрица. Да, да, чухте правилно. Сега ще има още едно определение - последното в днешния урок.

Приложена матрица

Със сигурност в училище сте решавали системи от уравнения, използвайки метода на добавяне. Е, ето, извадете друг от един ред, умножете някой ред по число - това е всичко.

И така: сега всичко ще бъде същото, но вече „по възрастен начин“. Готов?

Определение. Нека са дадени матрицата $A=\left[ n\times n \right]$ и матрицата на идентичност $E$ със същия размер $n$. Тогава свързаната матрица $\left[ A\left| E \ дясно. \right]$ е нова $\left[ n\times 2n \right]$ матрица, която изглежда така:

\[\left[ A\left| E \ дясно. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Накратко, вземаме матрицата $A$, отдясно й присвояваме матрицата за идентичност $E$ с необходимия размер, разделяме ги с вертикална лента за красота - ето я прикачената. :)

Каква е уловката? И ето какво:

Теорема. Нека матрицата $A$ е обратима. Разгледайте присъединената матрица $\left[ A\left| E \ дясно. \right]$. Ако използвате елементарни трансформациилиниипренесете го във формата $\left[ E\left| Ярък. \right]$, т.е. чрез умножаване, изваждане и пренареждане на редове, за да получите матрицата $E$ отдясно от $A$, тогава матрицата $B$, получена отляво, е обратната на $A$:

\[\left[ A\left| E \ дясно. \right]\to \left[ E\left| Ярък. \right]\Rightarrow B=((A)^(-1))\]

Толкова е просто! Накратко, алгоритъмът за намиране на обратната матрица изглежда така:

1. Напишете свързаната матрица $\left[ A\left| E \ дясно. \right]$;
2. Извършете елементарни преобразувания на низове, докато вдясно вместо $A$ се появи $E$;
3. Разбира се, нещо ще се появи и отляво - определена матрица $B$. Това ще бъде обратното;
4. ПЕЧАЛБИ! :)

Разбира се, много по-лесно е да се каже, отколкото да се направи. Нека да разгледаме няколко примера: за размерите $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.

Задача. Намерете обратната матрица:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Решение. Съставяме приложената матрица:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(масив) \right]\]

Тъй като последната колона на оригиналната матрица е пълна с единици, извадете първия ред от останалите:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(масив) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matrix)\to \\ & \to \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 \\ & 1 \\\end(array) \right] \\ \end(align)\]

Няма повече единици, с изключение на първия ред. Но ние не го докосваме, в противен случай новоотстранените единици ще започнат да се "умножават" в третата колона.

Но можем да извадим втория ред два пъти от последния - получаваме единица в долния ляв ъгъл:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(масив) \right]\begin(matrix) \ \\ \downarrow \\ -2 \\\end(matrix)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Сега можем да извадим последния ред от първия и два пъти от втория - по този начин ще "нулираме" първата колона:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \right]\begin(matrix) -1 \\ -2 \\ \стрелка нагоре \\\end(matrix)\to \\ & \ към \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Умножете втория ред по −1 и след това го извадете 6 пъти от първия и добавете 1 път към последния:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(масив) \right]\begin(matrix) -6 \\ \updownarrow \\ +1 \\\end (матрица)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(масив) \right] \\ \end(align)\]

Остава само да размените редове 1 и 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(масив) \right]\]

Готов! Вдясно е необходимата обратна матрица.

Отговор. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Задача. Намерете обратната матрица:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matrix) \right]\]

Решение. Отново съставяме прикачения:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Нека вземем малко назаем, да се погрижим колко трябва да броим сега ... и да започнем да броим. Като начало ние „нулираме“ първата колона, като извадим ред 1 от редове 2 и 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\край (масив) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Наблюдаваме твърде много "минуси" в редове 2-4. Умножете всичките три реда по −1 и след това изгорете третата колона, като извадите ред 3 от останалите:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(масив) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ляво| \cdot \left(-1 \right) \right. \\ \ляво| \cdot \left(-1 \right) \right. \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (масив) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrix)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Сега е време да "изпържим" последната колона от оригиналната матрица: извадете ред 4 от останалите:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(масив ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Последно хвърляне: "изгорете" втората колона, като извадите ред 2 от ред 1 и 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

И отново, идентичната матрица отляво, така че обратното отдясно. :)

Отговор. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrix) \right]$

Намиране на обратната матрица- проблем, който най-често се решава по два метода:

• методът на алгебричните допълнения, при който се изисква намиране на детерминанти и транспониране на матрици;
• метод на елиминиране неизвестен гаус, в който се изисква да се извършват елементарни трансформации на матрици (събиране на редове, умножаване на редове по едно и също число и т.н.).

За тези, които са особено любопитни, има и други методи, например методът на линейните трансформации. В този урок ще анализираме трите споменати метода и алгоритмите за намиране на обратната матрица чрез тези методи.

обратна матрица НО, такава матрица се нарича

НО
. (1)

обратна матрица , което се изисква да се намери за дадена квадратна матрица НО, такава матрица се нарича

продуктът, чрез който матриците НОвдясно е матрицата на идентичността, т.е.
. (1)

Идентификационната матрица е диагонална матрица, в която всички диагонални записи са равни на единица.

Теорема.За всяка неособена (неособена, неособена) квадратна матрица може да се намери обратна матрица и освен това само една. За специална (изродена, сингулярна) квадратна матрица обратната матрица не съществува.

Квадратната матрица се нарича неспециални(или неизродени, неединствен), ако неговата детерминанта не е равна на нула, и специален(или изродени, единствено число), ако неговата детерминанта е нула.

Обратната матрица може да се намери само за квадратна матрица. Естествено, обратната матрица също ще бъде квадратна и от същия ред като дадената матрица. Матрица, за която може да се намери обратна матрица, се нарича обратима матрица.

За обратна матрица има подходяща аналогия с реципрочната стойност на число. За всяко число а, което не е равно на нула, съществува число bче работата аи bравно на едно: аб= 1. Номер bсе нарича реципрочна стойност на число b. Например за числото 7 обратното е числото 1/7, тъй като 7*1/7=1.

Намиране на обратната матрица по метода на алгебричните допълнения (матрица на обединение)

За неособена квадратна матрица НОобратното е матрицата

където е матричната детерминанта НО, а е матрицата, свързана с матрицата НО.

В съюз с квадратна матрица Ае матрица от същия ред, чиито елементи са алгебричните допълнения на съответните елементи на детерминантата на матрицата, транспонирана по отношение на матрицата A. Така, ако

тогава

и

Алгоритъм за намиране на обратната матрица по метода на алгебричните събирания

1. Намерете детерминантата на тази матрица А. Ако детерминантата е равна на нула, намирането на обратната матрица спира, тъй като матрицата е изродена и за нея няма обратна.

2. Намерете матрица, транспонирана по отношение на А.

3. Изчислете елементи съюзническа матрицакато алгебрични допълнения на марица, намерени в стъпка 2.

4. Приложете формула (2): умножете реципрочната стойност на детерминантата на матрицата А, към матрицата на обединение, намерена в стъпка 4.

5. Проверете резултата, получен в стъпка 4, като умножите тази матрица Акъм обратната матрица. Ако произведението на тези матрици е равно на единичната матрица, тогава обратната матрица е намерена правилно. В противен случай стартирайте процеса на решение отново.

Пример 1За матрица

намерете обратната матрица.

Решение. За да се намери обратната матрица, е необходимо да се намери детерминантата на матрицата НО. Намираме по правилото на триъгълниците:

Следователно матрицата НОе неединично (неизродено, неединично) и има обратно за него.

Нека намерим матрицата, свързана с дадената матрица НО.

Нека намерим матрицата, транспонирана по отношение на матрицата А:

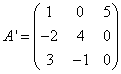
Ние изчисляваме елементите на обединителната матрица като алгебрични допълнения на матрицата, транспонирани по отношение на матрицата А:

Следователно, матрицата, конюгирана с матрицата А, има формата

Коментирайте.Редът на изчисляване на елементите и транспонирането на матрицата може да бъде различен. Първо могат да се изчислят алгебричните допълнения на матрицата А, и след това транспонирайте матрицата от алгебрични допълнения. Резултатът трябва да бъде същите елементи на обединителната матрица.

Прилагайки формула (2), намираме матрицата, обратна на матрицата НО:

Намиране на обратната матрица чрез елиминиране на неизвестните по Гаус

Първата стъпка за намиране на обратната матрица чрез елиминиране на Гаус е да се присвои на матрицата Аидентификационна матрица от същия ред, като ги разделя с вертикална черта. Получаваме двойна матрица. Умножете двете части на тази матрица по , тогава получаваме

,

Алгоритъм за намиране на обратната матрица чрез елиминиране на неизвестните по Гаус

1. Към матрицата Азадайте идентична матрица от същия ред.

2. Трансформирайте получената двойна матрица, така че матрицата за идентичност да се получи в лявата й част, след което обратната матрица автоматично ще бъде получена в дясната част на мястото на матрицата за идентичност. Матрица Аот лявата страна се преобразува в матрицата на идентичност чрез елементарни трансформации на матрицата.

2. Ако в процеса на матрична трансформация Ав матрицата за идентичност във всеки ред или във всяка колона ще има само нули, тогава детерминантата на матрицата е равна на нула и следователно матрицата Аще бъде изродена и няма обратна матрица. В този случай по-нататъшното намиране на обратната матрица спира.

Пример 2За матрица

намерете обратната матрица.

и ще го трансформираме така, че матрицата на идентичност да се получи от лявата страна. Да започнем трансформацията.

Умножете първия ред на лявата и дясната матрица по (-3) и го добавете към втория ред, след което умножете първия ред по (-4) и го добавете към третия ред, след което получаваме

.

Така че, ако е възможно, да няма дробни числа по време на следващите трансформации, първо ще създадем единица във втория ред от лявата страна на двойната матрица. За да направите това, умножете втория ред по 2 и извадете третия ред от него, тогава получаваме

.

Нека добавим първия ред към втория и след това да умножим втория ред по (-9) и да го добавим към третия ред. Тогава получаваме

.

След това разделете третия ред на 8

.

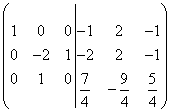Умножете третия ред по 2 и го добавете към втория ред. Оказва се:

.

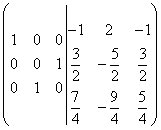Разменяйки местата на втория и третия ред, накрая получаваме:

.

Виждаме, че матрицата на идентичността се получава от лявата страна, следователно обратната матрица се получава от дясната страна. По този начин:

.

Можете да проверите правилността на изчисленията, като умножите оригиналната матрица по намерената обратна матрица:

Резултатът трябва да бъде обратна матрица.

Пример 3За матрица

намерете обратната матрица.

Решение. Съставяне на двойна матрица

и ние ще го трансформираме.

Умножаваме първия ред по 3, а втория по 2 и изваждаме от втория, след което умножаваме първия ред по 5 и третия по 2 и изваждаме от третия ред, тогава получаваме

.

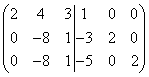Умножаваме първия ред по 2 и го добавяме към втория, след което изваждаме втория от третия ред, след което получаваме

.

Виждаме, че в третия ред от лявата страна всички елементи се оказаха равни на нула. Следователно матрицата е изродена и няма обратна матрица. Спираме по-нататъшното намиране на обратната мария.

Определение 1:Една матрица се нарича изродена, ако нейният детерминант е нула.

Определение 2:Матрицата се нарича неособена, ако нейният детерминант не е равен на нула.

Матрица "А" се нарича обратна матрица, ако е изпълнено условието A*A-1 = A-1 *A = E (матрица на идентичност).

Квадратната матрица е обратима само ако е неособена.

Схема за изчисляване на обратната матрица:

1) Изчислете детерминантата на матрицата "A", ако ∆ A = 0, тогава обратната матрица не съществува.

2) Намерете всички алгебрични допълнения на матрицата "A".

3) Съставете матрица от алгебрични добавки (Aij )

4) Транспонирайте матрицата на алгебричните допълнения (Aij )T

5) Умножете транспонираната матрица по реципрочната стойност на детерминантата на тази матрица.

6) Изпълнете проверка:

На пръв поглед може да изглежда, че е трудно, но всъщност всичко е много просто. Всички решения се основават на прости аритметични операции, основното при решаването е да не се бъркате със знаците "-" и "+" и да не ги губите.

А сега нека заедно с вас решим една практическа задача, като изчислим обратната матрица.

Задача: намерете обратната матрица "A", показана на снимката по-долу:

Решаваме всичко точно както е посочено в плана за изчисляване на обратната матрица.

1. Първото нещо, което трябва да направите, е да намерите детерминантата на матрицата "A":

Обяснение:

Опростихме нашия детерминант, като използвахме основните му функции. Първо добавихме към 2-ри и 3-ти ред елементите от първия ред, умножени по едно число.

Второ, сменихме 2-ра и 3-та колона на детерминантата и според нейните свойства сменихме знака пред нея.

Трето, извадихме общия множител (-1) на втория ред, като по този начин отново променихме знака и той стана положителен. Също така опростихме ред 3 по същия начин, както в самото начало на примера.

Имаме триъгълен детерминант, в който елементите под диагонала са равни на нула, а по свойство 7 той е равен на произведението на елементите на диагонала. В резултат на това получихме ∆ A = 26, следователно съществува обратната матрица.

A11 = 1*(3+1) = 4

A12 \u003d -1 * (9 + 2) \u003d -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Следващата стъпка е да се състави матрица от получените добавки:

5. Умножаваме тази матрица по реципрочната стойност на детерминантата, т.е. по 1/26:

6. Е, сега просто трябва да проверим:

По време на проверката получихме идентификационна матрица, следователно решението беше взето абсолютно правилно.

2 начин за изчисляване на обратната матрица.

1. Елементарно преобразуване на матрици

2. Обратна матрица чрез елементарен преобразувател.

Елементарната матрична трансформация включва:

1. Умножаване на низ с различно от нула число.

2. Добавяне към всеки ред на друг ред, умножен по число.

3. Размяна на редовете на матрицата.

4. Прилагайки верига от елементарни трансформации, получаваме друга матрица.

НО -1 = ?

1. (A|E) ~ (E|A -1 )

2. А -1*A=E

Помислете за това практически примерс реални числа.

Упражнение:Намерете обратната матрица.

Решение:

Да проверим:

Малко пояснение за решението:

Първо разменихме редове 1 и 2 на матрицата, след което умножихме първия ред по (-1).

След това първият ред беше умножен по (-2) и добавен към втория ред на матрицата. След това умножихме втория ред по 1/4.

Последният етап от трансформацията беше умножаването на втория ред по 2 и събирането от първия. В резултат на това имаме матрица за идентичност отляво, следователно обратната матрица е матрицата отдясно.

След проверка се убедихме в правилността на решението.

Както можете да видите, изчисляването на обратната матрица е много просто.

В заключение на тази лекция бих искал да отделя малко време и на свойствата на такава матрица.

Подобно на обратните в много свойства.

Енциклопедичен YouTube

1 / 5

✪ Как да намерите обратна матрица - bezbotvy

✪ Обратна матрица (2 начина за намиране)

✪ Обратна матрица №1

✪ 2015-01-28. Обратна матрица 3x3

✪ 2015-01-27. Обратна матрица 2x2

субтитри

Свойства на обратната матрица

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), където det (\displaystyle \ \det )обозначава детерминанта.
• (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1))за две квадратни обратими матрици A (\displaystyle A)и B (\displaystyle B).
• (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), където (. . .) T (\displaystyle (...)^(T))обозначава транспонираната матрица.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1))за всеки коефициент k ≠ 0 (\displaystyle k\not =0).
• E − 1 = E (\displaystyle \ E^(-1)=E).
• Ако е необходимо да се реши система от линейни уравнения , (b е ненулев вектор), където x (\displaystyle x)е желаният вектор и ако A − 1 (\displaystyle A^(-1))съществува, тогава x = A − 1 b (\displaystyle x=A^(-1)b). В противен случай или размерността на пространството на решенията е по-голяма от нула, или изобщо няма такива.

Начини за намиране на обратната матрица

Ако матрицата е обратима, тогава за да намерите обратната на матрицата, можете да използвате един от следните методи:

Точни (директни) методи

Метод на Гаус-Джордан

Нека вземем две матрици: себе си Аи единични д. Да донесем матрицата Акъм матрицата на идентичност по метода на Гаус-Джордан, прилагайки трансформации в редове (можете също да прилагате трансформации в колони, но не и в смес). След като приложите всяка операция към първата матрица, приложете същата операция към втората. Когато редуцирането на първата матрица до идентичността е завършено, втората матрица ще бъде равна на А -1.

Когато използвате метода на Гаус, първата матрица ще бъде умножена отляво по една от елементарните матрици Λ i (\displaystyle \Lambda _(i))(трансвекция или диагонална матрица с такива на главния диагонал, с изключение на една позиция):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=E \Стрелка надясно \Lambda =A^(-1)). Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 − a m − 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 − a m + 1 m / a m m 1 … 0 … 0 … 0 − a n m / a m m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\dots &0&-a_(1m)/a_(mm)&0&\dots &0\\ &&&\точки &&&\\0&\точки &1&-a_(m-1m)/a_(mm)&0&\точки &0\\0&\точки &0&1/a_(mm)&0&\точки &0\\0&\точки &0&-a_( m+1m)/a_(mm)&1&\точки &0\\&&&\точки &&&\\0&\точки &0&-a_(nm)/a_(mm)&0&\точки &1\край (bmatrix))).

Втората матрица след прилагане на всички операции ще бъде равна на Λ (\displaystyle \Lambda ), тоест ще бъде желаната. Сложността на алгоритъма - O(n 3) (\displaystyle O(n^(3))).

Използване на матрицата на алгебричните допълнения

Матрична обратна матрица A (\displaystyle A), представят във формата

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

където adj (A) (\displaystyle (\mbox(adj))(A))- прикрепена матрица;

Сложността на алгоритъма зависи от сложността на алгоритъма за изчисляване на детерминантата O det и е равна на O(n²) O det .

Използване на LU/LUP разлагане

Матрично уравнение A X = I n (\displaystyle AX=I_(n))за обратна матрица X (\displaystyle X)може да се разглежда като колекция n (\displaystyle n)системи на формата A x = b (\displaystyle Ax=b). Обозначете i (\displaystyle i)-та колона на матрицата X (\displaystyle X)през X i (\displaystyle X_(i)); тогава A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n), тъй като i (\displaystyle i)-та колона на матрицата I n (\displaystyle I_(n))е единичният вектор e i (\displaystyle e_(i)). с други думи, намирането на обратната матрица се свежда до решаване на n уравнения с една и съща матрица и различни десни части. След изпълнение на разширението на LUP (време O(n³)) всяко от n уравнения отнема O(n²) време за решаване, така че тази част от работата също отнема O(n³) време.

Ако матрицата A е неособена, тогава можем да изчислим LUP разлагането за нея PA = L U (\displaystyle PA=LU). Позволявам P A = B (\displaystyle PA=B), B − 1 = D (\displaystyle B^(-1)=D). Тогава, от свойствата на обратната матрица, можем да запишем: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Ако умножим това равенство по U и L, тогава можем да получим две равенства от формата U D = L − 1 (\displaystyle UD=L^(-1))и D L = U − 1 (\displaystyle DL=U^(-1)). Първото от тези равенства е система от n² линейни уравненияза n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2)))на които десните части са известни (от свойствата на триъгълните матрици). Втората също е система от n² линейни уравнения за n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2)))на които десните части са известни (също от свойствата на триъгълните матрици). Заедно те образуват система от n² равенства. Използвайки тези равенства, можем рекурсивно да определим всички n² елементи на матрицата D. Тогава от равенството (PA) −1 = A −1 P −1 = B −1 = D. получаваме равенството A − 1 = D P (\displaystyle A^(-1)=DP).

В случай на използване на LU декомпозиция не се изисква пермутация на колоните на матрицата D, но решението може да се разминава дори ако матрицата A е неособена.

Сложността на алгоритъма е O(n³).

Итеративни методи

Методи на Шулц

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\sum _(i=0)^(n)\Psi _(k)^(i)\end(cases)))

Оценка на грешката

Избор на начално приближение

Проблемът с избора на първоначалното приближение в разглежданите тук процеси на итеративна инверсия на матрицата не ни позволява да ги третираме като независими универсални методи, конкуриращи се с методите на директна инверсия, базирани например на LU декомпозиция на матрици. Има някои препоръки за избор U 0 (\displaystyle U_(0)), гарантиращи изпълнението на условието ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (спектралният радиус на матрицата е по-малък от единица), което е необходимо и достатъчно за конвергенцията на процеса. В този случай обаче първо се изисква да се знае отгоре оценката за спектъра на обратимата матрица A или матрицата A A T (\displaystyle AA^(T))(а именно, ако A е симетрична положително определена матрица и ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), тогава можете да вземете U 0 = α E (\displaystyle U_(0)=(\alpha )E), където ; ако A е произволна неособена матрица и ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), тогава да предположим U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), където също α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); Разбира се, ситуацията може да бъде опростена и, като се използва фактът, че ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), слагам U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). Второ, при такава спецификация на първоначалната матрица няма гаранция, че ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|)ще бъде малък (може би дори ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), и висок порядък на степен на конвергенция няма да бъде веднага очевиден.

Примери

Матрица 2х2

A − 1 = [ a b c d ] − 1 = 1 det (A) [ d − b − c a ] = 1 a d − b c [ d − b − c a ] . (\displaystyle \mathbf (A) ^(-1)=(\begin(bmatrix)a&b\\c&d\\\end(bmatrix))^(-1)=(\frac (1)(\det(\mathbf (A))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix))=(\frac (1)(ad- bc))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix)).)

Обръщането на матрица 2x2 е възможно само при условие, че a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

Методи за намиране на обратната матрица, . Помислете за квадратна матрица

Означаваме Δ = det A.

Квадратната матрица A се нарича неизроден,или неспециалниако неговата детерминанта е различна от нула, и изроден,или специален, акоΔ = 0.

Квадратна матрица B съществува за квадратна матрица A от същия ред, ако техният продукт A B = B A = E, където E е матрицата на идентичност от същия ред като матриците A и B.

Теорема . За да има матрицата A обратна матрица, е необходимо и достатъчно нейната детерминанта да е различна от нула.

Обратна матрица към матрица A, означена с A- 1, така че B = A - 1 и се изчислява по формулата

, (1)

където А i j - алгебрични добавки на елементите a i j на матрицата A..

Изчисляване A -1 по формула (1) за матрици висок редмного трудоемко, така че на практика е удобно да се намери A -1 с помощта на метода на елементарните трансформации (EP). Всяка неособена матрица A може да бъде намалена чрез EP само на колони (или само редове) към матрицата за идентичност E. Ако EP, изпълнени върху матрицата A, се прилагат в същия ред към матрицата за идентичност E, тогава резултатът е обратна матрица. Удобно е да се извърши EP върху матриците A и E едновременно, като се изпишат двете матрици една до друга през линията. Още веднъж отбелязваме, че когато търсите каноничната форма на матрица, за да я намерите, можете да използвате трансформации на редове и колони. Ако трябва да намерите обратната матрица, трябва да използвате само редове или само колони в процеса на трансформация.

Пример 2.10. За матрица намерете A -1 .

Решение.Първо намираме детерминантата на матрицата A
така че обратната матрица съществува и можем да я намерим по формулата: , където A i j (i,j=1,2,3) - алгебрични допълнения на елементи a i j от оригиналната матрица.

Където .

Пример 2.11. Използвайки метода на елементарните трансформации, намерете A -1 за матрицата: A=.

Решение.Присвояваме идентична матрица от същия ред на оригиналната матрица вдясно: . С помощта на елементарни трансформации на колони ние редуцираме лявата „половина“ до идентичността, като едновременно с това извършваме точно такива трансформации на дясната матрица.
За да направите това, разменете първата и втората колона: ~ . Добавяме първата към третата колона и първата, умножена по -2, към втората: . От първата колона изваждаме удвоената секунда, а от третата - втората, умножена по 6; . Нека добавим третата колона към първата и втората: . Умножете последната колона по -1: . Квадратната матрица, получена вдясно от вертикалната лента, е обратната матрица на дадената матрица A. И така,
.