Изчисляване на дисперсията в статистиката. Остатъчна дисперсия

За групирани данни остатъчна дисперсия- средна стойност на вътрешногруповите дисперсии:

Където σ 2 j е вътрешногруповата дисперсия на j -тата група.

За негрупирани данни остатъчна дисперсияе мярка за точността на приближението, т.е. приближаване на регресионната линия към оригиналните данни:
където y(t) е прогнозата според уравнението на тенденцията; y t – начална серия от динамика; n е броят на точките; p е броят на коефициентите на регресионното уравнение (броят на обяснителните променливи).
В този пример се нарича безпристрастна оценка на дисперсията.

Пример #1. Разпределението на работниците от три предприятия от една асоциация по тарифни категории се характеризира със следните данни:

Категория на заплатата на работника	Броят на работниците в предприятието
Категория на заплатата на работника	предприятие 1	предприятие 2	предприятие 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Определете:
1. дисперсия за всяко предприятие (вътрешногрупова дисперсия);
2. средна стойност на вътрешногруповите дисперсии;
3. междугрупова дисперсия;
4. обща дисперсия.

Решение.
Преди да се пристъпи към решаване на проблема, е необходимо да се установи коя характеристика е ефективна и коя факторна. В разглеждания пример действащият признак е "Тарифна категория", а факторният признак е "Номер (име) на предприятието".
След това имаме три групи (предприятия), за които е необходимо да се изчисли средната групова и вътрешногруповата дисперсия:

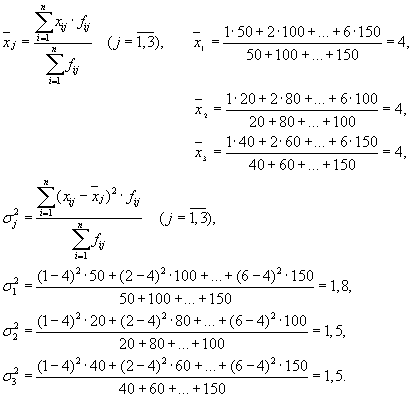
Търговско дружество	средна група,	дисперсия в рамките на групата,
1	4	1,8

Средната стойност на вътрешногруповите дисперсии ( остатъчна дисперсия), изчислено по формулата:

където можете да изчислите:

или:

тогава:
Общата дисперсия ще бъде равна на: s 2 \u003d 1,6 + 0 \u003d 1,6.
Общата дисперсия може също да се изчисли с помощта на една от следните две формули:

При решаване практически задачичесто човек трябва да работи с функция, която приема само две алтернативни стойности. В този случай те не говорят за тежестта на определена стойност на характеристика, а за нейния дял в съвкупността. Ако съотношението единици на популацията, които притежават изследваната характеристика, се означи с " Р", а не притежаване - чрез" р”, тогава дисперсията може да се изчисли по формулата:
s 2 = p×q

Пример #2. Според данните за развитието на шестима работници от бригадата, определете междугруповата вариация и оценете влиянието на работната смяна върху тяхната производителност на труда, ако общата вариация е 12,2.

No на работната бригада	Работна мощност, бр.
No на работната бригада	в първа смяна	на 2-ра смяна
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Решение. Изходни данни

х	f1	f2	е 3	f4	f5	f6	Обща сума
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Обща сума	31	33	37	37	40	38

След това имаме 6 групи, за които е необходимо да се изчисли груповата средна и вътрешногруповата дисперсия.
1. Намерете средните стойности на всяка група.

2. Намерете средния квадрат на всяка група.

Обобщаваме резултатите от изчислението в таблица:

Номер на групата	Групово средно	Вътрешногрупова дисперсия
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Вътрешногрупова дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта в рамките на групата под влияние на всички фактори, с изключение на фактора, който е в основата на групирането:
Изчисляваме средната стойност на вътрешногруповите дисперсии по формулата:

4. Междугрупова дисперсия характеризира промяната (вариацията) на изследваната (резултатна) черта под влиянието на фактор (факторна черта), лежащ в основата на групирането.
Междугруповата дисперсия се определя като:

където

Тогава

Обща дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта под въздействието на всички фактори (факторни черти) без изключение. По условието на задачата то е равно на 12,2.
емпиричен корелационна връзка измерва каква част от общата флуктуация на резултантния атрибут е причинена от изследвания фактор. Това е съотношението на факторната дисперсия към общата дисперсия:

Определяме емпиричната корелационна връзка:

Връзките между характеристиките могат да бъдат слаби или силни (близки). Техните критерии се оценяват по скалата на Chaddock:
0,1 0,3 0,5 0,7 0,9 В нашия пример връзката между функция Y фактор X е слаба
Коефициент на определяне.

Нека да определим коефициента на детерминация:

По този начин 0,67% от вариацията се дължи на разлики между признаците, а 99,37% се дължи на други фактори.
Заключение: в този случай продукцията на работниците не зависи от работата в определена смяна, т.е. влиянието на работната смяна върху тяхната производителност на труда не е значително и се дължи на други фактори.

Пример #3. Въз основа на средната стойност заплатии квадратни отклонения от неговата стойност за две групи работници, намерете общата дисперсия, като приложите правилото за добавяне на дисперсии:

Решение:
Средна стойност на дисперсиите в рамките на групата

Междугруповата дисперсия се определя като:

Общата дисперсия ще бъде: 480 + 13824 = 14304

Теорията на вероятностите е специален клон на математиката, който се изучава само от студенти от висши учебни заведения. Обичате ли изчисления и формули? Не се страхувате от перспективите за запознаване с нормалното разпределение, ансамбълната ентропия, математическото очакване и дискретната дисперсия случайна величина? Тогава тази тема ще бъде от голям интерес за вас. Нека се запознаем с някои от най-важните основни понятия на този раздел от науката.

Нека си припомним основите

Дори ако си спомняте най-простите концепции на теорията на вероятностите, не пренебрегвайте първите параграфи на статията. Факт е, че без ясно разбиране на основите, няма да можете да работите с формулите, разгледани по-долу.

И така, има някакво случайно събитие, някакъв експеримент. В резултат на извършените действия можем да получим няколко резултата – някои от тях са по-чести, други по-рядко срещани. Вероятността за събитие е съотношението на броя на действително получените резултати от един тип към общ бройвъзможен. Само знаейки класическо определениена тази концепция, можете да започнете да изучавате математическо очакванеи дисперсии на непрекъснати случайни променливи.

Средно аритметично

Още в училище, в часовете по математика, сте започнали да работите със средно аритметично. Тази концепция се използва широко в теорията на вероятностите и следователно не може да бъде пренебрегната. Основното за нас в момента е, че ще го срещнем във формулите за математическото очакване и дисперсията на случайна величина.

Имаме поредица от числа и искаме да намерим средното аритметично. Всичко, което се изисква от нас, е да сумираме всичко налично и да разделим на броя на елементите в редицата. Нека имаме числа от 1 до 9. Сумата на елементите ще бъде 45 и ще разделим тази стойност на 9. Отговор: - 5.

дисперсия

От научна гледна точка дисперсията е средният квадрат на отклоненията на получените стойности на характеристиките от средната аритметична стойност. Единият се обозначава с главна латинска буква D. Какво е необходимо за изчисляването му? За всеки елемент от редицата изчисляваме разликата между наличното число и средното аритметично и го повдигаме на квадрат. Ще има точно толкова стойности, колкото могат да бъдат резултатите за събитието, което обмисляме. След това обобщаваме всичко получено и разделяме на броя на елементите в последователността. Ако имаме пет възможни резултата, тогава разделете на пет.

Дисперсията също има свойства, които трябва да запомните, за да я приложите при решаване на задачи. Например, ако случайната променлива се увеличи с X пъти, дисперсията се увеличава с X пъти квадрата (т.е. X*X). Той никога не е по-малък от нула и не зависи от изместване на стойности с еднаква стойност нагоре или надолу. Освен това за независими тестоведисперсията на сумата е равна на сумата от дисперсиите.

Сега определено трябва да разгледаме примери за дисперсията на дискретна случайна променлива и математическото очакване.

Да кажем, че провеждаме 21 експеримента и получаваме 7 различни резултата. Наблюдавахме всеки от тях съответно 1,2,2,3,4,4 и 5 пъти. Каква ще бъде дисперсията?

Първо изчисляваме средното аритметично: сборът на елементите, разбира се, е 21. Разделяме го на 7, получавайки 3. Сега изваждаме 3 от всяко число в оригиналната последователност, поставяме на квадрат всяка стойност и събираме резултатите заедно . Оказва се 12. Сега остава да разделим числото на броя на елементите и, изглежда, това е всичко. Но има една уловка! Нека го обсъдим.

Зависимост от броя на експериментите

Оказва се, че при изчисляване на дисперсията знаменателят може да бъде едно от две числа: N или N-1. Тук N е броят на извършените експерименти или броят на елементите в последователността (което по същество е едно и също нещо). От какво зависи?

Ако броят на тестовете се измерва в стотици, тогава в знаменателя трябва да поставим N. Ако в единици, тогава N-1. Учените решиха да начертаят границата съвсем символично: днес тя минава по числото 30. Ако сме провели по-малко от 30 експеримента, тогава ще разделим количеството на N-1, а ако е повече, тогава на N.

Задача

Нека се върнем към нашия пример за решаване на проблема с дисперсията и очакването. Имаме междинно число 12, което трябваше да бъде разделено на N или N-1. Тъй като проведохме 21 експеримента, което е по-малко от 30, ще изберем втория вариант. Така че отговорът е: дисперсията е 12/2 = 2.

Очаквана стойност

Нека да преминем към втората концепция, която трябва да разгледаме в тази статия. Математическото очакване е резултат от събиране на всички възможни резултати, умножени по съответните вероятности. Важно е да се разбере, че получената стойност, както и резултатът от изчисляването на дисперсията, се получават само веднъж за цялата задача, без значение колко резултата разглежда.

Формулата за математическо очакване е доста проста: вземаме резултата, умножаваме го по неговата вероятност, добавяме същото за втория, третия резултат и т.н. Всичко, свързано с тази концепция, е лесно за изчисляване. Например сумата от математическите очаквания е равна на математическото очакване на сумата. Същото важи и за работата. Не всяка величина в теорията на вероятностите позволява извършването на такива прости операции. Нека вземем една задача и изчислим стойността на две понятия, които сме изучавали едновременно. Освен това бяхме разсеяни от теория - време е за практика.

Още един пример

Проведохме 50 опита и получихме 10 вида резултати - числа от 0 до 9 - появяващи се в различни проценти. Това са съответно: 2%, 10%, 4%, 14%, 2%, 18%, 6%, 16%, 10%, 18%. Припомнете си, че за да получите вероятностите, трябва да разделите процентните стойности на 100. Така получаваме 0,02; 0,1 и т.н. Нека представим пример за решаване на задачата за дисперсията на случайна променлива и математическото очакване.

Изчисляваме средното аритметично по формулата, която помним от началното училище: 50/10 = 5.

Сега нека преведем вероятностите в броя на резултатите "на парчета", за да направим по-удобно броенето. Получаваме 1, 5, 2, 7, 1, 9, 3, 8, 5 и 9. От всяка получена стойност изваждаме средноаритметичното, след което всеки от получените резултати повдигаме на квадрат. Вижте как да направите това с първия елемент като пример: 1 - 5 = (-4). Освен това: (-4) * (-4) = 16. За други стойности направете тези операции сами. Ако сте направили всичко правилно, след като добавите всичко, получавате 90.

Нека продължим да изчисляваме дисперсията и средната стойност, като разделим 90 на N. Защо избираме N, а не N-1? Точно така, защото броят на извършените експерименти надхвърля 30. И така: 90/10 = 9. Получихме дисперсията. Ако получите различен номер, не се отчайвайте. Най-вероятно сте направили банална грешка в изчисленията. Проверете отново какво сте написали и със сигурност всичко ще си дойде на мястото.

И накрая, нека си припомним формулата за математическо очакване. Няма да даваме всички изчисления, а само ще напишем отговора, с който можете да проверите, след като изпълните всички необходими процедури. Очакваната стойност ще бъде 5,48. Припомняме само как да извършваме операции, като използваме примера на първите елементи: 0 * 0,02 + 1 * 0,1 ... и така нататък. Както можете да видите, ние просто умножаваме стойността на резултата по неговата вероятност.

отклонение

Друга концепция, тясно свързана с дисперсията и математическото очакване, е стандартното отклонение. Отбелязва се или с латински букви sd или гръцка малка буква "сигма". Тази концепция показва как средно стойностите се отклоняват от централната характеристика. За да намерите стойността му, трябва да изчислите Корен квадратенот дисперсия.

Ако направите графика нормална дистрибуцияи искате да видите квадратното отклонение директно върху него, това може да стане в няколко стъпки. Вземете половината от изображението отляво или отдясно на режима (централна стойност), начертайте перпендикуляр на хоризонталната ос, така че площите на получените фигури да са равни. Стойността на сегмента между средата на разпределението и получената проекция върху хоризонталната ос ще бъде стандартното отклонение.

Софтуер

Както се вижда от описанията на формулите и представените примери, изчисляването на дисперсията и математическото очакване не е най-лесната процедура от аритметична гледна точка. За да не губите време, има смисъл да използвате програмата, използвана в по-високите образователни институции- нарича се "R". Той има функции, които ви позволяват да изчислявате стойности за много понятия от статистиката и теорията на вероятностите.

Например дефинирате вектор от стойности. Това става по следния начин: вектор<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.

Накрая

Дисперсията и математическото очакване са тези, без които е трудно да се изчисли нещо в бъдещето. В основния курс на лекциите в университетите те се разглеждат още в първите месеци на изучаване на предмета. Именно поради неразбирането на тези прости понятия и невъзможността да ги изчислят, много студенти веднага започват да изостават в програмата и по-късно получават слаби оценки в края на сесията, което ги лишава от стипендии.

Практикувайте поне една седмица по половин час на ден, като решавате задачи, подобни на представените в тази статия. След това, на всеки тест по теория на вероятностите, ще се справите с примери без странични съвети и измамни листове.

Дисперсията е мярка за дисперсия, която описва относителното отклонение между стойностите на данните и средната стойност. Това е най-често използваната мярка за дисперсия в статистиката, изчислена чрез сумиране на квадрат на отклонението на всяка стойност на данните от средната стойност. Формулата за изчисляване на дисперсията е показана по-долу:

s 2 - дисперсия на извадката;

x cf е средната стойност на извадката;

н — размер на извадката (брой стойности на данните),

(x i – x cf) е отклонението от средната стойност за всяка стойност от набора от данни.

За да разберем по-добре формулата, нека разгледаме един пример. Не обичам много да готвя, така че рядко го правя. Все пак, за да не умра от глад, от време на време трябва да отида до печката, за да изпълня плана за насищане на тялото си с протеини, мазнини и въглехидрати. Наборът от данни по-долу показва колко пъти Ренат готви храна всеки месец:

Първата стъпка при изчисляването на дисперсията е да се определи средната стойност на извадката, която в нашия пример е 7,8 пъти на месец. Останалите изчисления могат да бъдат улеснени с помощта на следната таблица.

Последната фаза на изчисляване на дисперсията изглежда така:

За тези, които обичат да правят всички изчисления наведнъж, уравнението ще изглежда така:

Използване на метода за броене на суровини (пример за готвене)

Има по-ефективен начин за изчисляване на дисперсията, известен като метод на "сурово броене". Въпреки че на пръв поглед уравнението може да изглежда доста тромаво, всъщност не е толкова страшно. Можете да проверите това и след това да решите кой метод ви харесва най-добре.

е сумата от всяка стойност на данните след повдигане на квадрат,

е квадратът на сумата от всички стойности на данните.

Не си губете ума точно сега. Нека поставим всичко под формата на таблица и тогава ще видите, че тук има по-малко изчисления, отколкото в предишния пример.

Както можете да видите, резултатът е същият като при използване на предишния метод. Предимствата на този метод стават очевидни с нарастването на размера на извадката (n).

Изчисляване на дисперсия в Excel

Както вероятно вече се досещате, Excel има формула, която ви позволява да изчислите дисперсията. Освен това, като се започне от Excel 2010, можете да намерите 4 разновидности на дисперсионната формула:

1) VAR.V – Връща дисперсията на извадката. Булевите стойности и текстът се игнорират.

2) VAR.G – Връща дисперсията на популацията. Булевите стойности и текстът се игнорират.

3) VASP – Връща примерната вариация, като взема предвид булевите и текстовите стойности.

4) VARP – Връща дисперсията на съвкупността, като взема предвид логическите и текстовите стойности.

Първо, нека да разгледаме разликата между извадка и популация. Целта на описателната статистика е да обобщава или показва данни по такъв начин, че бързо да се получи голяма картина, така да се каже, преглед. Статистическото заключение ви позволява да правите изводи за популация въз основа на извадка от данни от тази популация. Популацията представлява всички възможни резултати или измервания, които са от интерес за нас. Извадката е подмножество от популация.

Например, интересуваме се от сбора на група студенти от един от руските университети и трябва да определим средния резултат на групата. Можем да изчислим средното представяне на учениците и тогава получената цифра ще бъде параметър, тъй като цялото население ще бъде включено в нашите изчисления. Ако обаче искаме да изчислим GPA на всички ученици у нас, тогава тази група ще бъде нашата извадка.

Разликата във формулата за изчисляване на дисперсията между извадката и съвкупността е в знаменателя. Където за извадката ще бъде равно на (n-1), а за генералната съвкупност само n.

Сега нека се заемем с функциите за изчисляване на дисперсията с окончания НО,в описанието на което се казва, че изчислението взема предвид текстови и логически стойности. В този случай, когато се изчислява дисперсията на конкретен набор от данни, където се срещат нечислови стойности, Excel ще интерпретира текста и фалшивите булеви стойности като 0, а истинските булеви стойности като 1.

Така че, ако имате масив от данни, няма да е трудно да изчислите дисперсията му с помощта на една от изброените по-горе функции на Excel.

дисперсия (разсейване) на случайна променлива е математическото очакване на квадрата на отклонението на случайна променлива от нейното математическо очакване:

За да изчислите дисперсията, можете да използвате леко модифицирана формула

защото M(X), 2 и
са постоянни стойности. По този начин,

4.2.2. Свойства на дисперсия

Имот 1.Дисперсията на постоянна стойност е нула. Наистина, по дефиниция

Имот 2.Константният фактор може да бъде изваден от знака на дисперсията чрез повдигането му на квадрат.

Доказателство

Центрирано случайна променлива е отклонението на случайна променлива от нейното математическо очакване:

Центрираната стойност има две свойства, които са удобни за трансформация:

Имот 3.Ако случайните променливи X и Yнезависим, тогава

Доказателство. Обозначете
. Тогава.

Във втория член, поради независимостта на случайните променливи и свойствата на центрираните случайни променливи

Пример 4.5.Ако аи bса постоянни, тогава D (аX+b)= д(аX)+д(b)=
.

4.2.3. Стандартно отклонение

Дисперсията, като характеристика на разпространението на случайна променлива, има един недостатък. ако напр. х– грешката на измерване има размерност ММ, тогава дисперсията има размерността
. Поради това често се предпочита да се използва друга характеристика на разсейване - стандартно отклонение , което е равно на корен квадратен от дисперсията

Стандартното отклонение има същото измерение като самата случайна променлива.

Пример 4.6.Вариация на броя на поява на събитие в схемата на независими опити

Произведено ннезависими опити и вероятността за възникване на събитие във всеки опит е Р. Изразяваме, както и преди, броя на настъпване на събитието хчрез броя на появата на събитието в отделните експерименти:

Тъй като експериментите са независими, случайните променливи, свързани с експериментите независима. И то по силата на независимост ние имаме

Но всяка от случайните променливи има закон на разпределение (пример 3.2)

и
(пример 4.4). Следователно, по дефиниция на дисперсия:

където р=1- стр.

В резултат на това имаме
,

Стандартното отклонение на броя на случванията на събитие в ннезависими експерименти
.

4.3. Моменти на случайни променливи

В допълнение към вече разгледаните, случайните променливи имат много други числени характеристики.

Начален момент к х (
) се нарича математическо очакване кта степен на тази случайна променлива.

Централна точка кслучайна променлива от -ти ред хсе нарича очакване кта степен на съответната центрирана величина.

Лесно се вижда, че централният момент от първи ред винаги е равен на нула, централният момент от втори ред е равен на дисперсията, тъй като .

Централният момент от третия ред дава представа за асиметрията на разпределението на случайна променлива. Моментите на ред, по-висок от втория, се използват сравнително рядко, така че ще се ограничим само до понятията за тях.

4.4. Примери за намиране на закони за разпределение

Разгледайте примери за намиране на законите за разпределение на случайни променливи и техните числени характеристики.

Пример 4.7.

Съставете закона за разпределение на броя на попаденията в мишената с три изстрела в мишената, ако вероятността за попадение с всеки изстрел е 0,4. Намерете интегрална функция Е(Х)за полученото разпределение на дискретна случайна променлива хи начертайте неговата графика. Намерете математическото очакване М(х) , дисперсия д(х) и стандартно отклонение
(х) случайна величина х.

Решение

1) Дискретна случайна променлива х- броят на попаденията в целта с три изстрела - може да приеме четири стойности: 0, 1, 2, 3 . Вероятността тя да приеме всеки от тях намираме по формулата на Бернули за: н=3,стр=0,4,р=1- стр=0,6 и м=0, 1, 2, 3:

Получете вероятностите на възможните стойности х:;

Нека съставим желания закон за разпределение на случайна променлива х:

Контрола: 0,216+0,432+0,288+0,064=1.

Нека изградим полигон на разпределение на получената случайна променлива х. За да направите това, в правоъгълна координатна система маркирайте точките (0; 0.216), (1; 0.432), (2; 0.288), (3; 0.064). Нека свържем тези точки с отсечки, получената прекъсната линия е желаният многоъгълник на разпределение (фиг. 4.1).

2) Ако x 0, тогава Е(Х)=0. Наистина, за стойности, по-малки от нула, стойността хне приема. Следователно, за всички х0 , използвайки определението Е(Х), получаваме Е(Х)=П(х< х) =0 (като вероятност за невъзможно събитие).

Ако 0 , тогава Е(х) =0,216. Наистина, в този случай Е(Х)=П(х< х) = =П(- < х 0)+ П(0< х< х) =0,216+0=0,216.

Ако вземем напр. х=0,2, тогава Е(0,2)=П(х<0,2) . Но вероятността от събитие х<0,2 равна 0,216, так как случайная величинахсамо в един случай приема стойност по-малка от 0,2, а именно 0 с вероятност 0,216.

Ако 1 , тогава

Наистина ли, хможе да приеме стойност 0 с вероятност 0,216 и стойност 1 с вероятност 0,432; следователно една от тези стойности, без значение коя, хможе да приеме (според теоремата за събиране на вероятности от несъвместими събития) с вероятност от 0,648.

Ако 2 , тогава, аргументирайки се по подобен начин, получаваме Е(Х)=0,216+0,432 + + 0,288=0,936. Наистина, нека напр. х=3. Тогава Е(3)=П(х<3) изразява вероятността от събитие х<3 – стрелок сделает меньше трех попаданий, т.е. ноль, один или два. Применяя теорему сложения вероятностей, получим указанное значение функцииЕ(Х).

Ако х>3 тогава Е(Х)=0,216+0,432+0,288+0,064=1. Действително събитието х
е надежден и неговата вероятност е равна на единица, и х>3 - невъзможно. Като се има предвид това

Е(Х)=П(х< х) =П(х 3) + П(3< х< х) , получаваме посочения резултат.

Така се получава желаната интегрална функция на разпределение на случайната променлива X:

Е(х) =

чиято графика е показана на фиг. 4.2.

3) Математическото очакване на дискретна случайна променлива е равно на сумата от продуктите на всички възможни стойности хна техните вероятности:

M(X)=0=1,2.

Тоест средно има едно попадение в целта с три изстрела.

Дисперсията може да се изчисли от определението за дисперсия д(х)= М(х- М(х)) или използвайте формулата д(х)= М(х
, което води до целта по-бързо.

Нека напишем закона за разпределение на случайна променлива х :

Намерете математическото очакване за х:

M(X ) = 04
= 2,16.

Нека изчислим желаната дисперсия:

д(х) = М(х ) – (М(х)) = 2,16 – (1,2)= 0,72.

Средното квадратично отклонение се намира по формулата

(х) =
= 0,848.

Интервал ( М- ; М+ ) = (1.2-0.85; 1.2+0.85) = (0.35; 2.05) - интервалът на най-вероятните стойности на случайната променлива х, стойностите 1 и 2 попадат в него.

Пример 4.8.

Дадена е диференциалната функция на разпределение (функция на плътност) на непрекъсната случайна променлива х:

f(х) =

1) Дефинирайте постоянен параметър а.

2) Намерете интегралната функция Е(х) .

3) Начертайте графики на функции f(х) и Е(х) .

4) Намерете два начина на вероятности P(0,5< х 1,5) и П(1,5< х<3,5) .

5). Намерете математическото очакване M(X), дисперсия д(Х)и стандартно отклонение
случайна величина х.

Решение

1) Диференциална функция по свойство f(х) трябва да отговаря на условието
.

Нека изчислим този неправилен интеграл за дадената функция f(х) :

Като заместим този резултат в лявата страна на равенството, получаваме това а=1. В условието за f(х) променете параметъра ана 1:

2) Да намериш Е(х) използвайте формулата

Ако x
, тогава
, следователно,

Ако 1
тогава

Ако x>2 тогава

И така, желаната интегрална функция Е(х) изглежда като:

3) Да построим графики на функции f(х) и Е(х) (фиг. 4.3 и 4.4).

4) Вероятността за попадение на случайна променлива в даден интервал (а,b) изчислено по формулата
, ако функцията е известна f(х), и според формулата П(а < х < b) = Е(b) – Е(а), ако функцията е известна Е(х).

Да намерим
като използвате две формули и сравнете резултатите. По условие а=0,5;b=1,5; функция f(х) посочени в параграф 1). Следователно желаната вероятност според формулата е:

Същата вероятност може да се изчисли по формула b) чрез увеличението, получено в параграф 2). интегрална функция Е(х) на този интервал:

защото Е(0,5)=0.

По същия начин намираме

защото Е(3,5)=1.

5) Да се намери математическото очакване M(X)използвайте формулата
функция f(х) дадено в решението на параграф 1), то е равно на нула извън интервала (1,2]: