Прилагане на първата забележителна граница. Първа забележителна граница: теория и примери

Намерете прекрасни границитрудно е не само за много студенти от първа, втора година на обучение, които изучават теорията на границите, но и за някои учители.

Формула на първата забележителна граница

Последици от първото забележително ограничение напишете формулите
1. 2. 3. 4. Но сами по себе си общите формули на забележителни граници не помагат на никого на изпит или тест. Изводът е, че реалните задачи са построени така, че формулите, написани по-горе, все още трябва да бъдат достигнати. И повечето от студентите, които пропускат часове, изучават този курс задочно или имат учители, които сами не винаги разбират какво обясняват, не могат да изчислят най-елементарните примери до забележителни граници. От формулите на първата забележителна граница виждаме, че те могат да се използват за изследване на несигурности като нула, разделена на нула за изрази с тригонометрични функции. Разгледайте първо няколко примера за първия прекрасен лимит y и след това ще проучим втората забележителна граница.

Пример 1. Намерете границата на функцията sin(7*x)/(5*x)
Решение: Както можете да видите, функцията под границата е близо до първата забележителна граница, но границата на самата функция определено не е равна на единица. При такива присвоявания на границите трябва да се отдели в знаменателя променлива със същия коефициент, който се съдържа в променливата под синуса. В този случай разделете и умножете по 7

За някои подобно уточняване ще изглежда излишно, но за повечето ученици, на които им е трудно да дадат ограничения, това ще помогне да разберат по-добре правилата и да научат теоретичния материал.
Освен това, ако има обратен изгледфункции е и първото забележително ограничение. И всичко това, защото чудесната граница е равна на едно

Същото правило важи и за последствията от 1 забележителен лимит. Ето защо, ако ви попитат "Коя е първата прекрасна граница?" Трябва да отговорите без колебание, че е единица.

Пример 2. Намерете границата на функцията sin(6x)/tan(11x)
Решение: За да разберем крайния резултат, записваме функцията във формата

За да приложите правилата на забележителната граница, умножете и разделете на множители

След това записваме границата на произведението на функциите по отношение на произведението на границите

Без сложни формули намерихме границата на няколко тригонометрични функции. За асимилация прости формулиопитайте се да измислите и намерите границата на 2 и 4, формулата на следствие 1 от чудесната граница. Ще разгледаме по-сложни задачи.

Пример 3. Изчислете лимит (1-cos(x))/x^2
Решение: При проверка чрез заместване получаваме неопределеността 0/0 . Мнозина не знаят как да сведат такъв пример до 1 прекрасна граница. Тук трябва да използвате тригонометричната формула

В този случай лимитът ще бъде преобразуван в ясна форма

Успяхме да сведем функцията до квадрат на забележителна граница.

Пример 4. Намерете границата
Решение: При заместване получаваме познатата характеристика 0/0. Въпреки това, променливата се доближава до Pi, а не до нула. Следователно, за да приложим първото забележително ограничение, ще извършим такава промяна в променливата x, така че новата променлива да отиде на нула. За да направим това, означаваме знаменателя като новата променлива Pi-x=y

Така с помощта на тригонометричната формула, която е дадена в предходната задача, примерът се свежда до 1 прекрасна граница.

Пример 5 Изчисляване на лимит
Решение: Първоначално не е ясно как да се опростят ограниченията. Но щом има пример, значи трябва да има и отговор. Фактът, че променливата отива към единица, дава, при заместване, сингулярност на формата нула, умножена по безкрайност, така че допирателната трябва да бъде заменена с формулата

След това получаваме желаната несигурност 0/0. След това извършваме промяна на променливите в границата и използваме периодичността на котангенса

Последните замествания ни позволяват да използваме следствие 1 от забележителната граница.

Втората забележителна граница е равна на показателя

Това е класика, на която при реални проблеми не винаги е лесно да се достигнат границите.
За изчисления ще ви трябва ограниченията са следствие от второто забележително ограничение:
1. 2. 3. 4.
Благодарение на второто забележително ограничение и неговите последствия, човек може да изследва несигурности като нула, разделена на нула, единица на степен безкрайност и безкрайност, разделена на безкрайност, и дори до същата степен.

Нека започнем с няколко прости примера.

Пример 6 Намерете границата на функция
Решение: Директното прилагане на 2 чудесни лимита няма да работи. Първо трябва да завъртите индикатора така, че да има формата, обратна на члена в скоби

Това е техниката на редукция до забележителната граница 2 и всъщност извеждането на формулата 2 на следствието от границата.

Пример 7 Намерете границата на функция
Решение: Имаме задачи за формулата 3 на следствие 2 от забележителната граница. Нулевото заместване дава сингулярност под формата 0/0. За да увеличим границата по правилото, обръщаме знаменателя така, че променливата да има същия коефициент като в логаритъма

Освен това е лесно за разбиране и изпълнение на изпита. Трудностите на учениците при изчисляване на границите започват със следните задачи.

Пример 8 Изчислете границата на функцията[(x+7)/(x-3)]^(x-2)
Решение: Имаме сингулярност от тип 1 на степен безкрайност. Ако не ми вярвате, можете да замените безкрайността вместо „x“ навсякъде и да се убедите сами. За да повдигнем по правилото, разделяме числителя на знаменателя в скоби, за това първо извършваме манипулациите

Заместете израза в лимита и го завъртете до 2 чудесен лимит

Границата е степента на степен 10. Константите, които са термини с променлива както в скоби, така и в степен, не допринасят за никакво "време" - това трябва да се помни. И ако учителите ви попитат - "Защо не завъртите индикатора?" (За този пример в x-3), тогава кажете, че „Когато една променлива клони към безкрайност, добавете 100 към нея или извадете 1000 и границата ще остане същата!“.
Има втори начин за изчисляване на лимити от този тип. Ще говорим за това в следващата задача.

Пример 9 Намерете границата
Решение: Сега изваждаме променливата в числителя и знаменателя и превръщаме една характеристика в друга. За да получим крайната стойност, използваме формулата от следствие 2 на забележителната граница

Пример 10 Намерете границата на функция
Решение: Не всеки може да намери дадения лимит. За да увеличите границата до 2, представете си, че sin (3x) е променлива и трябва да обърнете експонентата

След това записваме индикатора като степен в степен


Междинните аргументи са описани в скоби. В резултат на използването на първата и втората чудесна граница, получихме степента в куб.

Пример 11. Изчислете границата на функцията sin(2*x)/log(3*x+1)
Решение: Имаме несигурност от формата 0/0. Освен това виждаме, че функцията трябва да се преобразува в използването на двете прекрасни граници. Нека извършим предишните математически трансформации

Освен това, без затруднения, границата приема стойността

Ето как ще се чувствате спокойни на тестове, тестове, модули, ако се научите как бързо да рисувате функции и да ги свеждате до първата или втората прекрасна граница. Ако ви е трудно да запомните горните методи за намиране на граници, винаги можете да поръчате тестдо нашите граници.
За да направите това, попълнете формуляра, посочете данните и прикачете файл с примери. Помогнахме на много студенти - можем да помогнем и на вас!

Първата забележителна граница често се използва за изчисляване на граници, съдържащи синус, аркуссинус, тангенс, арктангенс и произтичащите несигурности нула, разделена на нула.

Формула

Формулата за първата забележителна граница е: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$

Забелязваме, че $ \alpha\to 0 $ дава $ \sin\alpha \to 0 $, следователно имаме нули в числителя и знаменателя. Следователно, формулата на първата забележителна граница е необходима, за да разкрие несигурността на $ \frac(0)(0) $.

За да се приложи формулата, трябва да бъдат изпълнени две условия:

1. Изразите, съдържащи се в синуса и знаменателя на дробта, са еднакви
2. Изразите в синуса и знаменателя на дроб клонят към нула

внимание! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Въпреки че изразите под синуса и в знаменателя са еднакви, обаче $ 2x ^2+1 = 1 $, когато $ x\to 0 $. Второто условие не е изпълнено, поради което формулата НЕ МОЖЕ да се приложи!

Последствия

Доста рядко в задачите можете да видите чиста първа прекрасна граница, в която веднага можете да запишете отговора. На практика всичко изглежда малко по-сложно, но за такива случаи ще бъде полезно да знаете последствията от първото забележително ограничение. Благодарение на тях можете бързо да изчислите желаните граници.

$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$

$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$

Примери за решения

Нека разгледаме първата забележителна граница, примери за чието решение за изчисляване на граници, съдържащи тригонометрични функции и несигурност $ \bigg[\frac(0)(0)\bigg] $

Пример 1

Изчислете $ \lim_(x\to 0) \frac(\sin2x)(4x) $

Решение

Помислете за границата и отбележете, че тя съдържа синус. След това заместваме $ x = 0 $ в числителя и знаменателя и получаваме несигурността на нула, разделена на нула: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)( 0) $$ Вече има два знака, че трябва да приложите чудесна граница, но има малък нюанс: няма да можем веднага да приложим формулата, тъй като изразът под знака синус се различава от израза в знаменателя. И имаме нужда те да бъдат равни. Затова с помощта елементарни трансформациичислител го превръщаме в $2x$. За да направим това, ще извадим двойката от знаменателя на дробта с отделен фактор. Изглежда така: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ , че в края $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ се получава по формулата. Ако не можете да разрешите проблема си, изпратете го до нас. Ние ще осигурим подробно решение. Ще можете да се запознаете с хода на изчислението и да съберете информация. Това ще ви помогне да получите кредит от учителя своевременно!

Отговор

$$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$

Пример 2

Намерете $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $

Решение

Както винаги, първо трябва да знаете вида на несигурността. Ако е нула, разделена на нула, тогава обръщаме внимание на наличието на синус: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Тази несигурност ни позволява да използваме формулата на първата забележителна граница, но изразът от знаменателя не е равен на аргумента на синуса? Следователно е невъзможно да се приложи формулата "на челото". Трябва да умножите и разделите дробта на аргумента синус: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x-x^ 4)(x ^3+2x)) = $$ Сега описваме свойствата на границите: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x-x^4 )\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ Второто ограничение просто пасва на формулата и е равно на едно: $ $ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x)(2x- x^4) = $$ Заместете отново $ x = 0 $ в дроб и получете несигурността $ \frac(0)(0) $. За да го премахнете, достатъчно е да извадите $ x $ извън скобите и да намалите с него: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$

Отговор

$$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$

Пример 4

Изчислете $ \lim_(x\to0) \frac(\sin2x)(tg3x) $

Решение

Нека започнем изчислението, като заместим $ x=0 $. В резултат на това получаваме несигурността $ \frac(0)(0) $. Границата съдържа синус и тангенс, което подсказва за възможно развитие на ситуацията, използвайки формулата на първата забележителна граница. Нека трансформираме числителя и знаменателя на дробта във формула и следствие: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Сега виждаме, че в числителя и знаменателя има изрази, подходящи за формулата и последствията. Аргументът на синуса и аргумента на тангенса са еднакви за съответните знаменатели $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$

Отговор

$$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$

В статията: „Първата забележителна граница, примери за решения“ беше разказано за случаите, в които е препоръчително да се използва тази формула и нейните последствия.

От горната статия можете да разберете каква е границата и с какво се яде - това е МНОГО важно. Защо? Може да не разбирате какви са детерминантите и да ги решавате успешно, може изобщо да не разбирате какво е производна и да ги намирате на "петицата". Но ако не разбирате какво е лимит, тогава ще бъде трудно да решите практически задачи. Също така няма да е излишно да се запознаете с образците на дизайна на решенията и моите препоръки за дизайн. Цялата информация е представена по прост и достъпен начин.

А за целите на този урок са ни необходими следните методически материали: Забележителни границии Тригонометрични формули. Те могат да бъдат намерени на страницата. Най-добре е да отпечатате ръководствата - това е много по-удобно, освен това те често трябва да бъдат достъпни офлайн.

Какво е забележителното в прекрасните граници? Забележителността на тези граници се крие във факта, че те са доказани от най-големите умове на известни математици и благодарните потомци не трябва да страдат от ужасни граници с купчина тригонометрични функции, логаритми и степени. Тоест при намирането на границите ще използваме готови резултати, които са доказани теоретично.

Има няколко забележителни ограничения, но на практика задочниците в 95% от случаите имат две забележителни ограничения: Първият прекрасен лимит, Втората прекрасна граница. Трябва да се отбележи, че това са исторически установени имена и когато например говорят за „първата забележителна граница“, те имат предвид под това много специфично нещо, а не някаква произволна граница, взета от тавана.

Първият прекрасен лимит

Помислете за следното ограничение: (вместо родната буква „той“ ще използвам гръцка буква"алфа", той е по-удобен по отношение на представянето на материала).

Според нашето правило за намиране на граници (вижте статията Ограничения. Примери за решения) се опитваме да заместим нула във функцията: в числителя получаваме нула (синусът на нулата е нула), в знаменателя, очевидно, също нула. Така се сблъскваме с неопределеност на формата, която, за щастие, не е необходимо да се разкрива. Знам математически анализ, се доказва, че:

Този математически факт се нарича Първият прекрасен лимит. Няма да давам аналитично доказателство за лимита, но ето го геометричен смисълНека да разгледаме урока безкрайно малки функции.

Често в практическите задачи функциите могат да бъдат подредени по различен начин, това не променя нищо:

– същата първа прекрасна граница.

Но не можете сами да пренаредите числителя и знаменателя! Ако границата е дадена във формата, тогава тя трябва да бъде решена в същата форма, без да се пренарежда нищо.

На практика не само променлива може да действа като параметър, но и елементарна функция, сложна функция. Важно е само да клони към нула.

Примери:
, , ,

Тук , , , , и всичко бръмчи - приложимо е първото прекрасно ограничение.

И ето следващият запис - ерес:

Защо? Тъй като полиномът не клони към нула, той клони към пет.

Между другото въпросът е за насипване, но каква е границата ? Отговорът може да бъде намерен в края на урока.

На практика не всичко е толкова гладко, почти никога на ученик няма да бъде предложено да реши безплатен лимит и да получи лесен кредит. Хммм... Пиша тези редове и ми хрумна една много важна мисъл - все пак май е по-добре да помним наизуст "свободните" математически дефиниции и формули, това може да бъде от безценна помощ в теста, когато въпросът ще бъде решен между „две“ и „три“ и учителят решава да зададе на ученика някакъв прост въпрос или предложение за решаване най-простият пример(„може би той (а) все още знае какво ?!“).

Да преминем към разглеждането практически примери:

Пример 1

Намерете границата

Ако забележим синус в границата, това веднага трябва да ни накара да мислим за възможността за прилагане на първата забележителна граница.

Първо се опитваме да заменим 0 в израза под знака за граница (правим това мислено или на чернова):

И така, имаме неопределеност на формата, нейната не забравяйте да посочитепри вземане на решение. Изразът под знака за граница изглежда като първата прекрасна граница, но това не е съвсем, това е под синуса, но в знаменателя.

В такива случаи трябва сами да организираме първия прекрасен лимит, използвайки изкуствено устройство. Линията на разсъждение може да бъде следната: „под синуса имаме, което означава, че трябва да влезем и в знаменателя“.
И това се прави много просто:

Тоест, в този случай знаменателят е изкуствено умножен по 7 и разделен на същите седем. Сега записът придоби позната форма.
Когато задачата се съставя на ръка, препоръчително е да се отбележи първата забележителна граница с обикновен молив:

Какво стана? Всъщност ограденият израз се превърна в единица и изчезна в продукта:

Сега остава само да се отървем от триетажната фракция:

Който е забравил опростяването на многоетажните дроби, моля, опреснете материала в справочника Горещи училищни математически формули .

Готов. Окончателен отговор:

Ако не искате да използвате маркировки с молив, тогава решението може да бъде форматирано по следния начин:

“

Използваме първата забележителна граница

“

Пример 2

Намерете границата

Отново виждаме дроб и синус в границата. Опитваме се да заменим нула в числителя и знаменателя:

Наистина имаме несигурност и следователно трябва да се опитаме да организираме първата забележителна граница. На урока Ограничения. Примери за решенияразгледахме правилото, че когато имаме несигурност, тогава трябва да разложим числителя и знаменателя на фактори. Тук - същото, ще представим степените като произведение (множители):

Подобно на предишния пример, ние очертаваме с молив чудесните граници (тук има две от тях) и показваме, че те клонят към една:

Всъщност отговорът е готов:

В следващите примери няма да правя изкуство в Paint, мисля как правилно да съставя решение в тетрадка - вече разбирате.

Пример 3

Намерете границата

Заменяме нула в израза под знака за граница:

Получена е несигурност, която трябва да бъде разкрита. Ако в границата има тангенс, тогава той почти винаги се преобразува в синус и косинус според добре известната тригонометрична формула (между другото, те правят приблизително същото с котангенса, вижте по-долу). методически материал Горещо тригонометрични формули На страницата Математически формули, таблици и справочни материали).

В такъв случай:

Косинусът от нула е равен на едно и е лесно да се отървете от него (не забравяйте да отбележите, че клони към едно):

Така, ако в границата косинусът е МНОЖИТЕЛ, тогава, грубо казано, той трябва да се превърне в единица, която изчезва в произведението.

Тук всичко се оказа по-просто, без никакви умножения и деления. Първата забележителна граница също се превръща в единство и изчезва в продукта:

В резултат на това се получава безкрайност, случва се.

Пример 4

Намерете границата

Опитваме се да заменим нула в числителя и знаменателя:

Получена несигурност (косинус от нула, както помним, е равен на едно)

Използваме тригонометричната формула. Да вземат под внимание! По някаква причина ограниченията, използващи тази формула, са много често срещани.

Изваждаме постоянните множители отвъд иконата за ограничение:

Нека организираме първия забележителен лимит:

Тук имаме само едно прекрасно ограничение, което се превръща в едно и изчезва в продукта:

Да се ​​отървем от триетажния:

Границата всъщност е решена, показваме, че оставащият синус клони към нула:

Пример 5

Намерете границата

Този пример е по-сложен, опитайте се да го разберете сами:

Някои граници могат да бъдат намалени до първата забележителна граница чрез промяна на променливата, можете да прочетете за това малко по-късно в статията Методи за решаване на граници.

Втората прекрасна граница

В теорията на математическия анализ е доказано, че:

Този факт се нарича второ забележително ограничение.

Справка: е ирационално число.

Не само променлива може да действа като параметър, но и сложна функция. Важно е само да се стреми към безкрайност.

Пример 6

Намерете границата

Когато изразът под знака за граница е в сила - това е първият знак, че трябва да се опитате да приложите втората прекрасна граница.

Но първо, както винаги, се опитваме да заместваме безкрайно голямо числов израза, по какъв принцип се прави това, беше анализирано в урока Ограничения. Примери за решения.

Лесно е да се види, че когато основата на степента и показателят - , тоест има несигурност на формата:

Тази несигурност се разкрива само с помощта на втората забележителна граница. Но, както често се случва, втората прекрасна граница не лежи на сребърен поднос и трябва да бъде изкуствено организирана. Можете да разсъждавате по следния начин: в този пример параметърът означава, че трябва да организираме и индикатора. За да направим това, повдигаме основата на степен и за да не се промени изразът, го повдигаме на степен:

Когато задачата е съставена на ръка, отбелязваме с молив:

Почти всичко е готово, ужасната степен се е превърнала в красиво писмо:

В същото време самата икона на лимита се премества в индикатора:

Пример 7

Намерете границата

внимание! Този тип лимит е много често срещан, моля, проучете внимателно този пример.

Опитваме се да заменим безкрайно голямо число в израза под знака за граница:

Резултатът е несигурност. Но второто забележително ограничение се отнася до несигурността на формата. Какво да правя? Трябва да конвертирате основата на степента. Ние разсъждаваме така: в знаменателя имаме , което означава, че трябва да организираме и в числителя.

Има няколко прекрасни граници, но най-известните са първата и втората чудесни граници. Забележителното при тези лимити е, че те се използват широко и могат да се използват за намиране на други лимити, срещани при множество проблеми. Това е, което ще правим в практическата част на този урок. За да се решат проблемите чрез намаляване до първата или втората забележителна граница, не е необходимо да се разкриват съдържащите се в тях несигурности, тъй като стойностите на тези граници отдавна са изведени от велики математици.

Първата забележителна границанаречена граница на съотношението на синуса на безкрайно малка дъга към същата дъга, изразено в радианова мярка:

Нека да преминем към решаването на задачи на първата забележителна граница. Забележка: ако една тригонометрична функция е под знака за граница, това е почти сигурен знак, че този израз може да бъде намален до първата забележителна граница.

Пример 1Намерете границата.

Решение. Вместо това заместване хнула води до несигурност:

.

Знаменателят е синус, следователно изразът може да бъде намален до първата забележителна граница. Да започнем трансформацията:

.

В знаменателя - синус от три x, а в числителя има само едно x, което означава, че трябва да получите три x в числителя. За какво? Да представя 3 х = аи вземете израза.

И стигаме до вариант на първата забележителна граница:

защото няма значение коя буква (променлива) в тази формула е вместо X.

Умножаваме x по три и веднага разделяме:

.

В съответствие с отбелязаното първо забележително ограничение, заместваме дробния израз:

Сега най-накрая можем да решим тази граница:

.

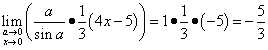Пример 2Намерете границата.

Решение. Директното заместване отново води до несигурността „нула, делене на нула“:

.

За да получим първата забележителна граница, е необходимо х под знака синус в числителя и само х в знаменателя да са с еднакъв коефициент. Нека този коефициент е равен на 2. За да направите това, представете си текущия коефициент при x, както е показано по-долу, извършвайки действия с дроби, получаваме:

.

Пример 3Намерете границата.

Решение. При заместване отново получаваме несигурността "нула, разделена на нула":

.

Вероятно вече разбирате, че от оригиналния израз можете да получите първата прекрасна граница, умножена по първата прекрасна граница. За да направим това, разлагаме квадратите на х в числителя и синуса в знаменателя на едни и същи множители и за да получим еднакви коефициенти за х и синуса, разделяме х в числителя на 3 и веднага умножете по 3. Получаваме:

.

Пример 4Намерете границата.

Решение. Отново получаваме несигурността "нула, разделена на нула":

.

Можем да получим съотношението на първите две забележителни граници. Разделяме и числителя, и знаменателя на x. След това, за да съвпаднат коефициентите при синуси и при x, умножаваме горното x по 2 и веднага делим на 2, а долното x умножаваме по 3 и веднага делим на 3. Получаваме:

Пример 5Намерете границата.

Решение. И отново, несигурността на "нула, разделена на нула":

Спомняме си от тригонометрията, че тангенсът е съотношението на синуса към косинуса, а косинусът на нулата е равен на едно. Правим трансформации и получаваме:

.

Пример 6Намерете границата.

Решение. Тригонометричната функция под знака за граница отново подсказва идеята за прилагане на първата забележителна граница. Представяме го като съотношението на синус към косинус.

Първата забележителна граница се нарича следното равенство:

\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)

Тъй като за $\alpha\to(0)$ имаме $\sin\alpha\to(0)$, казваме, че първата забележителна граница разкрива неопределеност на формата $\frac(0)(0)$. Най-общо казано във формула (1) вместо променливата $\alpha$ под знака синус и в знаменателя може да се намира всеки израз, стига да са изпълнени две условия:

1. Изразите под знака синус и в знаменателя едновременно клонят към нула, т.е. има несигурност от формата $\frac(0)(0)$.
2. Изразите под знака синус и в знаменателя са еднакви.

Следствията от първата забележителна граница също често се използват:

\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \край (уравнение)

На тази страница са решени единадесет примера. Пример № 1 е посветен на доказателството на формули (2)-(4). Примери #2, #3, #4 и #5 съдържат решения с подробни коментари. Примери 6-10 съдържат решения с малко или никакви коментари, тъй като подробните обяснения бяха дадени в предишните примери. При решаването се използват някои тригонометрични формули, които могат да бъдат намерени.

Отбелязвам, че наличието на тригонометрични функции, съчетано с несигурността на $\frac (0) (0)$, не означава, че трябва да се приложи първото забележително ограничение. Понякога са достатъчни прости тригонометрични трансформации - например вижте.

Пример #1

Докажете, че $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

а) Тъй като $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, тогава:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

Тъй като $\lim_(\alpha\to(0))\cos(0)=1$ и $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, тогава:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

б) Нека направим замяната $\alpha=\sin(y)$. Тъй като $\sin(0)=0$, тогава от условието $\alpha\to(0)$ имаме $y\to(0)$. В допълнение, има околност на нула, където $\arcsin\alpha=\arcsin(\sin(y))=y$, така че:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

Равенството $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ е доказано.

в) Нека направим замяната $\alpha=\tg(y)$. Тъй като $\tg(0)=0$, условията $\alpha\to(0)$ и $y\to(0)$ са еквивалентни. В допълнение, има околност на нула, където $\arctg\alpha=\arctg\tg(y))=y$, следователно, разчитайки на резултатите от точка а), ще имаме:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

Равенството $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ е доказано.

Равенствата a), b), c) често се използват заедно с първата забележителна граница.

Пример #2

Изчислете лимит $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.

Тъй като $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ и $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, т.е. и числителят и знаменателят на дробта едновременно клонят към нула, тогава тук имаме работа с несигурност от формата $\frac(0)(0)$, т.е. изпълнени. Освен това може да се види, че изразите под знака синус и в знаменателя са еднакви (т.е. и е изпълнено):

Така че и двете условия, изброени в началото на страницата, са изпълнени. От това следва, че формулата е приложима, т.е. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.

Отговор: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.

Пример #3

Намерете $\lim_(x\to(0))\frac(\sin(9x))(x)$.

Тъй като $\lim_(x\to(0))\sin(9x)=0$ и $\lim_(x\to(0))x=0$, имаме работа с несигурност от формата $\frac( 0 )(0)$, т.е. изпълнени. Изразите под знака синус и в знаменателя обаче не съвпадат. Тук е необходимо да коригирате израза в знаменателя до желаната форма. Трябва изразът $9x$ да бъде в знаменателя - тогава той ще стане верен. По принцип пропускаме фактора $9$ в знаменателя, който не е толкова труден за въвеждане, просто умножете израза в знаменателя по $9$. Естествено, за да компенсирате умножението с $9$, ще трябва веднага да разделите на $9$ и да разделите:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x) $$

Сега изразите в знаменателя и под знака за синус са еднакви. И двете условия за границата $\lim_(x\to(0))\frac(\sin(9x))(9x)$ са изпълнени. Следователно $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. А това означава, че:

$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

Отговор: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

Пример #4

Намерете $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.

Тъй като $\lim_(x\to(0))\sin(5x)=0$ и $\lim_(x\to(0))\tg(8x)=0$, тук имаме работа с неопределеност на форма $\frac(0)(0)$. Въпреки това, формата на първата забележителна граница е нарушена. Числителят, съдържащ $\sin(5x)$, изисква $5x$ в знаменателя. В тази ситуация най-лесният начин е да разделите числителя на $5x$ и веднага да умножите по $5x$. Освен това ще извършим подобна операция със знаменателя, като умножим и разделим $\tg(8x)$ на $8x$:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

Намалявайки с $x$ и изваждайки константата $\frac(5)(8)$ от знака за граница, получаваме:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

Имайте предвид, че $\lim_(x\to(0))\frac(\sin(5x))(5x)$ напълно удовлетворява изискванията за първата забележителна граница. За намиране на $\lim_(x\to(0))\frac(\tg(8x))(8x)$ е приложима следната формула:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$

Отговор: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.

Пример #5

Намерете $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.

Тъй като $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (припомнете си, че $\cos(0)=1$) и $\ lim_(x\to(0))x^2=0$, тогава имаме работа с неопределеност от формата $\frac(0)(0)$. Въпреки това, за да приложите първата чудесна граница, трябва да се отървете от косинуса в числителя, като отидете на синуси (за да приложите след това формулата) или тангенси (за да приложите след това формулата). Можете да направите това със следната трансформация:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$

Да се ​​върнем на лимита:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$

Дробта $\frac(\sin^2(5x))(x^2)$ вече е близо до формата, необходима за първата забележителна граница. Нека поработим малко с дробта $\frac(\sin^2(5x))(x^2)$, коригирайки я до първата чудесна граница (обърнете внимание, че изразите в числителя и под синуса трябва да съвпадат):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$

Да се ​​върнем към разглежданата граница:

$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$

Отговор: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

Пример #6

Намерете границата $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.

Тъй като $\lim_(x\to(0))(1-\cos(6x))=0$ и $\lim_(x\to(0))(1-\cos(2x))=0$, тогава имаме работа с несигурността на $\frac(0)(0)$. Нека го отворим с помощта на първия забележителен лимит. За да направим това, нека преминем от косинуси към синуси. Тъй като $1-\cos(2\alpha)=2\sin^2(\alpha)$, тогава:

$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

Превръща се в даден лимиткъм синусите ще имаме:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$

Отговор: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

Пример #7

Изчисляване на лимит $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ при $\alpha\neq\ бета $.

Подробни обяснения бяха дадени по-рано, но тук просто отбелязваме, че отново има неопределеност на $\frac(0)(0)$. Нека преминем от косинуси към синуси, използвайки формулата

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

Използвайки горната формула, получаваме:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\дясно| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ бета(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ алфа^2-\бета^2)(2)\cdot(1)\cdot(1) =\frac(\бета^2-\алфа^2)(2). $$

Отговор: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ алфа^2)(2)$.

Пример #8

Намерете границата $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.

Тъй като $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (припомнете си, че $\sin(0)=\tg(0)=0$) и $\ lim_(x\to(0))x^3=0$, тогава тук имаме работа с неопределеност от формата $\frac(0)(0)$. Нека го разбием по следния начин:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$

Отговор: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.

Пример #9

Намерете границата $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.

Тъй като $\lim_(x\to(3))(1-\cos(x-3))=0$ и $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, тогава има неопределеност във формата $\frac(0)(0)$. Преди да преминете към нейното разширяване, е удобно да промените променливата по такъв начин, че новата променлива да клони към нула (обърнете внимание, че променливата $\alpha \to 0$ във формулите). Най-лесният начин е да въведете променливата $t=x-3$. Въпреки това, за удобство на по-нататъшни трансформации (тази полза може да се види в хода на решението по-долу), струва си да направите следната замяна: $t=\frac(x-3)(2)$. Отбелязвам, че и двете замествания са приложими в този случай, само второто заместване ще ви позволи да работите по-малко с дроби. Тъй като $x\to(3)$, тогава $t\to(0)$.

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\right| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

Отговор: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.

Пример #10

Намерете границата $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2 )$.

Отново имаме работа с несигурността на $\frac(0)(0)$. Преди да преминете към нейното разширяване, удобно е да направите промяна на променливата по такъв начин, че новата променлива да клони към нула (имайте предвид, че във формулите променливата е $\alpha\to(0)$). Най-лесният начин е да въведете променливата $t=\frac(\pi)(2)-x$. Тъй като $x\to\frac(\pi)(2)$, тогава $t\to(0)$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$

Отговор: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.

Пример #11

Намерете граници $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\) pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

В този случай не е нужно да използваме първата прекрасна граница. Моля, обърнете внимание: както в първата, така и във втората граница има само тригонометрични функции и числа. Често в примери от този вид е възможно да се опрости изразът, разположен под знака за ограничение. В този случай, след споменатото опростяване и намаляване на някои фактори, несигурността изчезва. Дадох този пример само с една цел: да покажа, че наличието на тригонометрични функции под знака за граница не означава непременно прилагането на първата забележителна граница.

Тъй като $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (припомнете си, че $\sin\frac(\pi)(2)=1$ ) и $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (припомнете си, че $\cos\frac(\pi)(2)=0$), тогава имаме работа с несигурност под формата $\frac(0)(0)$. Това обаче изобщо не означава, че трябва да използваме първата забележителна граница. За да се разкрие несигурността, е достатъчно да се вземе предвид, че $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$

Подобно решение има в книгата с решения на Демидович (№ 475). Що се отнася до втората граница, както в предишните примери от този раздел, имаме несигурност от формата $\frac(0)(0)$. Защо възниква? Възниква, защото $\tg\frac(2\pi)(3)=-\sqrt(3)$ и $2\cos\frac(2\pi)(3)=-1$. Ние използваме тези стойности, за да трансформираме изрази в числителя и знаменателя. Целта на нашите действия: напишете сумата в числителя и знаменателя като продукт. Между другото, често е удобно да промените променлива в подобна форма, така че новата променлива да клони към нула (вижте например примери № 9 или № 10 на тази страница). В този пример обаче няма смисъл да се заменя променливата, въпреки че е лесно да се приложи замяната на променливата $t=x-\frac(2\pi)(3)$, ако желаете.

$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4 )(\sqrt(3)). $$

Както можете да видите, не трябваше да прилагаме първото прекрасно ограничение. Разбира се, това може да се направи при желание (вижте бележката по-долу), но не е необходимо.

Какво би било решението, използвайки първото забележително ограничение? Покажи скрий

Използвайки първата забележителна граница, получаваме:

$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\десен))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ дясно))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$

Отговор: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.