Розрахунок дисперсії у статистиці. Залишкова дисперсія

Для згрупованих даних залишкова дисперсія- середня із внутрішньогрупових дисперсій:

Де σ 2 j - внутрішньогрупова дисперсія j-ї групи.

Для не згрупованих даних залишкова дисперсія– міра точності апроксимації, тобто. наближення лінії регресії до вихідних даних:
де y(t) – прогноз рівняння тренда; yt – вихідний ряд динаміки; n - кількість точок; p – число коефіцієнтів рівняння регресії (кількість змінних, що пояснюють).
У цьому прикладі вона називається незміщена оцінка дисперсії.

Приклад №1. Розподіл робітників трьох підприємств одного об'єднання за тарифними розрядами характеризується такими даними:

Тарифний розряд робітника	Чисельність робітників на підприємстві
Тарифний розряд робітника	підприємство 1	підприємство 2	підприємство 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Визначити:
1. дисперсію по кожному підприємству (внутрішньогрупові дисперсії);
2. середню із внутрішньогрупових дисперсій;
3. міжгрупову дисперсію;
4. загальну дисперсію.

Рішення.
Перш ніж приступити до вирішення завдання необхідно з'ясувати, яка ознака є результативною, а якою є факторною. У прикладі результативною ознакою є «Тарифний розряд», а факторною ознакою – «Номер (назва) підприємства».
Тоді маємо три групи (підприємства), для яких необхідно розрахувати групову середню та внутрішньогрупові дисперсії:

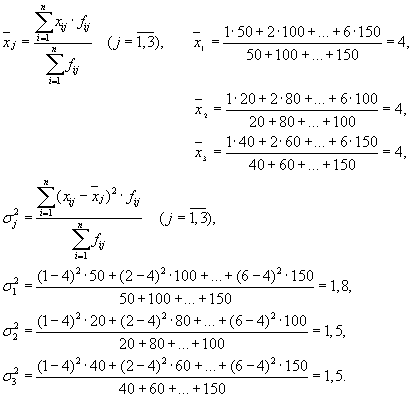
Підприємство	Групова середня,	Внутрішньогрупова дисперсія,
1	4	1,8

Середня з внутрішньогрупових дисперсій ( залишкова дисперсія) розрахуємо за формулою:

де можна розрахувати:

або:

тоді:
Загальна дисперсія дорівнюватиме: s 2 = 1,6 + 0 = 1,6.
Загальну дисперсію також можна розрахувати і за однією з наступних двох формул:

При вирішенні практичних завданьчасто доводиться мати справу з ознакою, яка приймає лише два альтернативні значення. У цьому випадку говорять не про вагу того чи іншого значення ознаки, а про його частку в сукупності. Якщо частку одиниць сукупності, які мають досліджувану ознаку, позначити через « р», а не володіють – через « q», то дисперсію можна розрахувати за такою формулою:
s 2 = p×q

Приклад №2. За даними про вироблення шести робочих бригади визначити міжгрупову дисперсію та оцінити вплив робочої зміни на їх продуктивність праці, якщо загальна дисперсія дорівнює 12,2.

№ робітника бригади	Вироблення робітника, шт.
№ робітника бригади	в I зміну	у II зміну
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Рішення. Початкові дані

X	f 1	f 2	f 3	f 4	f 5	f 6	Разом
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Разом	31	33	37	37	40	38

Тоді маємо 6 групи, для яких необхідно розрахувати групову середню та внутрішньогрупові дисперсії.
1. Знаходимо середні значення кожної групи.

2. Знаходимо середнє квадратичне кожної групи.

Результати розрахунку зведемо до таблиці:

Номер групи	Групова середня	Внутрішньогрупова дисперсія
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Внутрішньогрупова дисперсіяхарактеризує зміну (варіацію) досліджуваної (результативної) ознаки в межах групи під впливом на нього всіх факторів, крім фактора, покладеного в основу угруповання:
Середню із внутрішньогрупових дисперсій розрахуємо за формулою:

4. Міжгрупова дисперсія характеризує зміну (варіацію) досліджуваного (результативного) ознаки під впливом нього чинника (факторного ознаки), покладеного в основу угруповання.
Міжгрупову дисперсію визначимо як:

де

Тоді

Загальна дисперсіяхарактеризує зміна (варіацію) досліджуваного (результативного) ознаки під впливом нею всіх без винятку чинників (факторних ознак). За умовою завдання вона дорівнює 12.2.
Емпіричне кореляційне відношення вимірює, яку частину загальної коливання результативної ознаки викликає фактор, що вивчається. Це відношення факторної дисперсії до загальної дисперсії:

Визначаємо емпіричне кореляційне відношення:

Зв'язки між ознаками можуть бути слабкими та сильними (тісними). Їхні критерії оцінюються за шкалою Чеддока:
0.1 0.3 0.5 0.7 0.9 У нашому прикладі зв'язок між ознакою Y фактором X слабкий
Коефіцієнт детермінації.

Визначимо коефіцієнт детермінації:

Таким чином, на 0.67% варіація обумовлена відмінностями між ознаками, а на 99.37% іншими факторами.
Висновок: у разі вироблення робочих залежить від роботи у конкретну зміну, тобто. вплив робочої зміни з їхньої продуктивність праці не значний і зумовлено іншими чинниками.

Приклад №3. На основі даних про середню заробітної платиі квадратах відхилень від її величини по двох групах робітників знайти загальну дисперсію, застосувавши правило додавання дисперсій:

Рішення:
Середня із внутрішньогрупових дисперсій

Міжгрупову дисперсію визначимо як:

Загальна дисперсія дорівнюватиме: 480 + 13824 = 14304

Теорія ймовірності – особливий розділ математики, який вивчають лише студенти вищих навчальних закладів. Ви любите розрахунки та формули? Вас не лякають перспективи знайомства з нормальним розподілом, ентропією ансамблю, математичним очікуванням та дисперсією дискретною випадкової величини? Тоді цей предмет вам буде дуже цікавим. Познайомимося з кількома найважливішими базовими поняттями цього розділу науки.

Згадаймо основи

Навіть якщо ви пам'ятаєте найпростіші поняття теорії ймовірності, не зневажайте перших абзаців статті. Справа в тому, що без чіткого розуміння основ ви не зможете працювати з формулами, що розглядаються далі.

Отже, відбувається деяка випадкова подія, якийсь експеримент. Через війну вироблених дій ми можемо отримати кілька результатів - одні зустрічаються частіше, інші - рідше. Імовірність події - це відношення кількості реально отриманих наслідків одного типу до загальному числуможливих. Тільки знаючи класичне визначенняданого поняття, ви зможете приступити до вивчення математичного очікуваннята дисперсії безперервних випадкових величин.

Середнє арифметичне

Ще в школі на уроках математики ви починали працювати із середнім арифметичним. Це поняття широко використовується в теорії ймовірності, і тому його не можна обминути. Головним для нас зараз є те, що ми зіткнемося з ним у формулах математичного очікування та дисперсії випадкової величини.

Ми маємо послідовність чисел і хочемо знайти середнє арифметичне. Все, що від нас вимагається - підсумувати все існуюче та розділити на кількість елементів у послідовності. Нехай ми маємо числа від 1 до 9. Сума елементів дорівнюватиме 45, і це значення ми розділимо на 9. Відповідь: - 5.

Дисперсія

Говорячи науковою мовою, дисперсія – це середній квадрат відхилень отриманих значень ознаки від середньої арифметичної. Позначається одна заголовною латинською літерою D. Що потрібно, щоб її розрахувати? Для кожного елемента послідовності порахуємо різницю між наявним числом та середнім арифметичним і зведемо у квадрат. Значень вийде рівно стільки, скільки може бути результатів у події, що ми розглядаємо. Далі ми підсумовуємо все отримане та ділимо на кількість елементів у послідовності. Якщо у нас можливі п'ять наслідків, то ділимо на п'ять.

У дисперсії є й властивості, які потрібно запам'ятати, щоб застосовувати під час вирішення завдань. Наприклад, зі збільшенням випадкової величини у X разів, дисперсія збільшується у X у квадраті разів (т. е. X*X). Вона ніколи не буває менше нуля і не залежить від зсуву значень на рівне значення у більшу чи меншу сторону. Крім того, для незалежних випробуваньдисперсія суми дорівнює сумі дисперсій.

Тепер нам обов'язково слід розглянути приклади дисперсії дискретної випадкової величини та математичного очікування.

Припустимо, що ми провели 21 експеримент та отримали 7 різних результатів. Кожен із них ми спостерігали, відповідно, 1,2,2,3,4,4 та 5 разів. Чому дорівнюватиме дисперсія?

Спочатку порахуємо середнє арифметичне: сума елементів, зрозуміло, дорівнює 21. Ділимо її на 7, отримуючи 3. Тепер із кожного числа вихідної послідовності віднімемо 3, кожне значення зведемо в квадрат, а результати складемо разом. Вийде 12. Тепер нам залишається розділити число на кількість елементів, і, начебто, все. Але є проблема! Давайте її обговоримо.

Залежність кількості експериментів

Виявляється, при розрахунку дисперсії у знаменнику може стояти одне з двох чисел: або N або N-1. Тут N - це число проведених експериментів або число елементів у послідовності (що, по суті, те саме). Від чого це залежить?

Якщо кількість випробувань вимірюється сотнями, ми повинні ставити в знаменник N. Якщо одиницями, то N-1. Кордон вчені вирішили провести досить символічно: на сьогоднішній день вона проходить за цифрою 30. Якщо експериментів ми провели менше 30, то ділити суму будемо на N-1, а якщо більше – то на N.

Завдання

Давайте повернемося до нашого прикладу розв'язання задачі на дисперсію та математичне очікування. Ми отримали проміжне число 12, яке потрібно було поділити на N або N-1. Оскільки експериментів ми провели 21, що менше 30 виберемо другий варіант. Отже, відповідь: дисперсія дорівнює 12/2 = 2.

Математичне очікування

Перейдемо до другого поняття, яке ми обов'язково маємо розглянути цій статті. Математичне очікування - це результат складання всіх можливих наслідків, помножених на відповідні ймовірності. Важливо розуміти, що отримане значення, як і результат розрахунку дисперсії, виходить лише один раз для цілого завдання, скільки результатів у ній не розглядалося.

Формула математичного очікування досить проста: беремо результат, множимо з його ймовірність, додаємо те саме для другого, третього результату тощо. буд. Усе, що з цим поняттям, розраховується нескладно. Наприклад, сума матожиданий дорівнює маточку суми. Для твору актуально те саме. Такі прості операції дозволяє із собою виконувати далеко не кожна величина теорії ймовірності. Давайте візьмемо завдання і порахуємо значення одразу двох вивчених понять. Крім того, ми відволікалися на теорію - настав час попрактикуватися.

Ще один приклад

Ми провели 50 випробувань і отримали 10 видів результатів – цифри від 0 до 9 – які з'являються у різному відсотковому відношенні. Це відповідно: 2%, 10%, 4%, 14%, 2%, 18%, 6%, 16%, 10%, 18%. Нагадаємо, що для отримання ймовірностей потрібно розділити значення у відсотках на 100. Таким чином отримаємо 0,02; 0,1 і т.д. Представимо для дисперсії випадкової величини та математичного очікування приклад розв'язання задачі.

Середнє арифметичне розрахуємо за такою формулою, яку пам'ятаємо з молодшої школи: 50/10 = 5.

Тепер переведемо ймовірність у кількість наслідків «в штуках», щоб було зручніше рахувати. Отримаємо 1, 5, 2, 7, 1, 9, 3, 8, 5 і 9. З кожного отриманого значення віднімемо середнє арифметичне, після чого кожен із отриманих результатів зведемо в квадрат. Подивіться, як це зробити, з прикладу першого елемента: 1 - 5 = (-4). Далі: (-4) * (-4) = 16. Для решти значень проробіть ці операції самостійно. Якщо ви все зробили правильно, то після додавання всіх ви отримаєте 90.

Продовжимо розрахунок дисперсії та математичного очікування, розділивши 90 на N. Чому ми вибираємо N, а не N-1? Правильно тому, що кількість проведених експериментів перевищує 30. Отже: 90/10 = 9. Дисперсію ми отримали. Якщо у вас вийшло інше число, не засмучуйтесь. Швидше за все, ви припустилися банальної помилки при розрахунках. Перевірте ще раз написане, і напевно все встане на свої місця.

Зрештою, згадаємо формулу математичного очікування. Не будемо наводити всіх розрахунків, напишемо лише відповідь, з якою ви зможете звіритися, закінчивши всі необхідні процедури. Матоожидання дорівнюватиме 5,48. Нагадаємо лише, як здійснювати операції, з прикладу перших елементів: 0*0,02 + 1*0,1… тощо. Як бачите, ми просто множимо значення результату з його ймовірність.

Відхилення

Ще одне поняття, тісно пов'язане з дисперсією та математичним очікуванням – середнє квадратичне відхилення. Позначається воно або латинськими літерами sd, або грецькою малої «сигмою». Це поняття показує, наскільки у середньому відхиляються значення від центральної ознаки. Щоб знайти її значення, потрібно розрахувати квадратний коріньіз дисперсії.

Якщо ви збудуєте графік нормального розподілуі захочете побачити безпосередньо на ньому квадратичного відхилення, це можна зробити за кілька етапів. Візьміть половину зображення зліва або праворуч від моди (центрального значення), проведіть перпендикуляр до горизонтальної осі так, щоб площі фігур були рівні. Величина відрізка між серединою розподілу і проекцією, що вийшла, на горизонтальну вісь і буде середнім квадратичним відхиленням.

Програмне забезпечення

Як видно з описів формул і наведених прикладів, розрахунки дисперсії та математичного очікування - не найпростіша процедура з арифметичної точки зору. Щоб не витрачати час, є сенс скористатися програмою, яка використовується у вищих навчальних закладах- вона називається "R". У ній є функції, що дозволяють розраховувати значення для багатьох понять із статистики та теорії ймовірності.

Наприклад, ви задаєте вектор значень. Робиться це так: vector<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.

На закінчення

Дисперсія та математичне очікування - це без яких складно надалі щось розрахувати. В основному курсі лекцій у вишах вони розглядаються вже у перші місяці вивчення предмета. Саме через нерозуміння цих найпростіших понять та невміння їх розрахувати багато студентів відразу починають відставати за програмою і пізніше отримують погані позначки за результатами сесії, що позбавляє їх стипендії.

Потренуйтесь хоча б один тиждень по півгодини на день, вирішуючи завдання, схожі на представлені в цій статті. Тоді на будь-якій контрольній теорії ймовірності ви впораєтеся з прикладами без сторонніх підказок і шпаргалок.

Дисперсія - це міра розсіювання, що описує порівняльне відхилення між значеннями даних та середньою величиною. Є найбільш використовуваною мірою розсіювання в статистиці, що обчислюється шляхом підсумовування, зведеного квадрат, відхилення кожного значення даних від середньої величини. Формула для обчислення дисперсії представлена нижче:

s 2 – дисперсія вибірки;

x ср - середнє значення вибірки;

n — розмір вибірки (кількість значень даних),

(x i - x ср) - відхилення від середньої величини для кожного значення набору даних.

Для кращого розуміння формули розберемо приклад. Я не дуже люблю готування, тому заняттям цим займаюся дуже рідко. Проте, щоб не померти з голоду, час від часу мені доводиться підходити до плити для реалізації задуму щодо насичення мого організму білками, жирами та вуглеводами. Набір даних, поданий нижче, показує, скільки разів Ренат готує їжу щомісяця:

Першим кроком при обчисленні дисперсії є визначення середнього значення вибірки, яке в прикладі дорівнює 7,8 рази на місяць. Інші обчислення можна полегшити за допомогою наступної таблиці.

Фінальна фаза обчислення дисперсії виглядає так:

Для тих, хто любить робити всі обчислення за один раз, рівняння виглядатиме так:

Використання методу «сирого рахунку» (приклад із готуванням)

Існує ефективніший спосіб обчислення дисперсії, відомий як метод «сирого рахунку». Хоча з першого погляду рівняння може здатися дуже громіздким, насправді воно не таке страшне. Можете в цьому переконатись, а потім і вирішіть, який метод вам більше подобається.

- Сума кожного значення даних після зведення в квадрат,

- Квадрат суми всіх значень даних.

Не втрачайте розум прямо зараз. Дозвольте уявити все це у вигляді таблиці, і тоді ви побачите, що обчислень тут менше, ніж у попередньому прикладі.

Як бачите, результат вийшов той самий, що й під час використання попереднього методу. Переваги даного методу стають очевидними зі збільшенням розміру вибірки (n).

Розрахунок дисперсії в Excel

Як ви вже, напевно, здогадалися, в Excel є формула, що дозволяє розрахувати дисперсію. Причому, починаючи з Excel 2010, можна знайти 4 різновиди формули дисперсії:

1) ДИСП.В - Повертає дисперсію за вибіркою. Логічні значення та текст ігноруються.

2) ДИСП.Г - Повертає дисперсію по генеральній сукупності. Логічні значення та текст ігноруються.

3) ДИСПА - Повертає дисперсію за вибіркою з урахуванням логічних та текстових значень.

4) ДИСПРА - Повертає дисперсію по генеральній сукупності з урахуванням логічних та текстових значень.

Для початку розберемося в різниці між вибіркою та генеральною сукупністю. Призначення описової статистики у тому, щоб підсумовувати чи відображати дані те щоб оперативно отримувати загальну картину, так би мовити, огляд. Статистичний висновок дозволяє робити висновки про будь-яку сукупність на основі вибірки даних із цієї сукупності. Сукупність є всі можливі результати чи виміри, які становлять нам інтерес. Вибірка - це підмножина сукупності.

Наприклад, нас цікавить сукупність групи студентів одного з Російських ВНЗ, і нам необхідно визначити середній бал групи. Ми можемо порахувати середню успішність студентів, і тоді отримана цифра буде параметром, оскільки в наших розрахунках буде задіяна ціла сукупність. Однак якщо ми хочемо розрахувати середній бал усіх студентів нашої країни, тоді ця група буде нашою вибіркою.

Різниця у формулі розрахунку дисперсії між вибіркою та сукупністю полягає у знаменнику. Де для вибірки він дорівнюватиме (n-1), а для генеральної сукупності тільки n.

Тепер розберемося з функціями розрахунку дисперсії із закінченнями А,в описі яких сказано, що при розрахунку враховуються текстові та логічні значення. В даному випадку при розрахунку дисперсії певного масиву даних, де зустрічаються не числові значення, Excel інтерпретуватиме текстові та хибні логічні значення як рівними 0, а справжні логічні значення як рівними 1.

Отже, якщо у вас є масив даних, розрахувати його дисперсію не складе ніяких труднощів, скориставшись однією з перерахованих вище функцій Excel.

Дисперсією (розсіянням) випадкової величини називається математичне очікування квадрата відхилення випадкової величини від її математичного очікування:

Для обчислення дисперсії можна використовувати трохи перетворену формулу

так як М(Х), 2 та
- Постійні величини. Таким чином,

4.2.2. Властивості дисперсії

Властивість 1.Дисперсія постійної величини дорівнює нулю. Справді, за визначенням

Властивість 2.Постійний множник можна виносити за знак дисперсії зі зведенням їх у квадрат.

Доведення

Центрованою випадковою величиною називається відхилення випадкової величини від її математичного очікування:

Центрована величина має дві зручні для перетворення властивості:

Властивість 3.Якщо випадкові величини Х і Yнезалежні, то

Доведення. Позначимо
. Тодії.

У другому доданку з незалежності випадкових величин і властивостей центрованих випадкових величин

приклад 4.5.Якщо aі b- постійні, тоD (aХ+b)= D(aХ)+D(b)=
.

4.2.3. Середнє квадратичне відхилення

Дисперсія як характеристика розкиду випадкової величини має один недолік. Якщо, наприклад, Х– помилка виміру має розмірність ММ, то дисперсія має розмірність
. Тому часто вважають за краще користуватися іншою характеристикою розкиду – середнім квадратичним відхиленням , яке дорівнює кореню квадратному з дисперсії

Середнє квадратичне відхилення має таку ж розмірність, як і сама випадкова величина.

Приклад 4.6.Дисперсія числа появи події у схемі незалежних випробувань

Виготовляється nнезалежних випробувань та ймовірність появи події у кожному випробуванні дорівнює р. Висловимо, як і раніше, кількість появи події Хчерез число появи події в окремих дослідах:

Так як досліди незалежні, то і пов'язані з дослідами випадкові величини незалежні. А через незалежність маємо

Але кожна із випадкових величин має закон розподілу (приклад 3.2)

і
(Приклад 4.4). Тому, за визначенням дисперсії:

де q=1- p.

У результаті маємо
,

Середнє квадратичне відхилення числа події в nнезалежних дослідах одно
.

4.3. Моменти випадкових величин

Крім вже розглянутих, випадкові величини мають безліч інших числових характеристик.

Початковим моментом k Х (
) називається математичне очікування k-й ступеня цієї випадкової величини

Центральним моментом k-го порядку випадкової величини Хназивається математичне очікування k-ой ступеня відповідної центрованої величини.

Легко бачити, що центральний момент першого порядку завжди дорівнює нулю, центральний момент другого порядку дорівнює дисперсії, оскільки .

Центральний момент третього порядку дає уявлення про асиметрію розподілу випадкової величини. Моменти порядку вище за другий використовуються порівняно рідко, тому ми обмежимося лише самими поняттями про них.

4.4. Приклади знаходження законів розподілу

Розглянемо приклади знаходження законів розподілу випадкових величин та його числових характеристик.

Приклад 4.7.

Скласти закон розподілу числа влучень у ціль при трьох пострілах по мішені, якщо ймовірність влучення при кожному пострілі дорівнює 0,4. Знайти інтегральну функцію F(х)для отриманого розподілу дискретної випадкової величини Хта накреслити її графік. Знайти математичне очікування M(X) , дисперсію D(X) та середнє квадратичне відхилення
(Х) випадкової величини X.

Рішення

1) Дискретна випадкова величина Х– кількість попадань у ціль при трьох пострілах – може набувати чотирьох значень: 0, 1, 2, 3 . Імовірність того, що вона прийме кожне з них, знайдемо за формулою Бернуллі за: n=3,p=0,4,q=1- p=0,6 та m=0, 1, 2, 3:

Отримаємо ймовірність можливих значень Х:;

Складемо шуканий закон розподілу випадкової величини Х:

Контроль: 0,216 +0,432 +0,288 +0,064 = 1.

Побудуємо багатокутник розподілу отриманої випадкової величини Х. Для цього у прямокутній системі координат відзначимо точки (0; 0,216), (1; 0,432), (2; 0,288), (3; 0,064). З'єднаємо ці точки відрізками прямих, отримана ламана і є багатокутник розподілу, що шукається (рис. 4.1).

2) Якщо х 0, то F(х)=0. Дійсно, значень, менших за нуль, величина Хне приймає. Отже, при всіх х0 , користуючись визначенням F(х), отримаємо F(х)=P(X< x) =0 (як імовірність неможливої події).

Якщо 0 , то F(X) =0,216. Дійсно, у цьому випадку F(х)=P(X< x) = =P(- < X 0)+ P(0< X< x) =0,216+0=0,216.

Якщо взяти, наприклад, х=0,2, то F(0,2)=P(X<0,2) . Але ймовірність події Х<0,2 равна 0,216, так как случайная величинаХлише в одному випадку набуває значення менше 0,2, а саме 0 із ймовірністю 0,216.

Якщо 1 , то

Справді, Хможе прийняти значення 0 з ймовірністю 0,216 та значення 1 з ймовірністю 0,432; отже, одне з цих значень, байдуже яке, Хможе прийняти (за теоремою складання ймовірностей несумісних подій) з ймовірністю 0,648.

Якщо 2 , То міркуючи аналогічно, отримаємо F(х)= 0,216 +0,432 + + 0,288 = 0,936. Справді, нехай, наприклад, х=3. Тоді F(3)=P(X<3) висловлює ймовірність події X<3 – стрелок сделает меньше трех попаданий, т.е. ноль, один или два. Применяя теорему сложения вероятностей, получим указанное значение функцииF(х).

Якщо x>3, то F(х)= 0,216 +0,432 +0,288 +0,064 = 1. Дійсно, подія X
є достовірним і ймовірність його дорівнює одиниці, а X>3 – неможливим. Враховуючи що

F(х)=P(X< x) =P(X 3) + P(3< X< x) , Отримаємо зазначений результат.

Отже, отримано шукану інтегральну функцію розподілу випадкової величини Х:

F(x) =

графік якої зображено на рис. 4.2.

3) Математичне очікування дискретної випадкової величини дорівнює сумі творів усіх можливих значень Хна їх ймовірності:

М(Х)=0=1,2.

Тобто в середньому відбувається одне влучення в ціль при трьох пострілах.

Дисперсію можна обчислити, виходячи з визначення дисперсії D(X)= M(X- M(X)) або скористатися формулою D(X)= M(X
яка веде до мети швидше.

Напишемо закон розподілу випадкової величини Х :

Знайдемо математичне очікування для Х:

М(Х ) = 04
= 2,16.

Обчислимо шукану дисперсію:

D(X) = M(X ) – (M(X)) = 2,16 – (1,2)= 0,72.

Середнє квадратичне відхилення знайдемо за формулою

(X) =
= 0,848.

Інтервал ( M- ; M+ ) = (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – інтервал найімовірніших значень випадкової величини Х, До нього потрапляють значення 1 і 2.

приклад 4.8.

Дана диференціальна функція розподілу (функція густини) безперервної випадкової величини Х:

f(x) =

1) Визначити постійний параметр a.

2) Знайти інтегральну функцію F(x) .

3) Побудувати графіки функцій f(x) і F(x) .

4) Знайти двома способами ймовірності Р(0,5< X 1,5) і P(1,5< X<3,5) .

5). Знайти математичне очікування М(Х), дисперсію D(Х)та середнє квадратичне відхилення
випадкової величини Х.

Рішення

1) Диференціальна функція за якістю f(x) має задовольняти умові
.

Обчислимо цей невласний інтеграл для цієї функції f(x) :

Підставляючи цей результат у ліву частину рівності, отримаємо, що а=1. В умови для f(x) замінимо параметр ана 1:

2) Для знаходження F(x) скористаємося формулою

Якщо х
, то
, отже,

Якщо 1
то

Якщо x>2, то

Отже, шукана інтегральна функція F(x) має вигляд:

3) Побудуємо графіки функцій f(x) і F(x) (Рис. 4.3 та 4.4).

4) Імовірність потрапляння випадкової величини у заданий інтервал (а,b) обчислюється за формулою
, якщо відома функція f(x), і за формулою P(a < X < b) = F(b) – F(a), якщо відома функція F(x).

Знайдемо
за двома формулами та порівняємо результати. За умовою а=0,5;b=1,5; функція f(X) задана у пункті 1). Отже, шукана ймовірність за формулою дорівнює:

Та ж ймовірність може бути обчислена за формулою b) через збільшення отриманої в п.2). інтегральної функції F(x) на цьому інтервалі:

Так як F(0,5)=0.

Аналогічно знаходимо

так як F(3,5)=1.

5) Для знаходження математичного очікування М(Х)скористаємося формулою
Функція f(x) задана у рішенні пункту 1), вона дорівнює нулю поза інтервалом (1,2]: