При розрахунку дисперсії середнє значення ознаки розраховується. Як порахувати дисперсію випадкової величини
Однак цієї характеристики ще мало для дослідження випадкової величини. Уявимо двох стрільців, які стріляють по мішені. Один стріляє влучно і потрапляє близько до центру, а інший просто розважається і навіть не цілиться. Але що кумедно, його середнійрезультат буде таким самим, як і в першого стрілка! Цю ситуацію умовно ілюструють такі випадкові величини:
«Снайперське» математичне очікування рівне, проте й у «цікавої особистості»: воно теж нульове!
Таким чином, виникає потреба кількісно оцінити, наскільки далеко розпорошенікулі (значення випадкової величини) щодо центру мішені ( математичного очікування). Ну а розсіюванняз латині перекладається не інакше, як дисперсія .
Подивимося, як визначається ця числова характеристикаодному з прикладів 1-ї частини уроку: 
Там ми знайшли невтішне математичне очікування цієї гри, і зараз ми маємо обчислити її дисперсію, яка позначаєтьсячерез.
З'ясуємо, наскільки далеко розкидані виграші/програші щодо середнього значення. Очевидно, що для цього потрібно вирахувати різниціміж значеннями випадкової величиниі її математичним очікуванням:
–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5
Тепер начебто потрібно підсумувати результати, але цей шлях не годиться – тому, що коливання вліво взаємознижуватимуться з коливаннями вправо. Так, наприклад, у стрільця-«любителя» (Приклад вище)різниці складуть ![]() , і при додаванні дадуть нуль, тому ніякої оцінки розсіювання його стрілянини ми не отримаємо.
, і при додаванні дадуть нуль, тому ніякої оцінки розсіювання його стрілянини ми не отримаємо.
Щоб обійти цю неприємність, можна розглянути модулірізниць, але з технічних причин прижився підхід, коли їх зводять у квадрат. Рішення зручніше оформити таблицею: 
І тут напрошується вирахувати середньозваженезначення квадратів відхилень. А це що таке? Це їх математичне очікування, яке і є мірилом розсіювання:
![]() – визначеннядисперсії. З визначення одразу зрозуміло, що дисперсія не може бути негативною- Візьміть на замітку для практики!
– визначеннядисперсії. З визначення одразу зрозуміло, що дисперсія не може бути негативною- Візьміть на замітку для практики!
Згадуємо, як знаходити матожидання. Розмножуємо квадрати різниць на відповідні ймовірності (продовження таблиці):
– образно кажучи, це «сила тяги»,
та підсумовуємо результати:
Чи не здається вам, що на тлі виграшів результат вийшов завеликим? Все вірно - ми зводили в квадрат, і щоб повернутися до розмірності нашої гри, потрібно витягти квадратний корінь. Ця величина називається середнім квадратичним відхиленням
і позначається грецькою літерою"сигма":
Іноді це значення називають стандартним відхиленням .
У чому його зміст? Якщо ми відхилимося від математичного очікування вліво та вправо на середнє квадратичне відхилення:![]()
– то цьому інтервалі будуть «сконцентровані» найімовірніші значення випадкової величини. Що ми, власне, і спостерігаємо:
Проте так склалося, що з аналізі розсіювання майже завжди оперують поняттям дисперсії. Давайте розберемося, що вона означає стосовно ігор. Якщо у випадку зі стрілками йдеться про «купність» попадань щодо центру мішені, то дисперсія характеризує дві речі:
По-перше, очевидно, що зі збільшенням ставок, дисперсія теж зростає. Так, наприклад, якщо ми збільшимо у 10 разів, то математичне очікування збільшиться у 10 разів, а дисперсія – у 100 разів (якщо це квадратична величина). Але, зауважте, що самі правила гри не змінилися! Змінилися лише ставки, грубо кажучи, раніше ми ставили 10 карбованців, тепер 100.
Другий, цікавіший момент полягає в тому, що дисперсія характеризує стиль гри. Подумки зафіксуємо ігрові ставки на якомусь певному рівні, і подивимося, що тут до чого:
Гра з низькою дисперсією – це обережна гра. Гравець схильний вибирати найнадійніші схеми, де за 1 раз він не програє/виграє занадто багато. Наприклад, система «червоне/чорне» в рулетці (див. Приклад 4 статті Випадкові величини) .
Гра із високою дисперсією. Її часто називають дисперсійноїгрою. Це авантюрний чи агресивний стиль гри, де гравець обирає "адреналінові" схеми. Згадаймо хоча б «Мартінгейл», в якому на кону виявляються суми, що на порядки перевершують «тиху» гру попереднього пункту.
Показовою є ситуація в покері: тут є так звані тайтовігравці, які схильні обережно і «труситися» над своїми ігровими засобами (Банкролом). Не дивно, що їхній банкрол не піддається значним коливанням (низька дисперсія). Навпаки, якщо у гравця висока дисперсія, це агресор. Він часто ризикує, робить великі ставки і може, як зірвати величезний банк, так і програтися вщент.
Те саме відбувається на Форексі, і так далі – прикладів маса.
Причому, у всіх випадках не важливо – чи на копійки йде гра, чи на тисячі доларів. На будь-якому рівні є свої низько- та високодисперсійні гравці. Ну, а за середній виграш, як ми пам'ятаємо, «відповідає» математичне очікування.
Напевно, ви помітили, що знаходження дисперсії – процес тривалий і копіткий. Але математика щедра:
Формула для знаходження дисперсії
Ця формула виводиться безпосередньо з визначення дисперсії, і ми негайно пускаємо їх у оборот. Скопіюю зверху табличку з нашою грою: 
і знайдене маточування.
Обчислимо дисперсію другим способом. Спочатку знайдемо математичне очікування – квадрата випадкової величини. за визначення математичного очікування:
В даному випадку:
Таким чином, за формулою:
Як кажуть, відчуйте різницю. І на практиці, звичайно, краще застосовувати формулу (якщо іншого не потребує умова).
Освоюємо техніку рішення та оформлення:
Приклад 6

Знайти її математичне очікування, дисперсію та середнє квадратичне відхилення.
Це завдання зустрічається повсюдно, і, зазвичай, йде без змістовного сенсу.
Можете уявляти кілька лампочок з числами, які загоряються в дурдомі з певними ймовірностями:)
Рішення: Основні обчислення зручно звести до таблиці Спочатку у верхні два рядки записуємо вихідні дані. Потім розраховуємо твори, потім і, нарешті, суми у правому стовпці: 
Власне, майже все готове. У третьому рядку намалювалося готове математичне очікування: ![]() .
.
Дисперсію обчислимо за такою формулою:
І, нарешті, середнє квадратичне відхилення:
- особисто я зазвичай округляю до 2 знаків після коми.
Усі обчислення можна провести на калькуляторі, а ще краще – в Екселі:
ось тут вже важко помилитися:)
Відповідь:
Бажаючі можуть ще більше спростити своє життя та скористатися моїм калькулятором (Демо), який не тільки миттєво вирішить це завдання, а й побудує тематичні графіки (скоро дійдемо). Програму можна скачати в бібліотеці- якщо ви завантажили хоча б один навчальний матеріал, або отримати іншим способом. Дякуємо за підтримку проекту!
Пара завдань для самостійного вирішення:
Приклад 7
Обчислити дисперсію випадкової величини попереднього прикладу визначення.
І аналогічний приклад:
Приклад 8
Дискретна випадкова величина задана своїм законом розподілу:

Так, значення випадкової величини бувають досить великими (Приклад із реальної роботи), і тут, по можливості, використовуйте Ексель. Як, до речі, і в Прімері 7 – це швидше, надійніше та приємніше.
Рішення та відповіді внизу сторінки.
На закінчення 2-ї частини уроку розберемо ще одне типове завдання, можна сказати, невеликий ребус:
Приклад 9
Дискретна випадкова величина може набувати лише два значення: і , причому . Відома ймовірність, математичне очікування та дисперсія.
Рішення: почнемо з невідомої ймовірності Так як випадкова величина може прийняти лише два значення, то сума ймовірностей відповідних подій:
і оскільки, то.
Залишилося знайти …, легко сказати:) Але так гаразд, понеслося. За визначенням математичного очікування: ![]() - Підставляємо відомі величини:
- Підставляємо відомі величини:
![]() - І більше з цього рівняння нічого не вичавити, хіба що можна переписати його у звичному напрямку:
- І більше з цього рівняння нічого не вичавити, хіба що можна переписати його у звичному напрямку: ![]()

або: ![]()
Про подальші дії, гадаю, ви здогадуєтеся. Складемо і вирішимо систему: 
Десяткові дроби- це, звичайно, повне неподобство; множимо обидва рівняння на 10: 
і ділимо на 2: 
Ось так то краще. З 1-го рівняння виражаємо: ![]() (Це більш простий шлях)- Підставляємо в 2-е рівняння:
(Це більш простий шлях)- Підставляємо в 2-е рівняння:
![]()
Зводимо у квадратта проводимо спрощення: 
Помножуємо на: 
В результаті отримано квадратне рівняння, знаходимо його дискримінант:
- Чудово!
і у нас виходить два рішення:
1) якщо ![]() , то
, то ![]() ;
;
2) якщо ![]() , то.
, то.
Умові задовольняє перша пара значень. З високою ймовірністю все правильно, проте запишемо закон розподілу: 
і виконаємо перевірку, а саме, знайдемо матожидання:
 .
.
Назад, якщо - невід'ємна п.в. функція, така що  , то є абсолютно безперервна ймовірнісна міра на така, що є її щільністю.
, то є абсолютно безперервна ймовірнісна міра на така, що є її щільністю.
Заміна заходу в інтегралі Лебега:
 ,
,
де будь-яка борелівська функція, що інтегрується щодо ймовірнісної міри .
Дисперсія, види та властивості дисперсії Поняття дисперсії
Дисперсія у статистицізнаходиться як середнє квадратичне відхилення індивідуальних значень ознаки у квадраті від середньої арифметичної. Залежно від вихідних даних вона визначається за формулами простої та зваженої дисперсій:
1. Проста дисперсія(Для несгрупованих даних) обчислюється за формулою:
![]()
2. Зважена дисперсія (для варіаційного ряду):

де n – частота (повторюваність фактора Х)
Приклад знаходження дисперсії
На цій сторінці описано стандартний приклад знаходження дисперсії, також Ви можете переглянути інші завдання на її знаходження
Приклад 1. Визначення групової, середньої з групової, міжгрупової та загальної дисперсії
Приклад 2. Знаходження дисперсії та коефіцієнта варіації у групувальній таблиці
Приклад 3. Знаходження дисперсії у дискретному ряду
Приклад 4. Є такі дані щодо групи з 20 студентів заочного відділення. Потрібно побудувати інтервальний ряд розподілу ознаки, розрахувати середнє значення ознаки та вивчити його дисперсію

Побудуємо інтервальне угруповання. Визначимо розмах інтервалу за формулою:
![]()
де X max - максимальне значення групувального ознаки; X min-мінімальне значення групувальної ознаки; n – кількість інтервалів:
Приймаємо n=5. Крок дорівнює: h = (192 - 159) / 5 = 6,6
Складемо інтервальне угруповання

Для подальших розрахунків збудуємо допоміжну таблицю:

X"i - середина інтервалу. (наприклад середина інтервалу 159 - 165,6 = 162,3)
Середню величину зростання студентів визначимо за формулою середньої арифметичної зваженої:

Визначимо дисперсію за такою формулою:
Формулу можна перетворити так:

З цієї формули випливає, що дисперсія дорівнює різниці середньої з квадратів варіантів і квадрата та середньої.
Дисперсія у варіаційних рядах з рівними інтервалами за способом моментів може бути розрахована наступним способом при використанні другої властивості дисперсії (розділивши всі варіанти на величину інтервалу). Визначення дисперсії, обчисленої за способом моментів, за такою формулою менш трудомісткий:

де i – величина інтервалу; А - умовний нуль, як який зручно використовувати середину інтервалу, що володіє найбільшою частотою; m1 – квадрат моменту першого порядку; m2 – момент другого порядку
Дисперсія альтернативної ознаки (якщо в статистичній сукупності ознака змінюється так, що є тільки два варіанти, що взаємно виключають один одного, то така мінливість називається альтернативною) може бути обчислена за формулою:

Підставляючи до цієї формули дисперсії q =1- р, отримуємо:

Види дисперсії
Загальна дисперсіявимірює варіацію ознаки у всій сукупності загалом під впливом всіх чинників, що зумовлюють цю варіацію. Вона дорівнює середньому квадрату відхилень окремих значень ознаки х від загального середнього значення х може бути визначена як проста дисперсія або зважена дисперсія.
Внутрішньогрупова дисперсія характеризує випадкову варіацію, тобто. частина варіації, яка обумовлена впливом неврахованих факторів і не залежить від ознаки-фактора, покладеної в основу угруповання. Така дисперсія дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи X від середньої арифметичної групи і може бути обчислена як проста дисперсія або зважена дисперсія.
Таким чином, внутрішньогрупова дисперсія вимірюєваріацію ознаки всередині групи та визначається за формулою:

де хі - групова середня; ni – число одиниць у групі.
Наприклад, внутрішньогрупові дисперсії, які треба визначити в задачі вивчення впливу кваліфікації робітників на рівень продуктивності праці в цеху показують варіації виробітку в кожній групі, викликані всіма можливими факторами (технічний стан обладнання, забезпеченість інструментами та матеріалами, вік робітників, інтенсивність праці тощо) .), крім відмінностей у кваліфікаційному розряді (всередині групи всі робітники мають одну й ту саму кваліфікацію).
Середня всередині групових дисперсій відображає випадкову варіацію, тобто ту частину варіації, яка відбувалася під впливом всіх інших факторів, за винятком фактора угруповання. Вона розраховується за такою формулою:

Міжгрупова дисперсіяхарактеризує систематичну варіацію результативної ознаки, яка обумовлена впливом ознаки-фактора, покладеного в основу угруповання. Вона дорівнює середньому квадрату відхилень групових середніх від загальної середньої. Міжгрупова дисперсіярозраховується за формулою:

Де σ 2 j - внутрішньогрупова дисперсія j-ї групи.
Для не згрупованих даних залишкова дисперсія– міра точності апроксимації, тобто. наближення лінії регресії до вихідних даних: 
де y(t) – прогноз рівняння тренда; yt – вихідний ряд динаміки; n - кількість точок; p – число коефіцієнтів рівняння регресії (кількість змінних, що пояснюють).
У цьому прикладі вона називається незміщена оцінка дисперсії.
Приклад №1. Розподіл робітників трьох підприємств одного об'єднання за тарифними розрядами характеризується такими даними:
| Тарифний розряд робітника | Чисельність робітників на підприємстві | ||
| підприємство 1 | підприємство 2 | підприємство 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Визначити:
1. дисперсію по кожному підприємству (внутрішньогрупові дисперсії);
2. середню із внутрішньогрупових дисперсій;
3. міжгрупову дисперсію;
4. загальну дисперсію.
Рішення.
Перш ніж приступити до вирішення завдання необхідно з'ясувати, яка ознака є результативною, а якою є факторною. У прикладі результативною ознакою є «Тарифний розряд», а факторною ознакою – «Номер (назва) підприємства».
Тоді маємо три групи (підприємства), для яких необхідно розрахувати групову середню та внутрішньогрупові дисперсії:

| Підприємство | Групова середня, | Внутрішньогрупова дисперсія, |
| 1 | 4 | 1,8 |
Середня з внутрішньогрупових дисперсій ( залишкова дисперсія) розрахуємо за формулою:
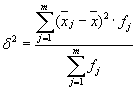
де можна розрахувати:

або:

тоді:
Загальна дисперсія дорівнюватиме: s 2 = 1,6 + 0 = 1,6.
Загальну дисперсію також можна розрахувати і за однією з наступних двох формул:

При вирішенні практичних завданьчасто доводиться мати справу з ознакою, яка приймає лише два альтернативні значення. У цьому випадку говорять не про вагу того чи іншого значення ознаки, а про його частку в сукупності. Якщо частку одиниць сукупності, які мають досліджувану ознаку, позначити через « р», а не володіють – через « q», то дисперсію можна розрахувати за такою формулою:
s 2 = p×q
Приклад №2. За даними про вироблення шести робочих бригади визначити міжгрупову дисперсію та оцінити вплив робочої зміни на їх продуктивність праці, якщо загальна дисперсія дорівнює 12,2.
| № робітника бригади | Вироблення робітника, шт. | |
| в I зміну | у II зміну | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Рішення. Початкові дані
| X | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | Разом |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Разом | 31 | 33 | 37 | 37 | 40 | 38 |
Тоді маємо 6 групи, для яких необхідно розрахувати групову середню та внутрішньогрупові дисперсії.
1. Знаходимо середні значення кожної групи.
2. Знаходимо середнє квадратичне кожної групи.
Результати розрахунку зведемо до таблиці:
| Номер групи | Групова середня | Внутрішньогрупова дисперсія |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Внутрішньогрупова дисперсіяхарактеризує зміну (варіацію) досліджуваної (результативної) ознаки в межах групи під впливом на нього всіх факторів, крім фактора, покладеного в основу угруповання:
Середню із внутрішньогрупових дисперсій розрахуємо за формулою:
4. Міжгрупова дисперсіяхарактеризує зміну (варіацію) досліджуваного (результативного) ознаки під впливом нього чинника (факторного ознаки), покладеного в основу угруповання.
Міжгрупову дисперсію визначимо як:
де
Тоді
Загальна дисперсіяхарактеризує зміна (варіацію) досліджуваного (результативного) ознаки під впливом нею всіх без винятку чинників (факторних ознак). За умовою завдання вона дорівнює 12.2.
Емпіричне кореляційне відношення вимірює, яку частину загальної коливання результативної ознаки викликає фактор, що вивчається. Це відношення факторної дисперсії до загальної дисперсії:
Визначаємо емпіричне кореляційне відношення:
Зв'язки між ознаками можуть бути слабкими та сильними (тісними). Їхні критерії оцінюються за шкалою Чеддока:
0.1 0.3 0.5 0.7 0.9 У нашому прикладі зв'язок між ознакою Y фактором X слабкий
Коефіцієнт детермінації.
Визначимо коефіцієнт детермінації:
Таким чином, на 0.67% варіація обумовлена відмінностями між ознаками, а на 99.37% іншими факторами.
Висновок: у разі вироблення робочих залежить від роботи у конкретну зміну, тобто. вплив робочої зміни з їхньої продуктивність праці не значний і зумовлено іншими чинниками.
Приклад №3. На основі даних про середню заробітної платиі квадратах відхилень від її величини по двох групах робітників знайти загальну дисперсію, застосувавши правило додавання дисперсій:
Рішення:Середня із внутрішньогрупових дисперсій
Міжгрупову дисперсію визначимо як:
Загальна дисперсія дорівнюватиме: 480 + 13824 = 14304
Обчислимо вMSEXCELдисперсію та стандартне відхиленнявибірки. Також обчислимо дисперсію випадкової величини, якщо відомий її розподіл.
Спочатку розглянемо дисперсію, потім стандартне відхилення.
Дисперсія вибірки
Дисперсія вибірки (вибіркова дисперсія,samplevariance) характеризує розкид значень у масиві щодо .
Усі 3 формули математично еквівалентні.
З першої формули видно, що дисперсія вибіркице сума квадратів відхилень кожного значення в масиві від середнього, Поділена на розмір вибірки мінус 1.
дисперсії вибіркивикористовується функція ДИСП(), англ. назва VAR, тобто. VARiance. З версії MS EXCEL 2010 рекомендується використовувати аналог ДИСП.В() , англ. назва VARS, тобто. Sample VARiance. Крім того, починаючи з версії MS EXCEL 2010 є функція ДИСП.Г(), англ. назва VARP, тобто. Population VARiance, яка обчислює дисперсіюдля генеральної сукупності . Вся відмінність зводиться до знаменника: замість n-1 як у ДИСП.В(), у ДИСП.Г() у знаменнику просто n. До MS EXCEL 2010 для обчислення дисперсії генеральної сукупності використовувалась функція ДИСПР().
Дисперсію вибірки
=КВАДРОТКЛ(Вибірка)/(РАХУНОК(Вибірка)-1)
=(СУММКВ(Вибірка)-РАХУНОК(Вибірка)*СРЗНАЧ(Вибірка)^2)/ (РАХУНОК(Вибірка)-1)- Звичайна формула
= СУМ((Вибірка-СРЗНАЧ(Вибірка))^2)/ (РАХУНОК(Вибірка)-1) –
Дисперсія вибіркидорівнює 0, тільки в тому випадку, якщо всі значення рівні між собою і відповідно рівні середнього значення. Зазвичай, ніж більша величина дисперсіїтим більше розкид значень у масиві.
Дисперсія вибіркиє точковою оцінкою дисперсіїрозподілу випадкової величини, з якої було зроблено вибірка. Про побудову довірчих інтервалів при оцінці дисперсіїможна прочитати у статті.
Дисперсія випадкової величини
Щоб обчислити дисперсіювипадкової величини необхідно знати її .
Для дисперсіївипадкової величини Х часто використовують позначення Var(Х). Дисперсіядорівнює квадрату відхилення від середнього E(X): Var(Х)=E[(X-E(X)) 2 ]
дисперсіяобчислюється за такою формулою:

де x i – значення, яке може набувати випадкова величина, а μ – середнє значення (), р(x) – ймовірність, що випадкова величина прийме значення х.
Якщо випадкова величина має, то дисперсіяобчислюється за такою формулою:

Розмірність дисперсіївідповідає квадрату одиниці виміру вихідних значень. Наприклад, якщо значення у вибірці є вимірювання ваги деталі (в кг), то розмірність дисперсії буде кг 2 . Це буває складно інтерпретувати, тому для характеристики розкиду значень частіше використовують рівну величину квадратного кореняз дисперсії – стандартне відхилення.
Деякі властивості дисперсії:
Var(Х + a) = Var (Х), де Х - випадкова величина, а - константа.
Var(aХ)=a 2 Var(X)
Var(Х)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2
Ця властивість дисперсії використовується в статті про лінійну регресію.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), де Х та Y - випадкові величини, Cov(Х;Y) - коваріація цих випадкових величин.
Якщо випадкові величини незалежні (independent), їх коваріаціядорівнює 0, отже, Var(Х+Y)=Var(Х)+Var(Y). Ця властивість дисперсії використовується при виведенні.
Покажемо, що з незалежних величин Var(Х-Y)=Var(Х+Y). Справді, Var(Х-Y)=Var(Х-Y)=Var(Х+(-Y))=Var(Х)+Var(-Y)=Var(Х)+Var(-Y)=Var( Х)+(-1) 2 Var(Y)=Var(Х)+Var(Y)=Var(Х+Y). Ця властивість дисперсії використовується для побудови.
Стандартне відхилення вибірки
Стандартне відхилення вибірки- це міра того, наскільки широко розкидані значення у вибірці щодо них.
За визначенням, стандартне відхиленняодно квадратному кореню з дисперсії:

Стандартне відхиленняне враховує величину значень у вибірці, а тільки ступінь розсіювання значень навколо них середнього. Щоб проілюструвати це наведемо приклад.
Обчислимо стандартне відхилення для 2-х вибірок: (1; 5; 9) та (1001; 1005; 1009). В обох випадках s=4. Очевидно, що відношення величини стандартного відхилення до значень масиву вибірок істотно відрізняється. Для таких випадків використовується Коефіцієнт варіації(Coefficient of Variation, CV) - ставлення Стандартне відхиленнядо середнього арифметичному, Вираженого у відсотках.
У MS EXCEL 2007 та більш ранніх версіях для обчислення Стандартне відхилення вибіркивикористовується функція = СТАНДОТКЛОН (), англ. назва STDEV, тобто. STandard DEViation. З версії MS EXCEL 2010 рекомендується використовувати її аналог = СТАНДОТКЛОН.В(), англ. назва STDEV.S, тобто. Sample STandard DEViation.
Крім того, починаючи з версії MS EXCEL 2010 є функція СТАНДОТКЛОН.Г() , англ. назва STDEV.P, тобто. Population STandard DEViation, яка обчислює стандартне відхиленнядля генеральної сукупності. Вся відмінність зводиться до знаменника: замість n-1 як у СТАНДОТКЛОН.В() , у СТАНДОТКЛОН.Г() у знаменнику просто n.
Стандартне відхиленняможна також обчислити безпосередньо за нижченаведеними формулами (див. файл прикладу)
=КОРІНЬ(КВАДРОТКЛ(Вибірка)/(РАХУНОК(Вибірка)-1))
=КОРІНЬ((СУММКВ(Вибірка)-РАХУНОК(Вибірка)*СРЗНАЧ(Вибірка)^2)/(РАХУНОК(Вибірка)-1))
Інші заходи розкиду
Функція КВАДРОТКЛ() обчислює з умму квадратів відхилень значень від них середнього. Ця функція поверне той самий результат, як і формула =ДИСП.Г( Вибірка)*РАХУНОК( Вибірка), де Вибірка- Посилання на діапазон, що містить масив значень вибірки (). Обчислення функції КВАДРОТКЛ() проводяться за формулою:

Функція СРОТКЛ() є мірою розкиду безлічі даних. Функція СРОТКЛ() обчислює середнє абсолютних значень відхилень значень від середнього. Ця функція поверне той самий результат, що й формула =СУМПРОВИЗВ(ABS(Вибірка-СРЗНАЧ(Вибірка)))/РАХУНОК(Вибірка), де Вибірка- Посилання на діапазон, що містить масив значень вибірки.
Обчислення функції СРОТКЛ () проводяться за формулою:

Дисперсія у статистиці визначається як середнє квадратичне відхилення індивідуальних значень ознаки у квадраті від середньої арифметичної. Поширений спосіб розрахунку квадратів відхилень варіантів від середньої зі своїми подальшим усередненням.
![]()
В економічно-статистичному аналізі варіацію ознаки прийнято оцінювати найчастіше за допомогою середнього квадратичного відхилення, воно є коренем квадратним з дисперсії.
 (3)
(3)
Характеризує абсолютну коливання значень варіюючого ознаки виявляється у тих самих одиницях виміру, як і варіанти. У статистиці часто виникає необхідність порівняння варіації різних ознак. Для таких порівнянь використовують відносний показник варіації, коефіцієнт варіації.
Властивості дисперсії:
1)якщо з усіх варіант відняти якесь число, то дисперсія від цього не зміниться;
2) якщо всі значення варіант розділити на якесь число b, то дисперсія зменшиться в b^2 разів, тобто.
3) якщо обчислити середній квадрат відхилень від будь-якого числа з нерівного середнього арифметичного, то він буде більше дисперсії . При цьому цілком певну величину на квадрат різниці між середньою величиною поc.
![]()
Дисперсію можна визначити як різницю між середнім квадратом та середньою у квадраті.
17. Групова та міжгрупова варіації. Правило складання дисперсії
Якщо статистична сукупність розбита на групи або частини за ознакою, що вивчається, то для такої сукупності можуть бути обчислені такі види дисперсії: групові (приватні), середньо групові (приватних), і міжгрупова.
Загальна дисперсія- Відображає варіацію ознаки за рахунок всіх умов і причин, що діють у даній статистичній сукупності. ![]()
Групова дисперсія- Дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи від середньої арифметичної цієї групи, званої групової середньої. При цьому групова середня не збігається із загальною середньою для всієї сукупності.
![]()
Групова дисперсія відображає варіацію ознаки лише за рахунок умов та причин, що діють усередині групи.
Середня групова дисперсія- визначається як середнє зважене арифметичне з групових дисперсій, причому вагами є обсяги груп.
Міжгрупова дисперсія- дорівнює середньому квадрату відхилень групових середніх від загальної середньої.
Міжгрупова дисперсія характеризує варіацію результативної ознаки за рахунок групувальної ознаки.
Між розглянутими видами дисперсій існує певне співвідношення: загальна дисперсія дорівнює сумі середньої групової та міжгрупової дисперсії.
Це співвідношення називається правилом складання дисперсії.
18. Динамічний ряд та його складові елементи. Види динамічних рядів.
Ряд у статистиці- це цифрові дані, що показують, зміна явища в часі або в просторі і дають можливість проводити статистичне порівняння явищ як у процесі їх розвитку в часі, так і різним формамта видів процесів. Завдяки цьому можна виявити взаємну залежність явищ.
Процес розвитку руху соціальних явищ у часі у статистиці прийнято називати динамікою. Для відображення динаміки будують ряди динаміки (хронологічні, тимчасові), які являють собою ряди значень статистичного показника, що змінюються в часі (наприклад, кількість засуджених за 10 років), розташованих в хронологічному порядку. Їх складовими елементами є цифрові значення даного показника та періоди чи моменти часу, до яких вони відносяться.
Найважливіша характеристика рядів динаміки- їх розмір (обсяг, величина) того чи іншого явища, досягнутих у певний період або до певного моменту. Відповідно, величина членів низки динаміки - його рівень. Розрізняютьпочатковий, середній та кінцевий рівні динамічного ряду. Початковий рівеньпоказує величину першого, кінцевий – величину останнього члена ряду. Середній рівеньявляє собою середню хронологічну варіаційну раду і обчислюється в залежності від того, чи динамічний ряд є інтервальним або моментним.
Ще одна важлива характеристика динамічного ряду- час, що минув від початкового до кінцевого спостереження, чи кількість таких спостережень.
Існують різні види рядів динаміки, їх можна класифікувати за такими ознаками.
1) Залежно від способу вираження рівнів ряди динаміки поділяються на ряди абсолютних та похідних показників (відносних та середніх величин).
2) Залежно від того, як виражають рівні ряду стан явища на певні моменти часу (на початок місяця, кварталу, року тощо) або його величину за певні інтервали часу (наприклад, за добу, місяць, рік тощо). п.), розрізняють відповідно моментні та інтервальні рядидинаміки. Моментні лави в аналітичній роботі правоохоронних органів використовуються порівняно рідко.
Теоретично статистики виділяють раді динаміки і з інших класифікаційних ознак: залежно від відстані між рівнями - з рівнозначними рівнями і нерівними рівнями у часі; залежно від наявності основної тенденції досліджуваного процесу – стаціонарні та не стаціонарні. При аналізі динамічних рядіввиходять з наступного рівні ряду у вигляді складових:
Y t = TP + Е(t)
де ТР – детермінована складова, що визначає загальну тенденцію зміни в часі або тренд.
Е (t) - випадкова компонента, що викликає коливання рівнів.



