Теорема про нерівність сторін трикутника. Нерівність трикутника. Повні уроки - Гіпермаркет знань
- Нерівність трикутника.
Цілі уроку
- Ознайомитись з новими визначеннями та теоремами пов'язаними з трикутниками.
- Навчитися застосовувати властивості фігур під час вирішення завдань.
- Розвиваючі – розвинути увагу учнів, посидючість, наполегливість, логічне мислення, математичне мовлення.
- Виховні – за допомогою уроку виховувати уважне ставлення один до одного, прищеплювати вміння слухати товаришів, взаємовиручку, самостійність.
Завдання уроку
- Перевірити вміння учнів вирішувати завдання.
План уроку
- З історії математики.
- Повторення раніше вивченого матеріалу.
- Вивчення нового матеріалу.
- Приклад розв'язання задачі.
- Завдання для самостійної перевірки.
З історії математики
Займає почесне місце у вавилонській геометрії, згадка про нього часто зустрічається в папірусі Ахмеса.
Термін гіпотенуза походить від грецького hypoteinsa, що означає тягнеться під чимось, стягує. Слово бере початок від образу давньоєгипетських арф, на яких струни натягувалися на кінці двох взаємно перпендикулярних підставок.
Термін катет походить від грецького слова «катетос», яке означало схильність, перпендикуляр. У середні віки словом катет означали висоту прямокутного трикутника, тоді як інші його сторони називали гіпотенузою, відповідно основою. У XVII столітті слово катет починає застосовуватися в сучасному розумінні і поширюється, починаючи з XVIII століття.
Евклід вживає вирази:
"сторони, що укладають прямий кут", - для катетів;
«сторона, що стягує прямий кут», – для гіпотенузи.
Для початку в темі про нерівність трикутника пропоную згадати те, що вже проходили, освіжити в пам'яті вже вивчене, а саме ознаки рівності трикутників. Почнемо мабуть із історичної довідки про ознаки рівності трикутників. Щоб повністю розібратися в темі, що і як, коли і ким було написано і доведено.
Історична довідка про ознаки рівності трикутників
Якщо ми звернемося до історії, то в першому підручнику з геометрії – «Початках» Евкліда можна знайти таке визначення: «Фігури, що поєднуються один з одним рівні між собою…». Минуло понад дві тисячі років, а визначення не змінилося. Це визначення рівність фігур можна зарахувати і до трикутникам.
– Отже, які трикутники називаються рівними?
- Але чи завжди нам вдається реально поєднати трикутники?
- Справді, іноді поєднати трикутники немає можливості. Що ж робити? Достатньо порівняти лише три елементи одного трикутника з трьома елементами іншого трикутника. Ось тут нам на допомогу прийдуть ознаки рівності трикутників, вони розкажуть, які саме елементи потрібно порівнювати. Що таке ознака рівності трикутників та скільки існує ознак? Деякі умови, у яких два даних трикутника виявляються рівними, називаються ознаками рівності трикутників. Можна сміливо сказати, що ознака – це прикмета, якою можна дізнатися ті чи інші властивості постатей.
Відеоурок «Нерівність трикутника» розкриває зміст та доказ теореми про нерівність трикутника. Завдання даного відеоуроку - полегшити запам'ятовування теореми та наслідки з неї, розуміння та запам'ятовування перебігу міркувань за її доказом.
Високий рівень наочності матеріалу, голосовий супровід дає можливість використовувати цей посібник як самостійну частину уроку, звільняючи час вчителя для поліпшення якості навчання, посилення індивідуальної роботи з учнями.
Відеоурок починається з подання теми та формулювання теореми про нерівність трикутника. Для запам'ятовування затвердження теореми її виведено на екран і виділено кольором. Ця теорема стверджує, що будь-яка сторона трикутника є меншою від суми двох інших його сторін. Доказ затвердження пропонується розглянути на прикладі трикутника Δ, який демонструється під текстом теореми на екрані.
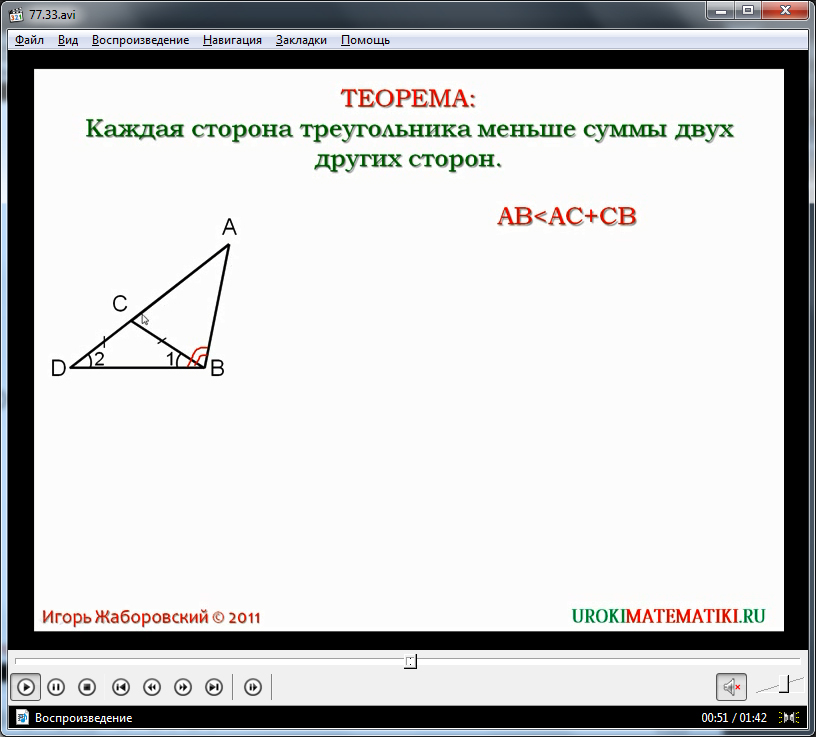
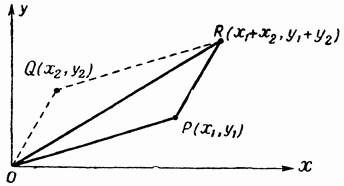
Уточнюється, що для доказу теореми необхідно підтвердити, що сторона AB є меншою від величини суми сторін AC і CB. Дане твердження позначено на екрані виразом AB Освоївши цю теорему, можна розглядати її слідство, яке стверджує, що для будь-яких трьох точок A, B, C, які не належать до однієї прямої, справедливі нерівності: AB Відеоурок «Нерівність трикутника» може бути використаний вчителем на уроці геометрії як наочний посібник або як частина уроку замість пояснення вчителем нової теми. Детальне зрозуміле пояснення замінить вчителя при самостійному вивченні предмета учнем, і навіть допоможе пояснити предмет під час дистанційного навчання. Математичний гурток Русанівського ліцею Нерівність трикутника Нерівність трикутника – один із найважливіших геометричних фактів. Є однією з інтуїтивних властивостей відстані, вона нерідко допомагає у вирішенні непростих геометричних і текстових завдань. За допомогою нерівності трикутника можна відсіяти частину з можливих варіантів розташування будь-яких елементів у громіздких геометричних задачах. Часто саме невиконання суворої нерівності трикутника (а саме – досягнення в ньому рівності) дає підстави стверджувати про належність трьох точок однієї прямої. Таким чином, нерівність трикутника є одночасно інтуїтивно зрозумілою, навіть очевидною, але часто стає потужним інструментом при вирішенні серйозних математичних завдань. Декілька слів про нерівності У математиці нерівністьє твердження про відносну величину або порядок двох об'єктів, що розглядаються, або про те, що вони просто не однакові. Класична нерівність як об'єкт дослідження можна також розглядати як окремий випадок відношення порядку. Розрізняють суворіі несуворінерівності. Або ж, переходячи на мову відносин, сувору нерівність можна вважати ставленням суворого порядку на безлічі дійсних чисел (тобто ставленням, яке має властивості антирефлексивності, антисиметричності та транзитивності). Якщо ж йдеться про сувору нерівність, то можна говорити про нього як про відношення нестрогого порядку на тій самій множині (тобто розглядати замість антирефлексивності рефлексивність). Нагадаємо, що про відносини як математичний об'єкт та їх властивості ми вже згадували в Лекції 7 (були розглянуті властивості відношення ділимості). Докладніше їх вивчення ми маємо в майбутньому, оскільки вони досить успішно систематизують і узагальнюють ряд елементарних математичних понять. Тепер ми наведемо кілька прикладів нерівностей кожного з названих типів. Сувориминерівностями називають такі нерівності: Нерівність трикутника AO + OB > AB; CO + OD > CD. Розглянемо суму AC + BD: AC + BD = (AO + OC) + (BO + OD) = = (AO + BO) + (OC + OD) > AB + CD. Аналогічно: Складаючи всі три нерівності, отримаємо потрібне. Вправа. Доведіть, що медіана AMу довільному трикутнику ABCза довжиною менше, ніж Другий літак пролетить відстань Розглянемо різницю між відстанню, що пролетів перший літак, і відстанню, яку подолав другий. Доведемо, що незалежно від розташування точок A, B, C, Dна площині (міст A, B, C, Dу країні) вираз буде непозитивним. Для цього слід розглянути два випадки. 1. Припустимо, що точки A, B, C, D
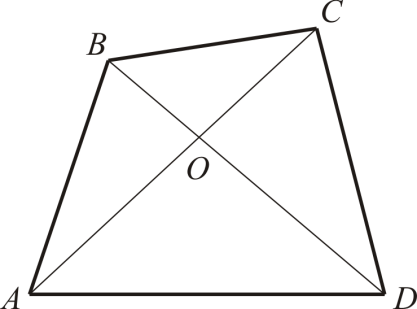
ABCDз діагоналями ACі BD. Тоді запишемо послідовно нерівності трикутника для трикутників ABC, BCD, CDAі DAB(див. рис. 2): AB + BC > AC; BC + CD > BD; CD + DA > CA; DA + AB > DB. Склавши всі чотири нерівності, отримаємо 2. Розглянемо випадок, коли точки A, B, C, D
створюють на площині чотирикутник ACBDз діагоналями ABі CD
(Намалюйте собі відповідний малюнок). Зауважимо, що нерівності трикутника виконуються тих самих трикутників, як у першому випадку. Виявляється, що розв'язання задачі залишиться тим самим, незважаючи на те, що розташування точок на площині суттєво змінилося. Це можна вважати ще однією характерною рисоюбагатьох розв'язків задач, що використовують нерівність трикутника. Отже, перший літак прилетить раніше, оскільки його маршрут коротший за маршрут другого. Зауважте, що рішення Завдання 5 потребує невеликого аналізу, що є неодмінною якістю всіх олімпіадних завдань. Будьте уважні – Ваше вирішення завдання буде правильним лише тоді, коли Ви розглянете усі можливі випадки, які підходять під умову. Слід також зазначити, що найчастіше малюнку, що зображує умова завдання, не видно трикутника, застосування нерівності трикутника якого дало б моментальне рішення. У такому разі може допомогти успішно підібране геометричне перетворення. Про це ми поговоримо дещо пізніше. Знайомство з нерівністю трикутника у цьому слід оголосити закінченим. Але нова зустріч із ним уже не за горами. 7 клас Лекція 13. Нерівність трикутника Фіхте Йоганн Готліб (1762-1814) - один із найвизначніших представників класичної німецької філософії. До книги увійшли відомі роботи: "Факти свідомості", "Призначення людини", "Науковчення" та інші. Яким би зловісним не представлявся у ЗМІ та літературі нинішньому та минулому поколінням націонал-соціалізм, він не перестає привертати до себе уваги мільйонів людей. Символ захисту та влади - ПентаграмаMarsyas Пентаграма є одним з найважливіших магічних символів. Саме це слово походить від грецьких слів "pente", що означає п'ять, і "gramma" - літера; пентаграма - З геометрії ми знаємо, що сума довжин двох сторін трикутника не менше довжинийого третя сторона. Подивимося, як можна висловити цю теорему алгебраїчною. Розглянемо трикутник, розташований так, як показано на рис. 22. Геометрична нерівність рівносильно алгебраїчної нерівності трикутника Чи можна довести останню нерівність, не звертаючись до геометрії? У § 8 гол. III було наведено доказ для одновимірної нагоди (див. теорему 2 гл. III). в якому нерівність набуває наступного вигляду: у цьому записі воно зустрічається частіше, ніж рівносильна йому нерівність Найбільш простий спосіб доказу двовимірного варіанта нерівності трикутника (4.50) полягає в тому, щоб довести рівносильну йому нерівність. Рис. 22. Нерівність трикутника. Для цього зведемо обидві частини нерівності (4.50) у квадрат, при цьому ми прийдемо до нерівності рівносильному (4.50). Легко бачити, що остання нерівність у свою чергу рівносильна наступному: Але це нерівність є простим наслідком відомої нерівності Коші [двовимірний варіант, див. (4.38)] що й доводить нерівність трикутника. Як і в одновимірному випадку, визначення умов, за яких нерівність трикутника (4.50) звертається в рівність, не становить особливих труднощів. Згадаймо, що в нерівності Коші (4.52) рівність досягається тоді й лише тоді, коли пропорційні, тобто коли Нерівність (4.51) може бути отримана шляхом вилучення квадратного кореня з обох частин нерівності (4.52). Ця операція законна, тому що мається на увазі невід'ємний квадратний корінь з виразу, що стоїть зліва. Нехай є негативний квадратний корінь з виразу, що стоїть у правій частині (4.52). У цьому випадку навіть тоді, коли пропорційні, (4.51) матиме місце сувора нерівність. Таким чином, рівність (4.51), а отже, і в нерівності трикутника (4.50) досягається тоді і тільки тоді, коли де неотрицательный коефіцієнт пропорційності. Геометричний зміст цієї умови, необхідної і достатньої для того, щоб у формулі (4.50) мала місце рівність, полягає в наступному: точки (рис. 21) повинні належати одній прямій, причому точки розташовані по одну сторону від точки О. При трикутник перетворюється на відрізок прямий. Інакше висловлюючись, точки як лежать однією прямої з точкою Про, а й лежать одному промені з початком Про. Легко переконатися в тому, що отримані умови узгоджуються з відповідними умовами для одновимірного випадку (нерівності де рівність досягається тоді і тільки тоді, коли числа мають один знак. Доказ нерівності трикутника можна узагальнити, слідуючи тим самим шляхом, що й під час виведення нерівності Гельдера, а саме довести, що нерівність має місце для будь-яких дійсних значень причому, як і раніше, рівність досягається в тому і тільки тому випадку, коли числа пропорційні і коефіцієнт пропорційності позитивний. Ми повернемося до цієї нерівності в гол. VI, де буде розглянуто його геометричне значення. Перейдемо до іншого доказу нерівності трикутника, який можна використовувати також для отримання більш загальних результатів. Має місце тотожність Нерівність Коші у формі, що використовує квадратне коріння[див. (4.51)], застосуємо по черзі до двох виразів.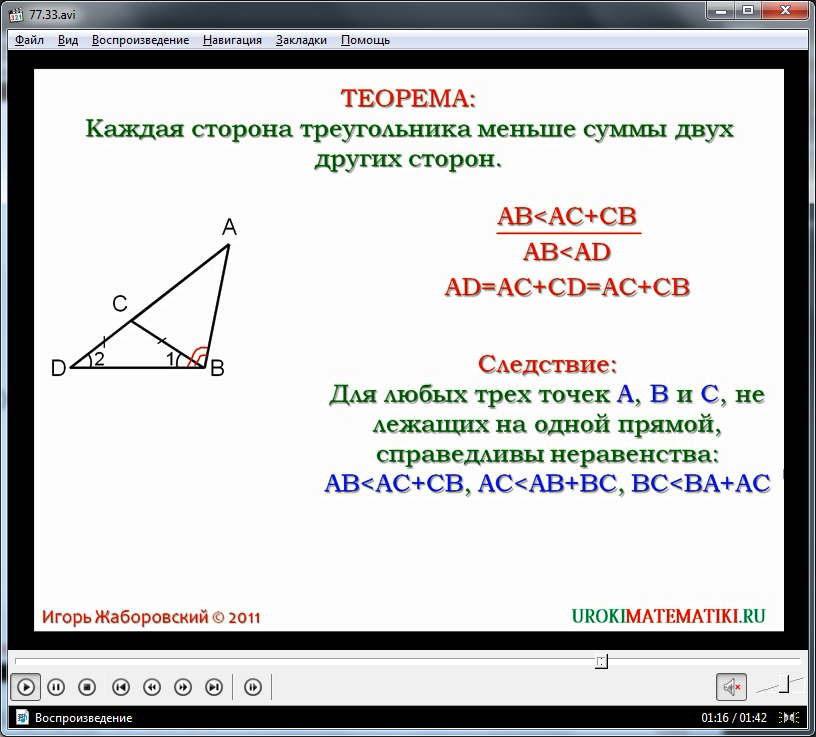
![]()
a < b- означає, що aменшеb; a
> b
- означає, що aбільшеb; a
≠ b- означає, що aне дорівнюєbабо ж що aі b різні.
До несуворимнерівностям відносять такі математичні відносини: a ≤ b- означає, що aменше чи одноbабо, що те саме, aне більше (не перевищує, не перевищує)b; a ≥
b- означає, що aбільше чи одноbабо, що те саме, aне меншеb.
Поки що ми не турбуватимемо себе глибшим дослідженням нерівностей. Сьогодні нам цілком вистачить усталених уявлень про нерівності.
Доказ теореми
. Розглянемо трикутник ABCі покажемо, що AB < AC + BC. За доказом скористаємося одним із видів додаткових побудов – відкладанням рівних відрізків ( метод випрямлення). У трикутнику ABC(рис. 1) на продовженні сторони BCвідкладемо відрізок CD, рівний AC. У рівнобедреному трикутнику ACD
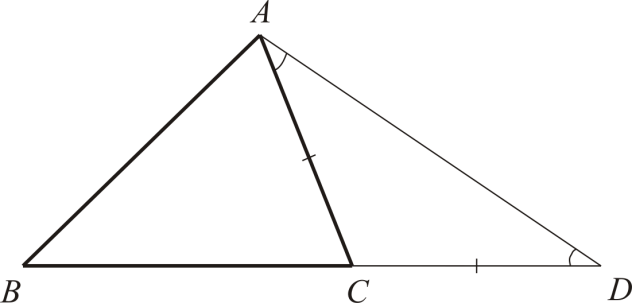
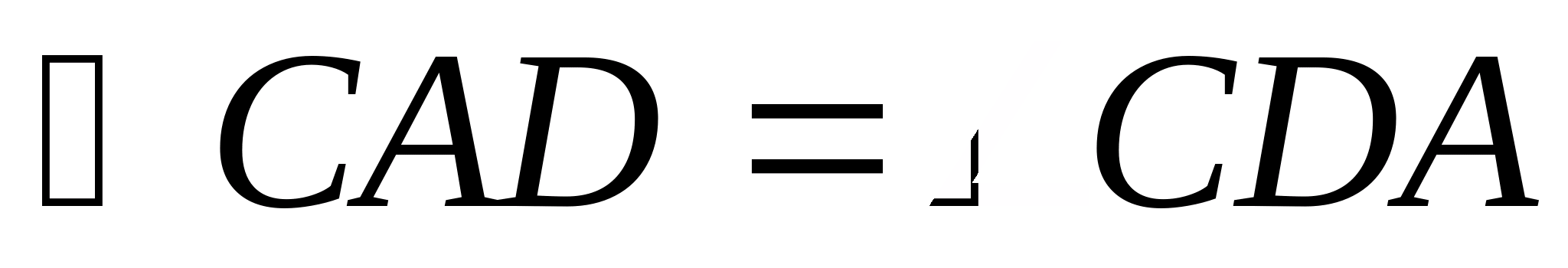 . У трикутнику ABDкут ADBменше кута BADотже, BD > AB, або BC + CD
> AB. Але CD = ACотже, AC + BC > AB. Зауваження. Зверніть увагу, що, виходячи з формулювання теореми, слід записати відразу три нерівності: AB < AC + BC; AC< AB + BC; BC < AB + AC. Нерідко, записавши одну нерівність, про двох інших чомусь забувають. Пам'ятайте, що це може призвести до неприємних помилок. Нерівність трикутника може бути одним із простих критеріїв приналежності трьох точок однієї прямої. Три точки належать одній прямій тоді й лише тоді, коли в нерівності трикутника досягається рівність. Звичайно, рівність може досягатися лише в одній з трьох нерівностей (див. зауваження), оскільки одна з точок лежатиме чітко між двома іншими. Вправа. Доведіть, що у трикутнику кожна сторона більша за різницю двох інших сторін. Наведемо як приклад використання нерівності трикутника кілька порівняно нескладних геометричних завдань. Завдання 1. Доведіть, що у довільному чотирикутнику ABCD AB + CD < AC + BD.
. У трикутнику ABDкут ADBменше кута BADотже, BD > AB, або BC + CD
> AB. Але CD = ACотже, AC + BC > AB. Зауваження. Зверніть увагу, що, виходячи з формулювання теореми, слід записати відразу три нерівності: AB < AC + BC; AC< AB + BC; BC < AB + AC. Нерідко, записавши одну нерівність, про двох інших чомусь забувають. Пам'ятайте, що це може призвести до неприємних помилок. Нерівність трикутника може бути одним із простих критеріїв приналежності трьох точок однієї прямої. Три точки належать одній прямій тоді й лише тоді, коли в нерівності трикутника досягається рівність. Звичайно, рівність може досягатися лише в одній з трьох нерівностей (див. зауваження), оскільки одна з точок лежатиме чітко між двома іншими. Вправа. Доведіть, що у трикутнику кожна сторона більша за різницю двох інших сторін. Наведемо як приклад використання нерівності трикутника кілька порівняно нескладних геометричних завдань. Завдання 1. Доведіть, що у довільному чотирикутнику ABCD AB + CD < AC + BD.
Рішення
. Нехай O- Точка перетину діагоналей чотирикутника ABCD(Рис. 2). По нерівності трикутника:
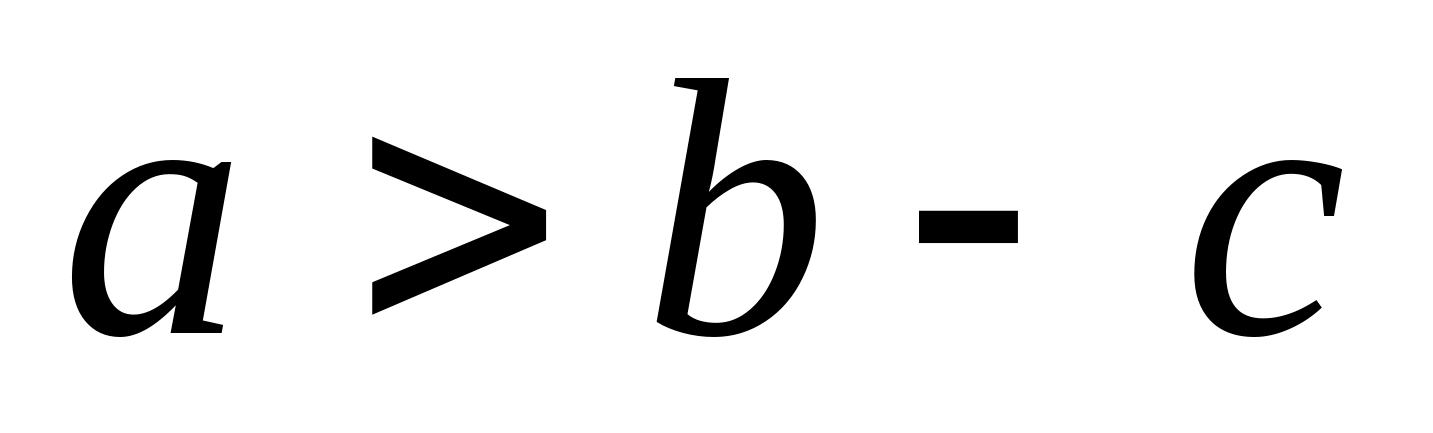 (Припускаємо, що
(Припускаємо, що 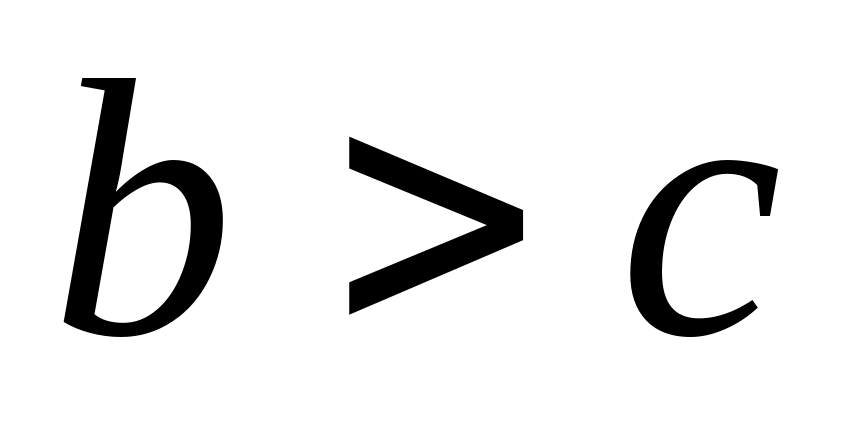 ). Тоді, звівши в квадрат обидві частини нерівності, отримаємо:
). Тоді, звівши в квадрат обидві частини нерівності, отримаємо: 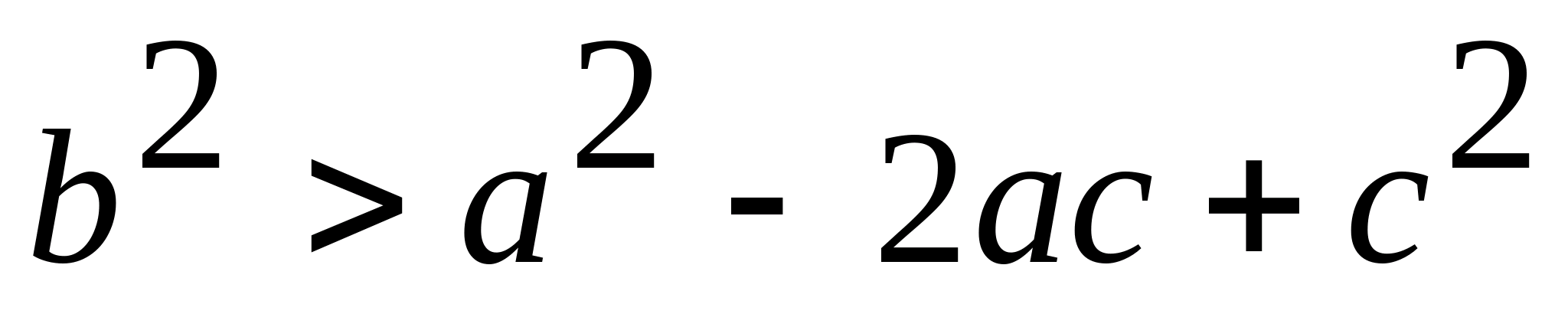 ;
;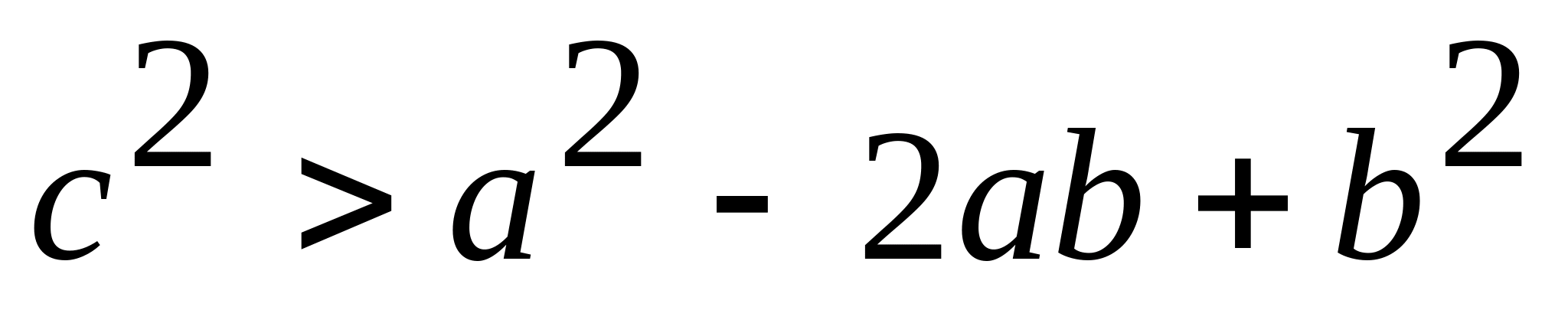 .
.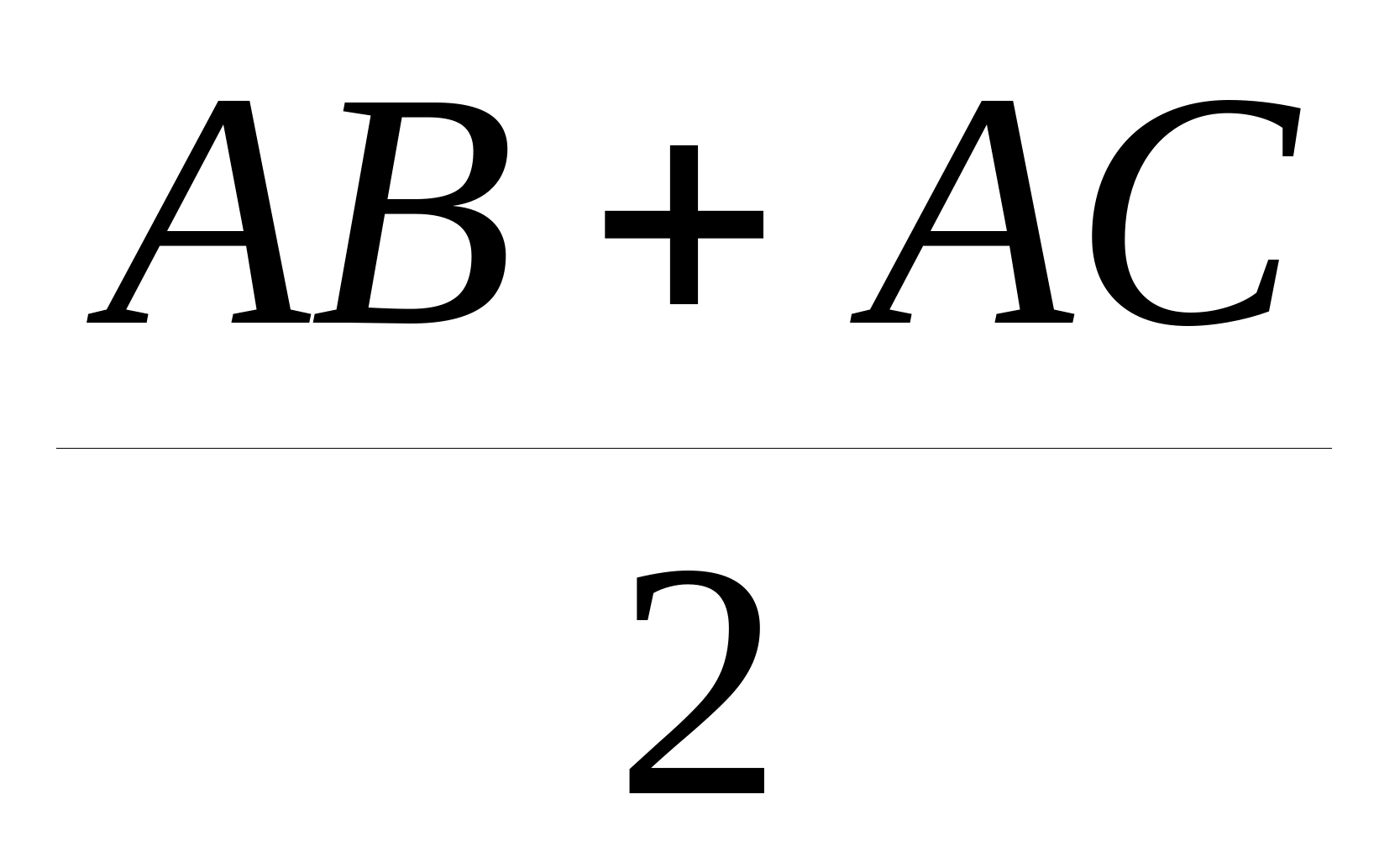 . Завдання 3. На площині дано квадрат ABCDі крапка O. Доведіть, що відстань від точки Oдо однієї з вершин квадрата не перевищує суми відстаней від Oдо трьох інших вершин квадрата. Рішення
. Складіть нерівності трикутника AC + OC > OAі OB + OD > BD. Так як AC = BD, то, скорочуючи, отримуємо необхідне. Завдання 4. Знайдіть усередині опуклого чотирикутника точку, що сума відстаней від неї до вершин мінімальна. Рішення
. Так як чотирикутник опуклий, його діагоналі перетинаються в точці Oусередині нього. Позначимо вершини чотирикутника через A, B, Cі D(по годинниковій стрілці). Тоді сума відстаней від Oдо вершин дорівнює сумі довжин діагоналей ACі BD. Але для будь-якої іншої точки Pмаємо, по-перше, що сума відстаней від Pдо вершин не менше AC + BD, а по-друге, або PA + PC > AC, або PB + PD > BD. Значить, ця сума дорівнює AC + BDтільки якщо Pзбігається з точкою O. Значить, точка O- Шукана. Нерівність трикутника успішно застосовується і в досить заплутаних текстових задачах. Що цікаво, у таких завданнях багато може залежати від того, наскільки вдало Ви збудуєте геометричну інтерпретацію. Завдання 5. У деякій країні розташовані 4 міста: A, B, Cі D. Два літаки одночасно вилетіли з міста A. Маршрут першого літака: A-B-D-C-A-D-B-C-A, А маршрут другого: A-B-C-D-A-B-C-D-A-B-C-D-A. Який із літаків раніше закінчить свій маршрут, якщо їхні швидкості однакові? Не бійтеся експериментувати! Якщо в задачі не задано конкретне розташування об'єктів, Ви маєте право малювати у своєму рішенні все, що не суперечить умові – адже воно Ваше. В тому числі, і міста в Задачі 5 Ви можете розставити як завгодно. Слід лише пам'ятати, що в деяких завданнях після розбору «нормального», загального випадку, необхідно розібрати і деякі «патологічні», окремі випадки. Наприклад, у Завданні 5 може знадобитися розгляд випадку, коли деякі три міста лежать на одній прямій – все залежить від того, яким є Ваше рішення для загального випадку. Розв'язання задачі 5
. Запишемо довжини маршрутів кожного літака у вигляді сум відстаней між містами. Довжина маршруту першого літака дорівнюватиме
. Завдання 3. На площині дано квадрат ABCDі крапка O. Доведіть, що відстань від точки Oдо однієї з вершин квадрата не перевищує суми відстаней від Oдо трьох інших вершин квадрата. Рішення
. Складіть нерівності трикутника AC + OC > OAі OB + OD > BD. Так як AC = BD, то, скорочуючи, отримуємо необхідне. Завдання 4. Знайдіть усередині опуклого чотирикутника точку, що сума відстаней від неї до вершин мінімальна. Рішення
. Так як чотирикутник опуклий, його діагоналі перетинаються в точці Oусередині нього. Позначимо вершини чотирикутника через A, B, Cі D(по годинниковій стрілці). Тоді сума відстаней від Oдо вершин дорівнює сумі довжин діагоналей ACі BD. Але для будь-якої іншої точки Pмаємо, по-перше, що сума відстаней від Pдо вершин не менше AC + BD, а по-друге, або PA + PC > AC, або PB + PD > BD. Значить, ця сума дорівнює AC + BDтільки якщо Pзбігається з точкою O. Значить, точка O- Шукана. Нерівність трикутника успішно застосовується і в досить заплутаних текстових задачах. Що цікаво, у таких завданнях багато може залежати від того, наскільки вдало Ви збудуєте геометричну інтерпретацію. Завдання 5. У деякій країні розташовані 4 міста: A, B, Cі D. Два літаки одночасно вилетіли з міста A. Маршрут першого літака: A-B-D-C-A-D-B-C-A, А маршрут другого: A-B-C-D-A-B-C-D-A-B-C-D-A. Який із літаків раніше закінчить свій маршрут, якщо їхні швидкості однакові? Не бійтеся експериментувати! Якщо в задачі не задано конкретне розташування об'єктів, Ви маєте право малювати у своєму рішенні все, що не суперечить умові – адже воно Ваше. В тому числі, і міста в Задачі 5 Ви можете розставити як завгодно. Слід лише пам'ятати, що в деяких завданнях після розбору «нормального», загального випадку, необхідно розібрати і деякі «патологічні», окремі випадки. Наприклад, у Завданні 5 може знадобитися розгляд випадку, коли деякі три міста лежать на одній прямій – все залежить від того, яким є Ваше рішення для загального випадку. Розв'язання задачі 5
. Запишемо довжини маршрутів кожного літака у вигляді сум відстаней між містами. Довжина маршруту першого літака дорівнюватимеФіхте Йоганн Готліб (1762-1814) - один з найвизначніших представників класичної німецької філософії. До книги увійшли відомі роботи: «Факти свідомості», «Призначення людини», «Науковчення» та інші книги
КнигаЖозеф Артур Гобіно. Досвід про нерівність людських рас
КнигаПентаграма одна із найважливіших магічних символів. Саме це слово походить від грецьких слів "pente", що означає п'ять, і "gramma" буква
Документ