आंकड़ों में फैलाव की गणना। अवशिष्ट फैलाव

समूहीकृत डेटा के लिए अवशिष्ट फैलाव- इंट्राग्रुप फैलाव का औसत:

जहाँ 2 j, j-वें समूह का अंतर-समूह प्रसरण है।

असमूहीकृत डेटा के लिए अवशिष्ट फैलावसन्निकटन सटीकता का एक उपाय है, अर्थात। मूल डेटा के लिए प्रतिगमन रेखा का सन्निकटन:
जहां y(t) प्रवृत्ति समीकरण के अनुसार पूर्वानुमान है; y t - गतिकी की प्रारंभिक श्रृंखला; n अंकों की संख्या है; p प्रतिगमन समीकरण (व्याख्यात्मक चर की संख्या) के गुणांकों की संख्या है।
इस उदाहरण में इसे कहा जाता है विचरण का निष्पक्ष अनुमान.

उदाहरण 1। टैरिफ श्रेणियों द्वारा एक संघ के तीन उद्यमों के श्रमिकों का वितरण निम्नलिखित आंकड़ों की विशेषता है:

श्रमिक वेतन श्रेणी	उद्यम में श्रमिकों की संख्या
श्रमिक वेतन श्रेणी	उद्यम 1	उद्यम 2	उद्यम 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

परिभाषित करना:
1. प्रत्येक उद्यम के लिए फैलाव (इंट्राग्रुप फैलाव);
2. इंट्राग्रुप फैलाव का औसत;
3. इंटरग्रुप फैलाव;
4. कुल विचरण.

समाधान।
समस्या को हल करने के लिए आगे बढ़ने से पहले, यह पता लगाना आवश्यक है कि कौन सी विशेषता प्रभावी है और कौन सी तथ्यात्मक है। विचाराधीन उदाहरण में, प्रभावी विशेषता "टैरिफ श्रेणी" है, और कारक विशेषता "उद्यम की संख्या (नाम)" है।
फिर हमारे पास तीन समूह (उद्यम) हैं जिनके लिए समूह औसत और इंट्राग्रुप भिन्नताओं की गणना करना आवश्यक है:

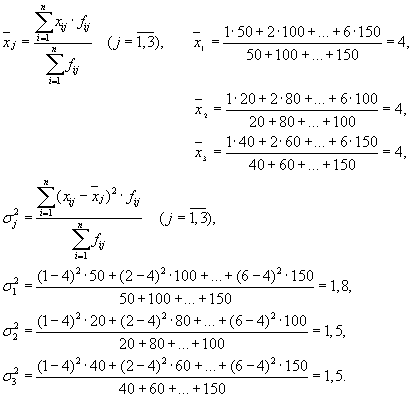
कंपनी	समूह औसत,	समूह के भीतर विचरण,
1	4	1,8

इंट्राग्रुप प्रसरणों का औसत ( अवशिष्ट फैलाव) सूत्र द्वारा परिकलित:

जहां आप गणना कर सकते हैं:

या:

फिर:
कुल फैलाव इसके बराबर होगा: s 2 \u003d 1.6 + 0 \u003d 1.6।
निम्नलिखित दो सूत्रों में से एक का उपयोग करके कुल विचरण की गणना भी की जा सकती है:

निर्णय लेते समय व्यावहारिक कार्यअक्सर किसी को ऐसी सुविधा से निपटना पड़ता है जो केवल दो वैकल्पिक मान लेता है। इस मामले में, वे किसी विशेषता के किसी विशेष मूल्य के वजन के बारे में बात नहीं कर रहे हैं, बल्कि कुल में इसके हिस्से के बारे में बात कर रहे हैं। यदि अध्ययन के तहत विशेषता वाली जनसंख्या इकाइयों के अनुपात को "द्वारा निरूपित किया जाता है" आर", और नहीं - के माध्यम से" क्यू”, तब फैलाव की गणना सूत्र द्वारा की जा सकती है:
एस 2 = पी × क्यू

उदाहरण # 2। ब्रिगेड के छह कर्मचारियों के आउटपुट के आंकड़ों के आधार पर, अंतरसमूह विचरण का निर्धारण करें और उनकी श्रम उत्पादकता पर कार्य शिफ्ट के प्रभाव का मूल्यांकन करें यदि कुल विचरण 12.2 है।

कार्यरत ब्रिगेड की संख्या	वर्किंग आउटपुट, पीसी।
कार्यरत ब्रिगेड की संख्या	पहली पाली में	दूसरी पाली में
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

समाधान. प्रारंभिक आंकड़े

एक्स	f1	f2	च 3	f4	f5	f6	कुल
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
कुल	31	33	37	37	40	38

फिर हमारे पास 6 समूह हैं जिनके लिए समूह माध्य और इंट्राग्रुप प्रसरणों की गणना करना आवश्यक है।
1. प्रत्येक समूह का औसत मान ज्ञात कीजिए.

2. प्रत्येक समूह का माध्य वर्ग ज्ञात कीजिए.

हम एक तालिका में गणना के परिणामों को संक्षेप में प्रस्तुत करते हैं:

समूह संख्या	समूह औसत	इंट्राग्रुप विचरण
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. इंट्राग्रुप विचरणसमूह में अंतर्निहित कारक को छोड़कर, सभी कारकों के प्रभाव में समूह के भीतर अध्ययन (परिणामी) विशेषता के परिवर्तन (भिन्नता) की विशेषता है:
हम सूत्र का उपयोग करके इंट्राग्रुप फैलाव के औसत की गणना करते हैं:

4. इंटरग्रुप विचरण समूह में अंतर्निहित एक कारक (तथ्यात्मक विशेषता) के प्रभाव में अध्ययन (परिणामस्वरूप) विशेषता के परिवर्तन (भिन्नता) की विशेषता है।
इंटरग्रुप फैलाव को इस प्रकार परिभाषित किया गया है:

कहाँ पे

फिर

कुल विचरणबिना किसी अपवाद के सभी कारकों (तथ्यात्मक लक्षण) के प्रभाव में अध्ययन (परिणामस्वरूप) विशेषता के परिवर्तन (भिन्नता) की विशेषता है। समस्या की स्थिति से, यह 12.2 के बराबर है।
प्रयोगसिद्ध सहसंबंध संबंध मापता है कि परिणामी विशेषता के कुल उतार-चढ़ाव का कितना हिस्सा अध्ययन किए गए कारक के कारण होता है। यह भाज्य विचरण का कुल विचरण का अनुपात है:

हम अनुभवजन्य सहसंबंध संबंध निर्धारित करते हैं:

सुविधाओं के बीच संबंध कमजोर या मजबूत (करीबी) हो सकते हैं। उनके मानदंड का मूल्यांकन चाडॉक पैमाने पर किया जाता है:
0.1 0.3 0.5 0.7 0.9 हमारे उदाहरण में, फीचर वाई फैक्टर एक्स के बीच संबंध कमजोर है
निर्धारण गुणांक।

आइए निर्धारण के गुणांक को परिभाषित करें:

इस प्रकार, 0.67% भिन्नता लक्षणों के बीच अंतर के कारण है, और 99.37% अन्य कारकों के कारण है।
निष्कर्ष: इस मामले में, श्रमिकों का उत्पादन एक विशेष पाली में काम पर निर्भर नहीं करता है, अर्थात। उनकी श्रम उत्पादकता पर कार्य शिफ्ट का प्रभाव महत्वपूर्ण नहीं है और अन्य कारकों के कारण है।

उदाहरण #3। औसत के आधार पर वेतनऔर श्रमिकों के दो समूहों के लिए इसके मान से वर्ग विचलन, प्रसरण जोड़ने के लिए नियम लागू करके कुल विचरण ज्ञात करें:

समाधान:
समूह के भीतर भिन्नताओं का औसत

इंटरग्रुप फैलाव को इस प्रकार परिभाषित किया गया है:

कुल विचरण होगा: 480 + 13824 = 14304

संभाव्यता सिद्धांत गणित की एक विशेष शाखा है जिसका अध्ययन केवल उच्च शिक्षण संस्थानों के छात्र ही करते हैं। क्या आपको गणना और सूत्र पसंद हैं? आप सामान्य वितरण, पहनावा एन्ट्रापी, गणितीय अपेक्षा और असतत विचरण के साथ परिचित होने की संभावनाओं से डरते नहीं हैं अनियमित चर? तब यह विषय आपके लिए बहुत रुचिकर होगा। आइए विज्ञान के इस खंड की कुछ सबसे महत्वपूर्ण बुनियादी अवधारणाओं से परिचित हों।

आइए मूल बातें याद रखें

यहां तक कि अगर आपको संभाव्यता सिद्धांत की सबसे सरल अवधारणाएं याद हैं, तो लेख के पहले पैराग्राफ की उपेक्षा न करें। तथ्य यह है कि बुनियादी बातों की स्पष्ट समझ के बिना, आप नीचे चर्चा किए गए सूत्रों के साथ काम करने में सक्षम नहीं होंगे।

तो, कुछ यादृच्छिक घटना है, कुछ प्रयोग है। किए गए कार्यों के परिणामस्वरूप, हम कई परिणाम प्राप्त कर सकते हैं - उनमें से कुछ अधिक सामान्य हैं, अन्य कम सामान्य हैं। एक घटना की संभावना एक प्रकार के वास्तव में प्राप्त परिणामों की संख्या का अनुपात है कुल गणनासंभव। केवल जानना क्लासिक परिभाषाइस अवधारणा का, आप अध्ययन शुरू कर सकते हैं गणितीय अपेक्षाऔर निरंतर यादृच्छिक चर का फैलाव।

औसत

स्कूल में वापस, गणित के पाठों में, आपने अंकगणितीय माध्य के साथ काम करना शुरू किया। इस अवधारणा का व्यापक रूप से संभाव्यता सिद्धांत में उपयोग किया जाता है, और इसलिए इसे अनदेखा नहीं किया जा सकता है। इस समय हमारे लिए मुख्य बात यह है कि हम गणितीय अपेक्षा और यादृच्छिक चर के विचरण के सूत्रों में इसका सामना करेंगे।

हमारे पास संख्याओं का एक क्रम है और हम अंकगणितीय माध्य ज्ञात करना चाहते हैं। हमारे लिए जो कुछ भी आवश्यक है वह सब कुछ उपलब्ध है और अनुक्रम में तत्वों की संख्या से विभाजित करना है। मान लीजिए हमारे पास 1 से 9 तक की संख्याएँ हैं। तत्वों का योग 45 होगा, और हम इस मान को 9 से विभाजित करेंगे। उत्तर: - 5।

फैलाव

वैज्ञानिक शब्दों में, विचरण अंकगणित माध्य से प्राप्त विशेषता मानों के विचलन का औसत वर्ग है। एक को बड़े लैटिन अक्षर D से दर्शाया जाता है। इसकी गणना करने के लिए क्या आवश्यक है? अनुक्रम के प्रत्येक तत्व के लिए, हम उपलब्ध संख्या और अंकगणितीय माध्य के बीच के अंतर की गणना करते हैं और इसे वर्ग करते हैं। जिस घटना पर हम विचार कर रहे हैं, उसके लिए उतने ही मूल्य होंगे जितने परिणाम हो सकते हैं। अगला, हम प्राप्त सभी चीजों को सारांशित करते हैं और अनुक्रम में तत्वों की संख्या से विभाजित करते हैं। यदि हमारे पास पांच संभावित परिणाम हैं, तो पांच से विभाजित करें।

विचरण में ऐसे गुण भी होते हैं जिन्हें समस्याओं को हल करते समय इसे लागू करने के लिए आपको याद रखने की आवश्यकता होती है। उदाहरण के लिए, यदि यादृच्छिक चर को X गुना बढ़ा दिया जाता है, तो विचरण वर्ग के X गुना बढ़ जाता है (अर्थात, X*X)। यह कभी भी शून्य से कम नहीं होता है और मूल्यों को एक समान मान ऊपर या नीचे स्थानांतरित करने पर निर्भर नहीं करता है। इसके अलावा, के लिए स्वतंत्र परीक्षणयोग का प्रसरण, प्रसरणों के योग के बराबर होता है।

अब हमें निश्चित रूप से एक असतत यादृच्छिक चर के प्रसरण और गणितीय अपेक्षा के उदाहरणों पर विचार करने की आवश्यकता है।

मान लीजिए कि हम 21 प्रयोग चलाते हैं और 7 अलग-अलग परिणाम प्राप्त करते हैं। हमने उनमें से प्रत्येक को क्रमशः 1,2,2,3,4,4 और 5 बार देखा। भिन्नता क्या होगी?

सबसे पहले, हम अंकगणितीय माध्य की गणना करते हैं: तत्वों का योग, निश्चित रूप से, 21 है। हम इसे 7 से विभाजित करते हैं, 3 प्राप्त करते हैं। अब हम मूल क्रम में प्रत्येक संख्या से 3 घटाते हैं, प्रत्येक मान को वर्ग करते हैं, और परिणाम एक साथ जोड़ते हैं . यह 12 निकला। अब हमारे लिए संख्या को तत्वों की संख्या से विभाजित करना बाकी है, और, ऐसा प्रतीत होता है, बस। लेकिन वहां एक जाल है! आइए इसकी चर्चा करते हैं।

प्रयोगों की संख्या पर निर्भरता

यह पता चला है कि विचरण की गणना करते समय, हर दो संख्याओं में से एक हो सकता है: या तो एन या एन -1। यहां एन अनुक्रम में किए गए प्रयोगों की संख्या या तत्वों की संख्या है (जो अनिवार्य रूप से वही बात है)। यह किस पर निर्भर करता है?

यदि परीक्षणों की संख्या सैकड़ों में मापी जाती है, तो हमें N को हर में रखना चाहिए। यदि इकाइयों में, तो N-1। वैज्ञानिकों ने सीमा को काफी प्रतीकात्मक रूप से खींचने का फैसला किया: आज यह संख्या 30 के साथ चलती है। यदि हमने 30 से कम प्रयोग किए हैं, तो हम राशि को एन -1 से विभाजित करेंगे, और यदि अधिक, तो एन द्वारा।

एक कार्य

आइए विचरण और अपेक्षा की समस्या को हल करने के अपने उदाहरण पर वापस जाएं। हमें मिला मध्यवर्ती संख्या 12, जिसे N या N-1 से विभाजित करना था। चूंकि हमने 21 प्रयोग किए, जो कि 30 से कम हैं, हम दूसरा विकल्प चुनेंगे। तो उत्तर है: विचरण 12/2 = 2 है।

अपेक्षित मूल्य

आइए दूसरी अवधारणा पर चलते हैं, जिस पर हमें इस लेख में विचार करना चाहिए। गणितीय अपेक्षा संगत संभावनाओं से गुणा किए गए सभी संभावित परिणामों को जोड़ने का परिणाम है। यह समझना महत्वपूर्ण है कि परिणामी मूल्य, साथ ही विचरण की गणना का परिणाम, पूरे कार्य के लिए केवल एक बार प्राप्त होता है, चाहे वह कितने भी परिणाम मानता हो।

गणितीय अपेक्षा सूत्र काफी सरल है: हम परिणाम लेते हैं, इसे इसकी संभावना से गुणा करते हैं, इसे दूसरे, तीसरे परिणाम आदि के लिए जोड़ते हैं। इस अवधारणा से संबंधित हर चीज की गणना करना आसान है। उदाहरण के लिए, गणितीय अपेक्षाओं का योग योग की गणितीय अपेक्षा के बराबर होता है। काम के लिए भी यही सच है। संभाव्यता सिद्धांत में प्रत्येक मात्रा ऐसे सरल कार्यों को करने की अनुमति नहीं देती है। आइए एक कार्य लें और उन दो अवधारणाओं के मूल्य की गणना करें जिनका हमने एक साथ अध्ययन किया है। इसके अलावा, हम सिद्धांत से विचलित थे - यह अभ्यास करने का समय है।

एक और उदाहरण

हमने 50 परीक्षण चलाए और 10 प्रकार के परिणाम प्राप्त किए - संख्या 0 से 9 - अलग-अलग प्रतिशत में दिखाई दे रहे हैं। ये क्रमशः हैं: 2%, 10%, 4%, 14%, 2%, 18%, 6%, 16%, 10%, 18%। याद रखें कि संभावनाएं प्राप्त करने के लिए, आपको प्रतिशत मानों को 100 से विभाजित करने की आवश्यकता है। इस प्रकार, हमें 0.02 मिलता है; 0.1 आदि आइए हम एक यादृच्छिक चर के प्रसरण और गणितीय अपेक्षा के लिए समस्या को हल करने का एक उदाहरण प्रस्तुत करते हैं।

हम प्राथमिक विद्यालय से याद किए गए सूत्र का उपयोग करके अंकगणितीय माध्य की गणना करते हैं: 50/10 = 5।

आइए अब संभावनाओं को "टुकड़ों में" परिणामों की संख्या में अनुवाद करें ताकि इसे गिनना अधिक सुविधाजनक हो सके। हमें 1, 5, 2, 7, 1, 9, 3, 8, 5 और 9 मिलते हैं। प्राप्त प्रत्येक मान से अंकगणितीय माध्य घटाएं, जिसके बाद हम प्राप्त परिणामों में से प्रत्येक का वर्ग करते हैं। उदाहरण के रूप में पहले तत्व के साथ इसे कैसे करें देखें: 1 - 5 = (-4)। आगे: (-4) * (-4) = 16. अन्य मूल्यों के लिए, ये ऑपरेशन स्वयं करें। अगर आपने सब कुछ ठीक किया, तो सब कुछ जोड़ने के बाद आपको 90 मिलते हैं।

आइए 90 को N से विभाजित करके विचरण और माध्य की गणना जारी रखें। हम N को क्यों चुनते हैं और N-1 को नहीं? यह सही है, क्योंकि किए गए प्रयोगों की संख्या 30 से अधिक है। तो: 90/10 = 9। हमें फैलाव मिला। अगर आपको कोई दूसरा नंबर मिलता है, तो निराश न हों। सबसे अधिक संभावना है, आपने गणना में एक सामान्य त्रुटि की है। आपने जो लिखा है उसे दोबारा जांचें, और निश्चित रूप से सब कुछ ठीक हो जाएगा।

अंत में, आइए गणितीय अपेक्षा सूत्र को याद करें। हम सभी गणना नहीं देंगे, हम केवल वही उत्तर लिखेंगे जिसके साथ आप सभी आवश्यक प्रक्रियाओं को पूरा करने के बाद जांच कर सकते हैं। अपेक्षित मान 5.48 होगा। हम केवल याद करते हैं कि पहले तत्वों के उदाहरण का उपयोग करके संचालन कैसे किया जाता है: 0 * 0.02 + 1 * 0.1 ... और इसी तरह। जैसा कि आप देख सकते हैं, हम परिणाम के मूल्य को इसकी संभावना से गुणा करते हैं।

विचलन

फैलाव और गणितीय अपेक्षा से संबंधित एक अन्य अवधारणा मानक विचलन है। यह या तो चिह्नित है लैटिन अक्षरों के साथएसडी, या ग्रीक लोअरकेस "सिग्मा"। यह अवधारणा दिखाती है कि कैसे, औसतन, मूल्य केंद्रीय विशेषता से विचलित होते हैं। इसका मान ज्ञात करने के लिए, आपको गणना करने की आवश्यकता है वर्गमूलफैलाव से।

यदि आप एक ग्राफ बनाते हैं सामान्य वितरणऔर सीधे उस पर वर्ग विचलन देखना चाहते हैं, यह कई चरणों में किया जा सकता है। छवि के आधे हिस्से को मोड (केंद्रीय मान) के बाईं या दाईं ओर ले जाएं, क्षैतिज अक्ष पर लंबवत खींचें ताकि परिणामी आंकड़ों के क्षेत्र बराबर हों। वितरण के मध्य और क्षैतिज अक्ष पर परिणामी प्रक्षेपण के बीच के खंड का मान मानक विचलन होगा।

सॉफ़्टवेयर

जैसा कि सूत्रों के विवरण और प्रस्तुत उदाहरणों से देखा जा सकता है, विचरण और गणितीय अपेक्षा की गणना अंकगणित की दृष्टि से सबसे आसान प्रक्रिया नहीं है। समय बर्बाद न करने के लिए, उच्चतर में उपयोग किए जाने वाले कार्यक्रम का उपयोग करना समझ में आता है शिक्षण संस्थानों- इसे "आर" कहा जाता है। इसमें ऐसे कार्य हैं जो आपको सांख्यिकी और संभाव्यता सिद्धांत से कई अवधारणाओं के मूल्यों की गणना करने की अनुमति देते हैं।

उदाहरण के लिए, आप मानों के वेक्टर को परिभाषित करते हैं। यह निम्नानुसार किया जाता है: वेक्टर<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.

आखिरकार

फैलाव और गणितीय अपेक्षाएं हैं जिनके बिना भविष्य में कुछ भी गणना करना मुश्किल है। विश्वविद्यालयों में व्याख्यान के मुख्य पाठ्यक्रम में, उन्हें विषय के अध्ययन के पहले महीनों में ही माना जाता है। इन सरल अवधारणाओं की समझ की कमी और उनकी गणना करने में असमर्थता के कारण ही कई छात्र तुरंत कार्यक्रम में पिछड़ने लगते हैं और बाद में सत्र के अंत में खराब ग्रेड प्राप्त करते हैं, जो उन्हें छात्रवृत्ति से वंचित करता है।

इस लेख में प्रस्तुत किए गए समान कार्यों को हल करते हुए, दिन में कम से कम एक सप्ताह में आधे घंटे का अभ्यास करें। फिर, किसी भी संभाव्यता सिद्धांत परीक्षण पर, आप बिना बाहरी युक्तियों और चीट शीट के उदाहरणों का सामना करेंगे।

फैलाव फैलाव का एक उपाय है जो डेटा मानों और माध्य के बीच सापेक्ष विचलन का वर्णन करता है। यह आँकड़ों में फैलाव का सबसे अधिक इस्तेमाल किया जाने वाला उपाय है, जिसकी गणना योग, वर्ग, माध्य से प्रत्येक डेटा मान के विचलन द्वारा की जाती है। प्रसरण की गणना के लिए सूत्र नीचे दिखाया गया है:

एस 2 - नमूना विचरण;

x cf नमूने का माध्य मान है;

एन — नमूना आकार (डेटा मानों की संख्या),

(x i - x cf) डेटा सेट के प्रत्येक मान के लिए माध्य मान से विचलन है।

सूत्र को बेहतर ढंग से समझने के लिए, आइए एक उदाहरण देखें। मुझे वास्तव में खाना बनाना पसंद नहीं है, इसलिए मैं इसे शायद ही कभी करता हूं। हालांकि, भूख से नहीं मरने के लिए, समय-समय पर मुझे अपने शरीर को प्रोटीन, वसा और कार्बोहाइड्रेट से संतृप्त करने की योजना को लागू करने के लिए स्टोव पर जाना पड़ता है। नीचे दिया गया डेटा दिखाता है कि रेनाट हर महीने कितनी बार खाना बनाती है:

विचरण की गणना में पहला कदम नमूना माध्य निर्धारित करना है, जो हमारे उदाहरण में महीने में 7.8 गुना है। शेष गणनाओं को निम्न तालिका की सहायता से सुगम बनाया जा सकता है।

विचरण की गणना का अंतिम चरण इस तरह दिखता है:

जो लोग एक बार में सभी गणना करना पसंद करते हैं, उनके लिए समीकरण इस तरह दिखेगा:

कच्ची गिनती विधि का उपयोग करना (खाना पकाने का उदाहरण)

विचरण की गणना करने का एक अधिक कुशल तरीका है, जिसे "कच्ची गिनती" विधि के रूप में जाना जाता है। हालांकि पहली नज़र में समीकरण काफी बोझिल लग सकता है, वास्तव में यह इतना डरावना नहीं है। आप इसे सत्यापित कर सकते हैं, और फिर तय कर सकते हैं कि आपको कौन सा तरीका सबसे अच्छा लगता है।

चुकता करने के बाद प्रत्येक डेटा मान का योग है,

सभी डेटा मानों के योग का वर्ग है।

अभी अपना दिमाग मत खोइए। आइए इसे एक तालिका के रूप में रखें, और फिर आप देखेंगे कि पिछले उदाहरण की तुलना में यहां कम गणनाएं हैं।

जैसा कि आप देख सकते हैं, परिणाम वही है जो पिछली विधि का उपयोग करते समय होता है। इस पद्धति के लाभ स्पष्ट हो जाते हैं क्योंकि नमूना आकार (एन) बढ़ता है।

एक्सेल में विचरण की गणना करना

जैसा कि आप शायद पहले ही अनुमान लगा चुके हैं, एक्सेल में एक सूत्र है जो आपको विचरण की गणना करने की अनुमति देता है। इसके अलावा, एक्सेल 2010 से, आप फैलाव सूत्र की 4 किस्में पा सकते हैं:

1) VAR.V - नमूने का प्रसरण लौटाता है। बूलियन मान और पाठ पर ध्यान नहीं दिया जाता है।

2) VAR.G - जनसंख्या विचरण लौटाता है। बूलियन मान और पाठ पर ध्यान नहीं दिया जाता है।

3) VASP - बूलियन और टेक्स्ट मानों को ध्यान में रखते हुए नमूना विचरण लौटाता है।

4) VARP - तार्किक और पाठ मानों को ध्यान में रखते हुए जनसंख्या का विचरण लौटाता है।

सबसे पहले, आइए एक नमूने और एक जनसंख्या के बीच के अंतर को देखें। वर्णनात्मक आँकड़ों का उद्देश्य डेटा को इस तरह से सारांशित करना या प्रदर्शित करना है ताकि जल्दी से एक बड़ी तस्वीर मिल सके, इसलिए बोलने के लिए, एक सिंहावलोकन। सांख्यिकीय अनुमान आपको इस जनसंख्या के डेटा के नमूने के आधार पर जनसंख्या के बारे में अनुमान लगाने की अनुमति देता है। जनसंख्या उन सभी संभावित परिणामों या मापों का प्रतिनिधित्व करती है जो हमारे लिए रुचिकर हैं। एक नमूना जनसंख्या का एक सबसेट है।

उदाहरण के लिए, हम रूसी विश्वविद्यालयों में से एक के छात्रों के समूह की समग्रता में रुचि रखते हैं और हमें समूह के औसत स्कोर को निर्धारित करने की आवश्यकता है। हम छात्रों के औसत प्रदर्शन की गणना कर सकते हैं, और फिर परिणामी आंकड़ा एक पैरामीटर होगा, क्योंकि पूरी आबादी हमारी गणना में शामिल होगी। हालांकि, अगर हम अपने देश के सभी छात्रों के जीपीए की गणना करना चाहते हैं, तो यह समूह हमारा नमूना होगा।

नमूना और जनसंख्या के बीच विचरण की गणना के लिए सूत्र में अंतर हर में है। जहां नमूने के लिए यह (n-1) के बराबर होगा, और सामान्य जनसंख्या के लिए केवल n।

अब आइए अंत के साथ विचरण की गणना के कार्यों से निपटें लेकिन,जिसके विवरण में यह कहा गया है कि गणना पाठ और तार्किक मूल्यों को ध्यान में रखती है। इस मामले में, एक विशिष्ट डेटा सेट के विचरण की गणना करते समय जहां गैर-संख्यात्मक मान होते हैं, एक्सेल टेक्स्ट और झूठे बूलियन को 0 के रूप में और सच्चे बूलियन को 1 के रूप में व्याख्या करेगा।

इसलिए, यदि आपके पास डेटा की एक सरणी है, तो ऊपर सूचीबद्ध एक्सेल फ़ंक्शन में से किसी एक का उपयोग करके इसके विचरण की गणना करना मुश्किल नहीं होगा।

फैलाव एक यादृच्छिक चर का (बिखरना) एक यादृच्छिक चर के वर्ग विचलन की गणितीय अपेक्षा से इसकी गणितीय अपेक्षा है:

विचरण की गणना करने के लिए, आप थोड़ा संशोधित सूत्र का उपयोग कर सकते हैं

इसलिये एम (एक्स), 2 और
स्थिर मूल्य हैं। इस तरह,

4.2.2 फैलाव गुण

संपत्ति 1.एक स्थिर मान का परिक्षेपण शून्य होता है। दरअसल, परिभाषा के अनुसार

संपत्ति 2.अचर गुणनखंड को परिक्षेपण चिह्न से वर्ग करके निकाला जा सकता है।

सबूत

केंद्रित एक यादृच्छिक चर अपनी गणितीय अपेक्षा से एक यादृच्छिक चर का विचलन है:

केंद्रित मूल्य में दो गुण होते हैं जो परिवर्तन के लिए सुविधाजनक होते हैं:

संपत्ति 3.यदि यादृच्छिक चर X और यूस्वतंत्र, तो

सबूत. निरूपित
. फिर।

दूसरे कार्यकाल में, यादृच्छिक चर की स्वतंत्रता और केंद्रित यादृच्छिक चर के गुणों के कारण

उदाहरण 4.5।यदि एक एकतथा बीस्थिर हैं, तो D (एकएक्स+बी)= डी(एकएक्स)+डी(बी)=
.

4.2.3. मानक विचलन

फैलाव, एक यादृच्छिक चर के प्रसार की विशेषता के रूप में, एक खामी है। यदि, उदाहरण के लिए, एक्स- माप त्रुटि का आयाम है मिमी, तो विचरण का आयाम है
. इसलिए, अक्सर एक और स्कैटर विशेषता का उपयोग करना पसंद किया जाता है - मानक विचलन , जो प्रसरण के वर्गमूल के बराबर है

मानक विचलन का आयाम यादृच्छिक चर के समान ही होता है।

उदाहरण 4.6।स्वतंत्र परीक्षणों की योजना में किसी घटना के घटित होने की संख्या का प्रसरण

प्रस्तुत एनस्वतंत्र परीक्षण और प्रत्येक परीक्षण में होने वाली घटना की संभावना है आर. हम पहले की तरह घटना के घटित होने की संख्या व्यक्त करते हैं एक्सव्यक्तिगत प्रयोगों में घटना के घटित होने की संख्या के माध्यम से:

चूंकि प्रयोग स्वतंत्र हैं, इसलिए प्रयोगों से जुड़े यादृच्छिक चर स्वतंत्र। और स्वतंत्रता के आधार पर अपने पास

लेकिन प्रत्येक यादृच्छिक चर का एक वितरण नियम होता है (उदाहरण 3.2)

तथा
(उदाहरण 4.4)। इसलिए, भिन्नता की परिभाषा के अनुसार:

कहाँ पे क्यू=1- पी.

नतीजतन, हमारे पास है
,

में किसी घटना के घटित होने की संख्या का मानक विचलन एनस्वतंत्र प्रयोग
.

4.3. यादृच्छिक चर के क्षण

पहले से ही विचार किए गए लोगों के अलावा, यादृच्छिक चर में कई अन्य संख्यात्मक विशेषताएं हैं।

प्रारंभिक क्षण क एक्स (
) को गणितीय अपेक्षा कहा जाता है कइस यादृच्छिक चर की शक्ति।

केंद्रीय क्षण क-वें क्रम यादृच्छिक चर एक्सउम्मीद कहा जाता है कसंबंधित केंद्रित मात्रा की th शक्ति।

यह देखना आसान है कि पहले क्रम का केंद्रीय क्षण हमेशा शून्य के बराबर होता है, दूसरे क्रम का केंद्रीय क्षण फैलाव के बराबर होता है, क्योंकि .

तीसरे क्रम का केंद्रीय क्षण एक यादृच्छिक चर के वितरण की विषमता का एक विचार देता है। दूसरे की तुलना में उच्च क्रम के क्षण अपेक्षाकृत कम ही उपयोग किए जाते हैं, इसलिए हम खुद को केवल उनकी अवधारणाओं तक ही सीमित रखेंगे।

4.4. वितरण कानून खोजने के उदाहरण

यादृच्छिक चरों के वितरण नियमों और उनकी संख्यात्मक विशेषताओं को खोजने के उदाहरणों पर विचार करें।

उदाहरण 4.7।

लक्ष्य पर तीन शॉट्स के साथ लक्ष्य पर हिट की संख्या के लिए वितरण कानून संकलित करें, यदि प्रत्येक शॉट के साथ मारने की संभावना 0.4 है। अभिन्न कार्य खोजें एफ(एक्स)असतत यादृच्छिक चर के परिणामी वितरण के लिए एक्सऔर उसका आलेख खींचिए। गणितीय अपेक्षा खोजें एम(एक्स) , फैलाव डी(एक्स) और मानक विचलन
(एक्स) अनियमित चर एक्स.

समाधान

1) असतत यादृच्छिक चर एक्स- तीन शॉट्स के साथ लक्ष्य पर हिट की संख्या - चार मान ले सकते हैं: 0, 1, 2, 3 . संभावना है कि वह उनमें से प्रत्येक को स्वीकार करेगी, हम बर्नौली सूत्र द्वारा पाते हैं: एन=3,पी=0,4,क्यू=1- पी=0.6 और एम=0, 1, 2, 3:

संभावित मूल्यों की संभावनाएं प्राप्त करें एक्स:;

आइए हम एक यादृच्छिक चर के वितरण के वांछित नियम की रचना करें एक्स:

नियंत्रण: 0.216+0.432+0.288+0.064=1.

आइए प्राप्त यादृच्छिक चर के वितरण बहुभुज का निर्माण करें एक्स. ऐसा करने के लिए, एक आयताकार समन्वय प्रणाली में, बिंदुओं (0; 0.216), (1; 0.432), (2; 0.288), (3; 0.064) को चिह्नित करें। आइए इन बिंदुओं को रेखाखंडों से जोड़ते हैं, परिणामी टूटी हुई रेखा वांछित वितरण बहुभुज है (चित्र 4.1)।

2) यदि x 0, तब एफ(एक्स)= 0। दरअसल, शून्य से कम के मान के लिए, मान एक्सस्वीकार नहीं करता है। इसलिए, सभी के लिए एक्स0 , परिभाषा का उपयोग करते हुए एफ(एक्स), हम पाते हैं एफ(एक्स)=पी(एक्स< एक्स) = 0 (एक असंभव घटना की संभावना के रूप में)।

अगर 0 , फिर एफ(एक्स) =0.216। दरअसल, इस मामले में एफ(एक्स)=पी(एक्स< एक्स) = =पी(- < एक्स 0)+ पी(0< एक्स< एक्स) =0,216+0=0,216.

उदाहरण के लिए, यदि हम लेते हैं, एक्स=0.2, तब एफ(0,2)=पी(एक्स<0,2) . लेकिन किसी घटना की प्रायिकता एक्स<0,2 равна 0,216, так как случайная величинаएक्सकेवल एक मामले में 0.2 से कम मान लेता है, अर्थात् 0 0.216 की संभावना के साथ।

अगर 1 , फिर

सचमुच, एक्स 0.216 की प्रायिकता के साथ मान 0 और 0.432 की प्रायिकता के साथ मान 1 ले सकते हैं; इसलिए, इन मूल्यों में से एक, चाहे कोई भी हो, एक्स 0.648 की संभावना के साथ (असंगत घटनाओं की संभावनाओं को जोड़ने के प्रमेय के अनुसार) स्वीकार कर सकते हैं।

अगर 2 , फिर, इसी तरह बहस करते हुए, हम प्राप्त करते हैं एफ(एक्स)=0.216+0.432 + + 0.288=0.936। दरअसल, चलो, उदाहरण के लिए, एक्स=3. फिर एफ(3)=पी(एक्स<3) एक घटना की संभावना व्यक्त करता है एक्स<3 – стрелок сделает меньше трех попаданий, т.е. ноль, один или два. Применяя теорему сложения вероятностей, получим указанное значение функцииएफ(एक्स).

यदि एक एक्स>3, तो एफ(एक्स)=0.216+0.432+0.288+0.064=1. दरअसल, घटना एक्स
विश्वसनीय है और इसकी प्रायिकता एक के बराबर है, और एक्स>3 - असंभव। मान लें कि

एफ(एक्स)=पी(एक्स< एक्स) =पी(एक्स 3) + पी(3< एक्स< एक्स) , हमें संकेतित परिणाम मिलता है।

तो, यादृच्छिक चर X का वांछित अभिन्न वितरण फलन प्राप्त होता है:

एफ(एक्स) =

जिसका ग्राफ अंजीर में दिखाया गया है। 4.2.

3) एक असतत यादृच्छिक चर की गणितीय अपेक्षा सभी संभावित मूल्यों के उत्पादों के योग के बराबर होती है एक्सउनकी संभावनाओं पर:

एम (एक्स)=0=1,2.

यानी औसतन तीन शॉट के साथ लक्ष्य पर एक हिट होती है।

विचरण की गणना विचरण की परिभाषा से की जा सकती है डी(एक्स)= एम(एक्स- एम(एक्स)) या सूत्र का उपयोग करें डी(एक्स)= एम(एक्स
, जो लक्ष्य को तेजी से ले जाता है।

आइए एक यादृच्छिक चर के वितरण का नियम लिखें एक्स :

के लिए गणितीय अपेक्षा का पता लगाएं एक्स:

एम (एक्स ) = 04
= 2,16.

आइए वांछित विचरण की गणना करें:

डी(एक्स) = एम(एक्स ) – (एम(एक्स)) = 2,16 – (1,2)= 0,72.

माध्य वर्ग विचलन सूत्र द्वारा ज्ञात किया जाता है

(एक्स) =
= 0,848.

मध्यान्तर ( एम- ; एम+ ) = (1.2-0.85; 1.2+0.85) = (0.35; 2.05) - यादृच्छिक चर के सबसे संभावित मूल्यों का अंतराल एक्स, मान 1 और 2 इसमें आते हैं।

उदाहरण 4.8।

एक सतत यादृच्छिक चर का विभेदक वितरण फलन (घनत्व फलन) दिया गया है एक्स:

एफ(एक्स) =

1) एक स्थिर पैरामीटर को परिभाषित करें एक.

2) अभिन्न फलन ज्ञात कीजिए एफ(एक्स) .

3) प्लॉट फंक्शन ग्राफ एफ(एक्स) तथा एफ(एक्स) .

4) प्रायिकता के दो तरीके खोजें पी (0.5< एक्स 1,5) तथा पी(1,5< एक्स<3,5) .

5). गणितीय अपेक्षा खोजें एम (एक्स), फैलाव डी(एक्स)और मानक विचलन
अनियमित चर एक्स.

समाधान

1) संपत्ति द्वारा विभेदक कार्य एफ(एक्स) शर्त को पूरा करना चाहिए
.

आइए हम दिए गए फलन के लिए इस अनुचित समाकलन की गणना करें एफ(एक्स) :

इस परिणाम को समानता के बाईं ओर रखने पर, हम पाते हैं कि एक= 1। के लिए हालत में एफ(एक्स) पैरामीटर बदलें एकएक पर:

2) खोजने के लिए एफ(एक्स) सूत्र का प्रयोग करें

यदि x
, फिर
, फलस्वरूप,

अगर 1
फिर

अगर x>2 तो

तो, वांछित अभिन्न कार्य एफ(एक्स) की तरह लगता है:

3) आइए कार्यों के रेखांकन बनाएं एफ(एक्स) तथा एफ(एक्स) (अंजीर। 4.3 और 4.4)।

4) किसी दिए गए अंतराल में एक यादृच्छिक चर के टकराने की प्रायिकता (एक,बी) सूत्र द्वारा गणना
, यदि फ़ंक्शन ज्ञात है एफ(एक्स), और सूत्र के अनुसार पी(एक < एक्स < बी) = एफ(बी) – एफ(एक), यदि फ़ंक्शन ज्ञात है एफ(एक्स).

हमे पता करने दें
दो सूत्रों का उपयोग करके और परिणामों की तुलना करें। शर्त के अनुसार ए = 0.5;बी=1,5; समारोह एफ(एक्स) पैराग्राफ 1 में निर्दिष्ट)। इसलिए, सूत्र के अनुसार वांछित संभावना है:

समान संभावना की गणना सूत्र द्वारा की जा सकती है b) पैराग्राफ 2 में प्राप्त वेतन वृद्धि के माध्यम से)। अभिन्न कार्य एफ(एक्स) इस अंतराल पर:

इसलिये एफ(0,5)=0.

इसी तरह, हम पाते हैं

इसलिये एफ(3,5)=1.

5) गणितीय अपेक्षा का पता लगाने के लिए एम (एक्स)सूत्र का प्रयोग करें
समारोह एफ(एक्स) पैराग्राफ 1 के निर्णय में दिया गया है, यह अंतराल के बाहर शून्य के बराबर है (1,2]: