एक त्रिभुज की भुजाओं की असमानता पर प्रमेय। असमानित त्रिकोण। संपूर्ण पाठ - ज्ञान हाइपरमार्केट
- असमानित त्रिकोण।
पाठ मकसद
- त्रिभुजों से संबंधित नई परिभाषाओं और प्रमेयों से परिचित हों।
- समस्याओं को हल करने में आकृतियों के गुणों को लागू करना सीखें।
- विकास करना - छात्रों का ध्यान, दृढ़ता, दृढ़ता विकसित करना, तार्किक सोच, गणितीय भाषण।
- शैक्षिक - एक पाठ के माध्यम से, एक-दूसरे के प्रति चौकस रवैया विकसित करना, साथियों को सुनने की क्षमता पैदा करना, आपसी सहायता, स्वतंत्रता।
पाठ मकसद
- छात्रों की समस्याओं को हल करने की क्षमता की जाँच करें।
शिक्षण योजना
- गणित के इतिहास से।
- पहले सीखी गई सामग्री की पुनरावृत्ति।
- नई सामग्री सीखना।
- समस्या समाधान का एक उदाहरण।
- स्व-जांच के लिए कार्य।
गणित के इतिहास से
यह बेबीलोनियन ज्यामिति में एक सम्मानजनक स्थान रखता है, इसका उल्लेख अक्सर अहम्स के पपीरस में मिलता है।
कर्ण शब्द ग्रीक हाइपोटिन्सा से आया है, जिसका अर्थ है किसी चीज के नीचे खींचना, कसना। यह शब्द प्राचीन मिस्र के वीणाओं की छवि से उत्पन्न हुआ है, जिस पर दो परस्पर लंबवत स्टैंडों के सिरों पर तार खिंचे हुए थे।
कैथेटस शब्द ग्रीक शब्द "कैथेटोस" से आया है, जिसका अर्थ है एक साहुल रेखा, लंबवत। मध्य युग में, कैटेट शब्द का अर्थ ऊंचाई था सही त्रिकोण, जबकि इसके अन्य पक्षों को क्रमशः कर्ण, आधार कहा जाता था। 17वीं शताब्दी में, आधुनिक अर्थों में केट शब्द का प्रयोग शुरू हुआ और 18वीं शताब्दी से व्यापक रूप से वितरित किया जाने लगा।
यूक्लिड अभिव्यक्तियों का उपयोग करता है:
"पक्ष जो एक समकोण बनाते हैं" - पैरों के लिए;
"वह पक्ष जो समकोण को घटाता है" - कर्ण के लिए।
शुरू करने के लिए, त्रिकोण असमानता के विषय में, मैं याद करने का प्रस्ताव करता हूं जो पहले से ही पारित हो चुका है, स्मृति में ताज़ा करने के लिए जो पहले से ही अध्ययन किया जा चुका है, अर्थात् त्रिभुजों की समानता के संकेत। आइए त्रिभुजों की समानता के चिन्हों की ऐतिहासिक पृष्ठभूमि से शुरुआत करें। विषय को पूरी तरह से समझने के लिए, क्या और कैसे, कब और किसके द्वारा लिखा और सिद्ध किया गया।
त्रिभुजों की समानता के संकेतों पर ऐतिहासिक पृष्ठभूमि
यदि हम इतिहास की ओर मुड़ें, तो ज्यामिति पर पहली पाठ्यपुस्तक - यूक्लिड के "तत्व" में हम निम्नलिखित परिभाषा पा सकते हैं: "आंकड़े जो एक दूसरे के साथ जुड़ते हैं वे एक दूसरे के बराबर होते हैं ..."। दो हजार से अधिक वर्ष बीत चुके हैं, और परिभाषा नहीं बदली है। आकृतियों की समानता की यह परिभाषा त्रिभुजों पर भी लागू की जा सकती है।
- तो, किन त्रिभुजों को समान कहा जाता है?
- लेकिन क्या हम हमेशा त्रिभुजों को वास्तव में संयोजित करने का प्रबंधन करते हैं?
- वास्तव में, कभी-कभी त्रिभुजों को जोड़ना संभव नहीं होता है। क्या करें? एक त्रिभुज के केवल तीन तत्वों की दूसरे त्रिभुज के तीन तत्वों से तुलना करना पर्याप्त है। यह वह जगह है जहां त्रिकोण की समानता के संकेत हमारी सहायता के लिए आएंगे, वे हमें बताएंगे कि किन तत्वों की तुलना करने की आवश्यकता है। त्रिभुजों की समता का चिन्ह क्या होता है और कितने चिन्ह होते हैं? कुछ शर्तें जिनके तहत दो दिए गए त्रिभुज बराबर होते हैं, त्रिभुज समानता मानदंड कहलाते हैं। हम कह सकते हैं कि एक चिन्ह एक चिन्ह है जिसके द्वारा आप आकृतियों के कुछ गुणों का पता लगा सकते हैं।
वीडियो पाठ "त्रिकोण असमानता" त्रिभुज असमानता प्रमेय की सामग्री और प्रमाण को प्रकट करता है। इस वीडियो पाठ का उद्देश्य प्रमेय और उसके उपफलों को याद रखना आसान बनाना है, इसे सिद्ध करते समय तर्क के पाठ्यक्रम को समझना और याद रखना है।
सामग्री के दृश्य का उच्च स्तर, आवाज संगत इस मैनुअल को पाठ के एक स्वतंत्र भाग के रूप में उपयोग करना संभव बनाता है, शिक्षण की गुणवत्ता में सुधार करने के लिए शिक्षक के समय को मुक्त करता है, छात्रों के साथ व्यक्तिगत कार्य को मजबूत करता है।
वीडियो ट्यूटोरियल विषय का परिचय और त्रिभुज असमानता प्रमेय बताते हुए शुरू होता है। प्रमेय के कथन को याद रखने के लिए, इसे प्रदर्शित किया जाता है और रंग में हाइलाइट किया जाता है। यह प्रमेय कहता है कि त्रिभुज की कोई भी भुजा उसकी अन्य दो भुजाओं के योग से कम होती है। स्क्रीन पर प्रमेय के पाठ के तहत दिखाए गए त्रिभुज Δ के उदाहरण पर विचार करने के लिए अभिकथन का प्रमाण प्रस्तावित है।
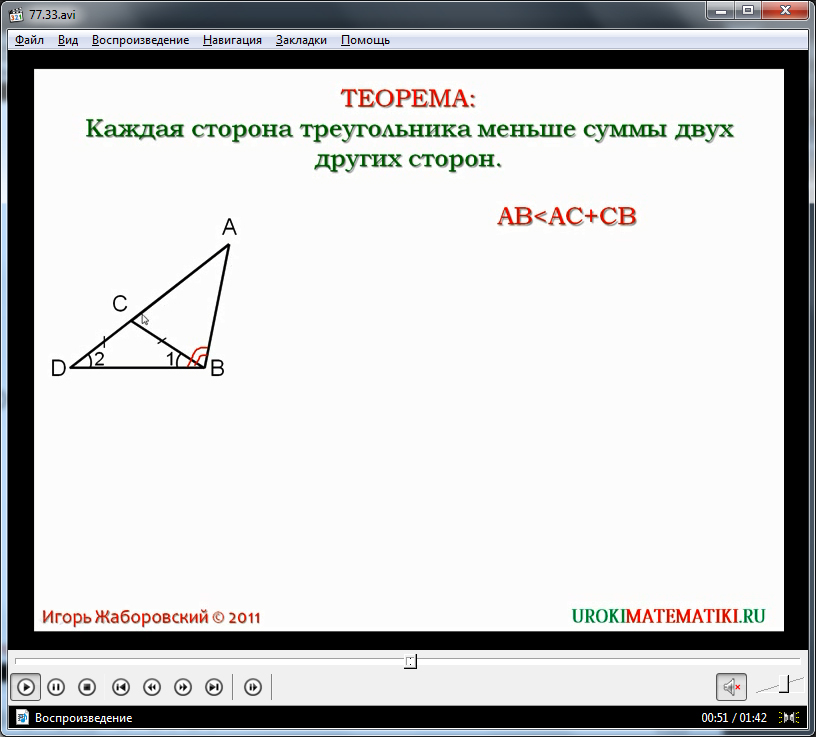
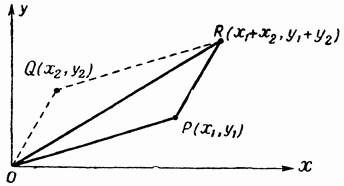
यह स्पष्ट किया जाता है कि प्रमेय को सिद्ध करने के लिए, यह पुष्टि करना आवश्यक है कि भुजा AB भुजा AC और CB के योग से कम है। यह कथन स्क्रीन पर व्यंजक AB . द्वारा दर्शाया गया है इस प्रमेय में महारत हासिल करने के बाद, हम इसके परिणाम पर विचार कर सकते हैं, जिसमें कहा गया है कि किन्हीं तीन बिंदुओं A, B, C के लिए जो एक ही रेखा से संबंधित नहीं हैं, निम्नलिखित असमानताएँ सत्य हैं: AB वीडियो पाठ "त्रिकोण असमानता" का उपयोग शिक्षक द्वारा ज्यामिति पाठ में एक दृश्य सहायता के रूप में या पाठ के भाग के रूप में किया जा सकता है, बजाय इसके कि शिक्षक किसी नए विषय को समझाए। एक विस्तृत, समझने योग्य स्पष्टीकरण शिक्षक की जगह लेगा जब छात्र स्वयं विषय का अध्ययन करेगा, और दूरस्थ शिक्षा में विषय को समझाने में भी मदद करेगा। रुसानिव लिसेयुम का गणितीय वृत्त असमानित त्रिकोण त्रिभुज असमानता सबसे महत्वपूर्ण ज्यामितीय तथ्यों में से एक है। दूरी के सहज गुणों में से एक का प्रतिनिधित्व करते हुए, यह अक्सर कठिन ज्यामितीय और शब्द समस्याओं को हल करने में मदद करता है। त्रिभुज असमानता की मदद से, बोझिल ज्यामितीय समस्याओं में किसी भी तत्व के स्थान के लिए कुछ संभावित विकल्पों को निकालना संभव लगता है। अक्सर यह त्रिभुज की सख्त असमानता (अर्थात् उसमें समानता की उपलब्धि) की गैर-पूर्ति है जो यह दावा करने का कारण देती है कि तीन बिंदु एक सीधी रेखा से संबंधित हैं। इस प्रकार, त्रिभुज असमानता सहज और स्पष्ट दोनों है, लेकिन बहुत बार गंभीर गणितीय समस्याओं को हल करने में एक शक्तिशाली उपकरण बन जाता है। असमानताओं के बारे में कुछ शब्द गणित में असमानताप्रश्न में दो वस्तुओं के सापेक्ष परिमाण या क्रम के बारे में एक बयान है, या वे बस समान नहीं हैं। अध्ययन की वस्तु के रूप में शास्त्रीय असमानता को आदेश संबंध का एक विशेष मामला भी माना जा सकता है। अंतर करना कठोरतथा गैर सख्तअसमानताएं या, संबंधों की भाषा पर स्विच करते हुए, एक सख्त असमानता को वास्तविक संख्याओं के सेट पर सख्त आदेश का संबंध माना जा सकता है (अर्थात, एक ऐसा संबंध जिसमें एंटीरफ्लेक्सिविटी, एंटीसिमेट्री और ट्रांज़िटिविटी के गुण होते हैं)। यदि हम एक गैर-सख्त असमानता के बारे में बात कर रहे हैं, तो हम इसके बारे में एक ही सेट पर गैर-सख्त आदेश के संबंध के रूप में बात कर सकते हैं (यानी, एंटी-रिफ्लेक्सिविटी के बजाय रिफ्लेक्सिविटी पर विचार करें)। याद कीजिए कि हमने पहले ही व्याख्यान 7 में संबंधों को एक गणितीय वस्तु के रूप में और उनके गुणों का उल्लेख किया था (विभाज्यता संबंध के गुणों पर विचार किया गया था)। हमें भविष्य में उनका और अधिक विस्तार से अध्ययन करना होगा, क्योंकि वे कई प्राथमिक गणितीय अवधारणाओं को सफलतापूर्वक व्यवस्थित और सामान्य करते हैं। अब हम इनमें से प्रत्येक प्रकार की असमानताओं के कई उदाहरण देते हैं। कठोरअसमानताओं को ऐसी असमानताएँ कहा जाता है: असमानित त्रिकोण एओ + ओबी > अब; सीओ + आयुध डिपो > सीडी. राशि पर विचार करें एसी + बीडी: एसी + बीडी = (एओ + ओसी) + (बो + आयुध डिपो) = = (एओ + बो) + (ओसी + आयुध डिपो) > अब + सीडी. इसी तरह: सभी तीन असमानताओं को जोड़कर, हम आवश्यक एक प्राप्त करते हैं। एक व्यायाम. सिद्ध कीजिए कि माध्यिका पूर्वाह्नएक मनमाना त्रिभुज में एबीसीलंबाई से छोटा दूसरा विमान उड़ान भरेगा दूरी पहले विमान द्वारा तय की गई दूरी और दूसरे विमान द्वारा तय की गई दूरी के बीच के अंतर पर विचार करें। आइए हम साबित करें कि, बिंदुओं के स्थान की परवाह किए बिना ए, बी, सी, डीविमान पर (शहर) ए, बी, सी, डीदेश में) अभिव्यक्ति गैर-सकारात्मक होगी। इसके लिए दो मामलों पर विचार किया जाना चाहिए। 1. मान लें कि अंक ए, बी, सी, डी
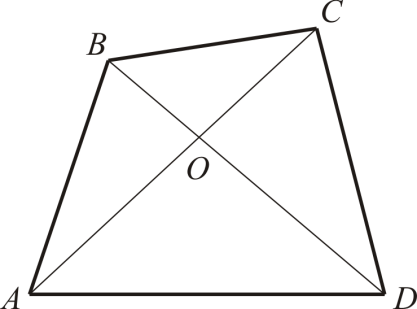
ए बी सी डीविकर्णों के साथ एसीतथा बीडी. फिर हम त्रिभुजों के लिए क्रमिक रूप से त्रिभुज असमिकाएँ लिखते हैं एबीसी, बीसीडी, सीडीएतथा डी ए बी(अंजीर देखें। 2): अब + ईसा पूर्व > एसी; ईसा पूर्व + सीडी > बीडी; सीडी + डीए > सीए; डीए + अब > डी.बी.. सभी चार असमानताओं को जोड़ने पर, हम प्राप्त करते हैं 2. उस मामले पर विचार करें जब बिंदु ए, बी, सी, डी
समतल पर एक चतुर्भुज बनाएँ एसीबीडीविकर्णों के साथ अबतथा सीडी
(अपने लिए एक चित्र बनाएं।) ध्यान दें कि त्रिभुज असमानताएँ पहले मामले की तरह ही त्रिभुजों के लिए होती हैं। यह पता चला है कि समस्या का समाधान वही रहता है, इस तथ्य के बावजूद कि विमान पर बिंदुओं का स्थान काफी बदल गया है। इसे एक और माना जा सकता है विशेषतात्रिभुज असमानता का उपयोग करके समस्याओं के कई समाधान। इसलिए, पहला विमान पहले पहुंचेगा, क्योंकि इसका मार्ग दूसरे से छोटा है। ध्यान दें कि समस्या 5 के समाधान के लिए थोड़ा विश्लेषण की आवश्यकता है, जो सभी ओलंपियाड समस्याओं का एक अनिवार्य गुण है। सावधान रहें - समस्या का आपका समाधान तभी सही होगा जब आप उन सभी संभावित मामलों पर विचार करेंगे जो स्थिति के अनुकूल हों। यह भी ध्यान दिया जाना चाहिए कि अक्सर समस्या की स्थिति को दर्शाने वाली आकृति में, एक त्रिभुज दिखाई नहीं देता है, जिसके लिए त्रिभुज असमानता का अनुप्रयोग एक त्वरित समाधान देगा। इस मामले में, एक अच्छी तरह से चुना गया ज्यामितीय परिवर्तन मदद कर सकता है। हम इस बारे में थोड़ी देर बाद बात करेंगे। इस बिंदु पर त्रिभुज असमानता से परिचित होना पूर्ण घोषित किया जाना चाहिए। लेकिन उनसे नई मुलाकात दूर नहीं है। ग्रेड 7 व्याख्यान 13. त्रिभुज असमानता फिचटे जोहान गॉटलिब (1762-1814) शास्त्रीय जर्मन दर्शन के सबसे प्रमुख प्रतिनिधियों में से एक है। पुस्तक शामिल है उल्लेखनीय कार्य: "चेतना के तथ्य", "मनुष्य का उद्देश्य", "वैज्ञानिक शिक्षण" और अन्य। वर्तमान और पिछली पीढ़ियों के लिए मीडिया और साहित्य में चाहे कितना भी भयावह राष्ट्रीय समाजवाद प्रस्तुत किया जाए, यह लाखों लोगों का ध्यान आकर्षित करना बंद नहीं करता है। सुरक्षा और शक्ति का प्रतीक - पेंटाग्राममार्सियस पेंटाग्राम सबसे महत्वपूर्ण में से एक है जादू के प्रतीक. यह शब्द स्वयं ग्रीक शब्द पेंटे से आया है, जिसका अर्थ है पांच, और ग्रामा, एक अक्षर; पेंटाग्राम - हम ज्यामिति से जानते हैं कि त्रिभुज की दोनों भुजाओं की लंबाई का योग नहीं होता है लंबाई से कमउसकी तीसरी पार्टी। आइए देखें कि हम इस प्रमेय को बीजगणितीय रूप से कैसे व्यक्त कर सकते हैं। एक त्रिभुज पर विचार करें, जैसा कि चित्र में दिखाया गया है। 22. ज्यामितीय असमानता बीजीय त्रिभुज असमानता के बराबर है क्या ज्यामिति का सहारा लिए बिना अंतिम असमानता को सिद्ध करना संभव है? § 8 ch में। III, एक-आयामी मामले के लिए एक प्रमाण दिया गया था (प्रमेय 2, अध्याय III देखें)। जहां असमानता निम्नलिखित रूप लेती है: इस संकेतन में यह समान असमानता की तुलना में अधिक बार होता है त्रिभुज असमानता (4.50) के द्वि-आयामी संस्करण को साबित करने का सबसे आसान तरीका एक समान असमानता साबित करना है। चावल। 22. एक त्रिभुज की असमानता। ऐसा करने के लिए, हम असमानता (4.50) के दोनों हिस्सों को वर्ग करते हैं, और ऐसा करने में हम असमानता पर पहुंचते हैं (4.50) के बराबर। यह देखना आसान है कि अंतिम असमानता निम्नलिखित के बराबर है: लेकिन यह असमानता सुप्रसिद्ध कॉची असमानता का एक सरल परिणाम है [द्वि-आयामी संस्करण, देखें (4.38)] जो त्रिभुज असमानता को सिद्ध करता है। जैसा कि एक-आयामी मामले में, उन स्थितियों को निर्धारित करना मुश्किल नहीं है जिनके तहत त्रिभुज असमानता (4.50) एक समानता बन जाती है। याद रखें कि कॉची की असमानता (4.52) में समानता तभी प्राप्त होती है जब और केवल आनुपातिक हो, यानी जब असमानता (4.51) असमानता के दोनों हिस्सों (4.52) के वर्गमूल को लेकर प्राप्त की जा सकती है। यह कार्रवाई कानूनी है, क्योंकि इसका मतलब बाईं ओर के व्यंजक का गैर-ऋणात्मक वर्गमूल है। मान लीजिए कि (4.52) के दाईं ओर व्यंजक का ऋणात्मक वर्गमूल है। इस मामले में, आनुपातिक होने पर भी, (4.51) में एक सख्त असमानता होगी। इस प्रकार, (4.51) में समानता, और इसलिए त्रिभुज असमानता (4.50) में भी, प्राप्त की जाती है यदि और केवल अगर आनुपातिकता का एक गैर-ऋणात्मक गुणांक है। इस स्थिति का ज्यामितीय अर्थ, जो सूत्र (4.50) में समानता के लिए आवश्यक और पर्याप्त है, इस प्रकार है: अंक (चित्र 21) एक सीधी रेखा से संबंधित होने चाहिए, और बिंदु एक ही तरफ स्थित हैं बिंदु O का। जब त्रिभुज सीधे खंड में बदल जाता है। दूसरे शब्दों में, बिंदु न केवल बिंदु O के साथ एक ही सीधी रेखा पर स्थित हैं, बल्कि मूल O वाली एक ही किरण पर भी स्थित हैं। यह सत्यापित करना आसान है कि यहां प्राप्त स्थितियां एक-आयामी मामले के लिए संगत शर्तों के अनुरूप हैं (असमानताएं जहां समानता हासिल की जाती है यदि और केवल तभी संख्याओं का एक ही चिन्ह होता है। व्युत्पत्ति के समान पथ का अनुसरण करके त्रिभुज असमानता के प्रमाण को सामान्यीकृत किया जा सकता है होल्डर की असमानता, अर्थात् असमानता को साबित करने के लिए किसी भी वास्तविक मूल्यों के लिए धारण करता है, और, पहले की तरह, समानता प्राप्त की जाती है यदि और केवल यदि संख्या आनुपातिक हैं और आनुपातिकता का गुणांक सकारात्मक है। हम अध्याय में इस असमानता पर लौटेंगे। VI, जहां इसके ज्यामितीय अर्थ पर विचार किया जाएगा। आइए त्रिभुज असमानता के एक अन्य प्रमाण की ओर बढ़ते हैं, जिसका उपयोग अधिक सामान्य परिणाम प्राप्त करने के लिए भी किया जा सकता है। एक पहचान है कॉची की असमानता का उपयोग करके एक रूप वर्गमूल[सेमी। (4.51)], दो व्यंजकों पर बारी-बारी से लागू होते हैं।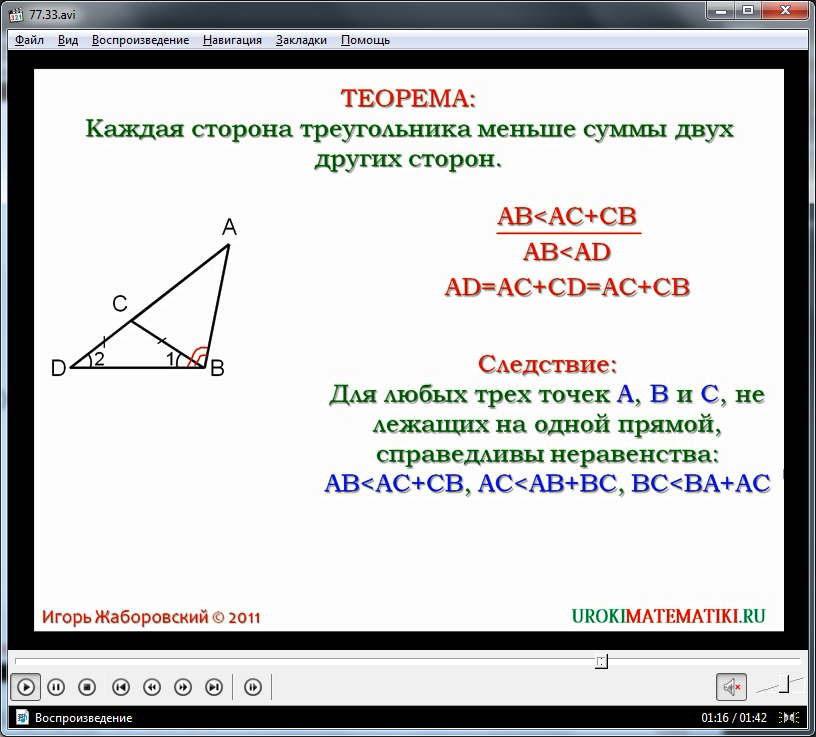
![]()
एक < बी- मतलब कि एककमबी; एक
> बी
- मतलब कि एकअधिकबी; एक
≠ बी- मतलब कि एकबराबर नहींबीया क्या एकतथा बी विभिन्न.
प्रति ढीलाअसमानताओं में निम्नलिखित गणितीय संबंध शामिल हैं: एक ≤ बी- मतलब कि एकइससे कम या इसके बराबरबीया, जो एक ही है, एकअधिक नहीं (अधिक नहीं, अधिक नहीं)बी; एक ≥
बी- मतलब कि एकसे बड़ा या बराबरबीया, जो एक ही है, एककम नहीं हैबी.
फिलहाल, हम असमानताओं को अधिक गहराई से तलाशने की जहमत नहीं उठाएंगे। अभी के लिए, असमानताओं की पहले से ही स्थापित धारणाएँ हमारे लिए पर्याप्त होंगी।
प्रमेय का प्रमाण
. एक त्रिभुज पर विचार करें एबीसीऔर दिखाओ कि अब < एसी + ईसा पूर्व. साबित करते समय, हम एक प्रकार के अतिरिक्त निर्माण का उपयोग करेंगे - समान खंडों को स्थगित करना ( सीधा करने की विधि) एक त्रिभुज में एबीसी(अंजीर। 1) पक्ष की निरंतरता पर ईसा पूर्वखंड स्थगित सीडी, के बराबर एसी. एक समद्विबाहु त्रिभुज में एसीडी
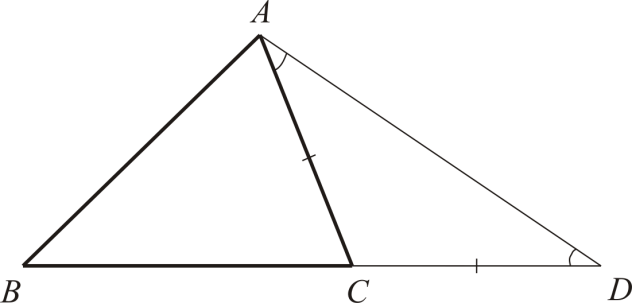
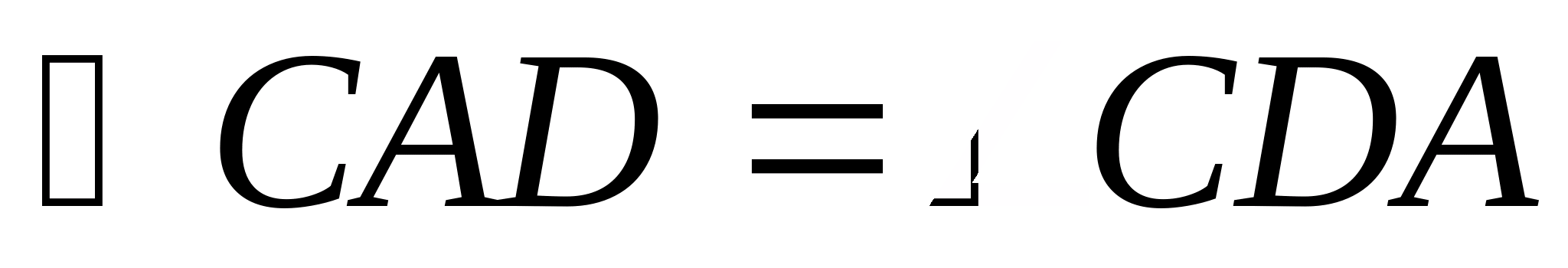 . एक त्रिभुज में अब्दकोना एडी.बी.कोण से कम बुरा, साधन, बीडी > अब, या ईसा पूर्व + सीडी
> अब. परंतु सीडी = एसी, साधन, एसी + ईसा पूर्व > अब. टिप्पणी. कृपया ध्यान दें कि, प्रमेय के निरूपण के आधार पर, तीन असमानताओं को एक साथ लिखा जाना चाहिए: अब < एसी + ईसा पूर्व; एसी< अब + ईसा पूर्व; ईसा पूर्व < अब + एसी. अक्सर, एक असमानता को लिखने के बाद, किसी कारण से वे अन्य दो के बारे में भूल जाते हैं। ध्यान रखें कि इससे कुछ बहुत खराब कीड़े हो सकते हैं। त्रिभुज असमानता सबसे सरल में से एक के रूप में काम कर सकती है एक सीधी रेखा में तीन बिंदुओं से संबंधित मानदंड. त्रिभुज असमानता में समानता प्राप्त होने पर ही तीन बिंदु एक ही सीधी रेखा के होंगे। स्वाभाविक रूप से, समानता केवल तीन असमानताओं में से एक में प्राप्त की जा सकती है (टिप्पणी देखें), क्योंकि एक बिंदु अन्य दो के बीच स्पष्ट रूप से स्थित होगा। एक व्यायाम. सिद्ध कीजिए कि त्रिभुज की प्रत्येक भुजा अन्य दो भुजाओं के अंतर से बड़ी होती है। त्रिभुज असमानता के उपयोग के उदाहरण के रूप में, हम कई अपेक्षाकृत सरल ज्यामितीय समस्याएं देते हैं। कार्य 1. सिद्ध कीजिए कि एक स्वेच्छ चतुर्भुज में ए बी सी डी अब + सीडी < एसी + बीडी.
. एक त्रिभुज में अब्दकोना एडी.बी.कोण से कम बुरा, साधन, बीडी > अब, या ईसा पूर्व + सीडी
> अब. परंतु सीडी = एसी, साधन, एसी + ईसा पूर्व > अब. टिप्पणी. कृपया ध्यान दें कि, प्रमेय के निरूपण के आधार पर, तीन असमानताओं को एक साथ लिखा जाना चाहिए: अब < एसी + ईसा पूर्व; एसी< अब + ईसा पूर्व; ईसा पूर्व < अब + एसी. अक्सर, एक असमानता को लिखने के बाद, किसी कारण से वे अन्य दो के बारे में भूल जाते हैं। ध्यान रखें कि इससे कुछ बहुत खराब कीड़े हो सकते हैं। त्रिभुज असमानता सबसे सरल में से एक के रूप में काम कर सकती है एक सीधी रेखा में तीन बिंदुओं से संबंधित मानदंड. त्रिभुज असमानता में समानता प्राप्त होने पर ही तीन बिंदु एक ही सीधी रेखा के होंगे। स्वाभाविक रूप से, समानता केवल तीन असमानताओं में से एक में प्राप्त की जा सकती है (टिप्पणी देखें), क्योंकि एक बिंदु अन्य दो के बीच स्पष्ट रूप से स्थित होगा। एक व्यायाम. सिद्ध कीजिए कि त्रिभुज की प्रत्येक भुजा अन्य दो भुजाओं के अंतर से बड़ी होती है। त्रिभुज असमानता के उपयोग के उदाहरण के रूप में, हम कई अपेक्षाकृत सरल ज्यामितीय समस्याएं देते हैं। कार्य 1. सिद्ध कीजिए कि एक स्वेच्छ चतुर्भुज में ए बी सी डी अब + सीडी < एसी + बीडी.
समाधान
. होने देना हे- चतुर्भुज के विकर्णों का प्रतिच्छेदन बिंदु ए बी सी डी(रेखा चित्र नम्बर 2)। त्रिभुज असमानता से:
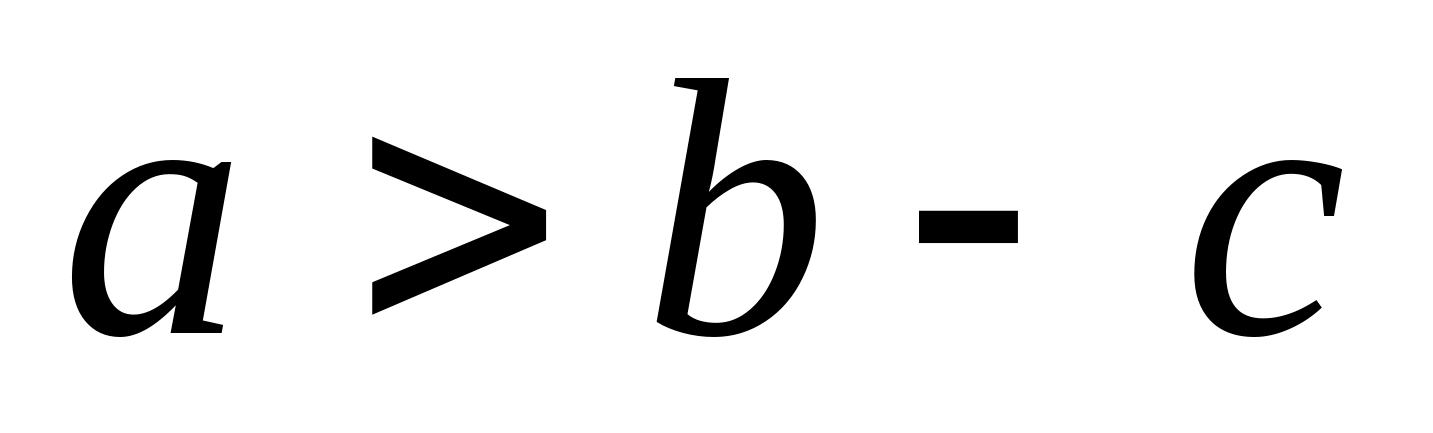 (हम मानते हैं कि
(हम मानते हैं कि 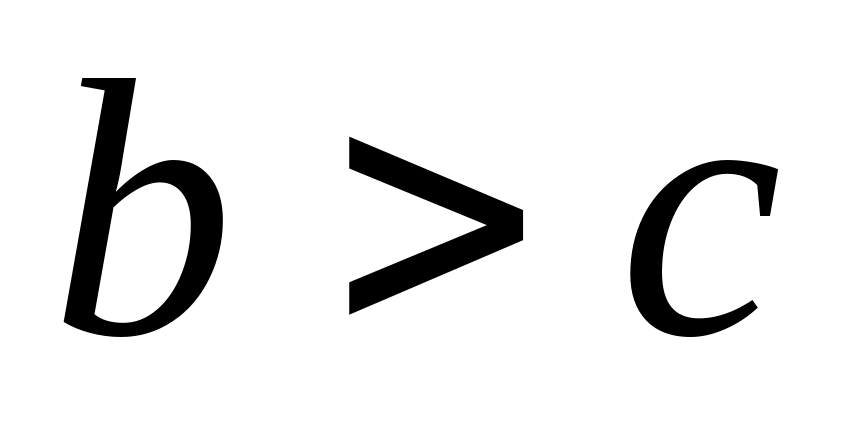 ) फिर, असमानता के दोनों पक्षों को चुकता करने पर, हम प्राप्त करते हैं:
) फिर, असमानता के दोनों पक्षों को चुकता करने पर, हम प्राप्त करते हैं: 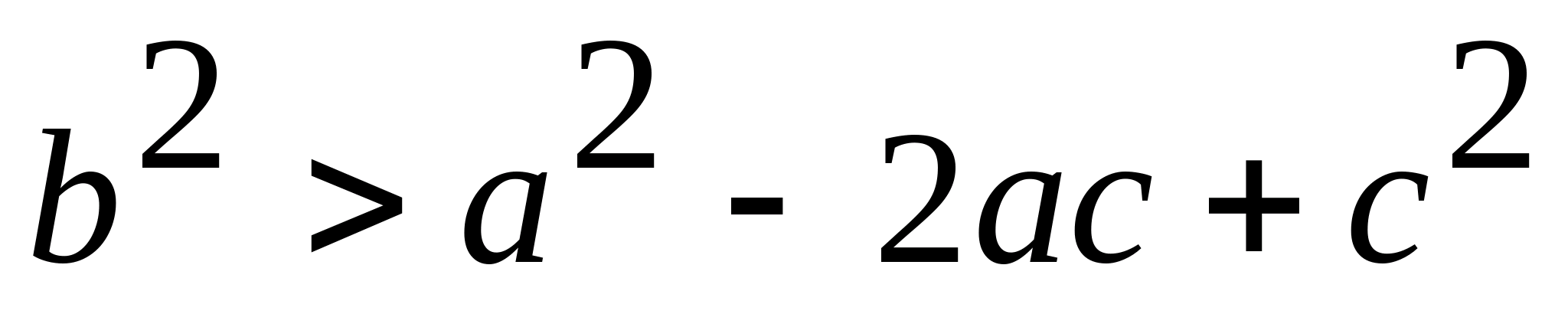 ;
;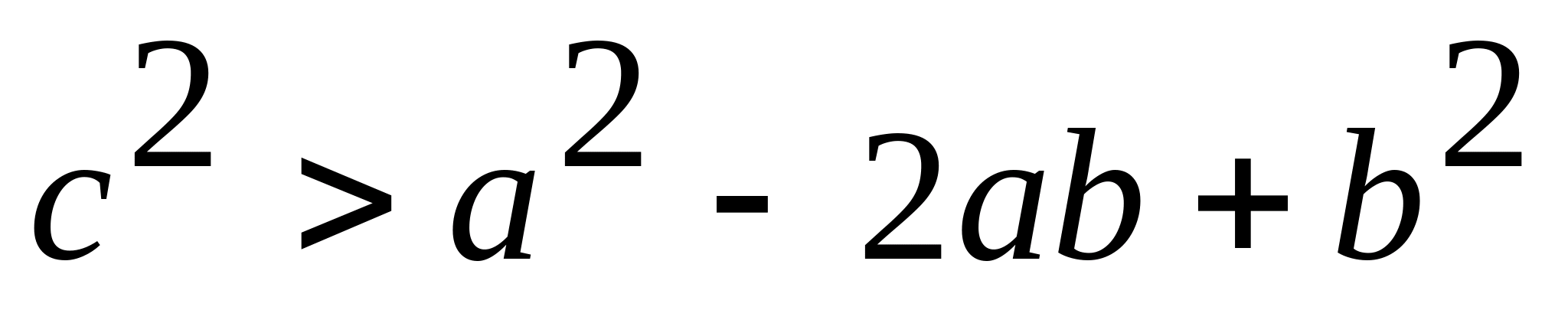 .
.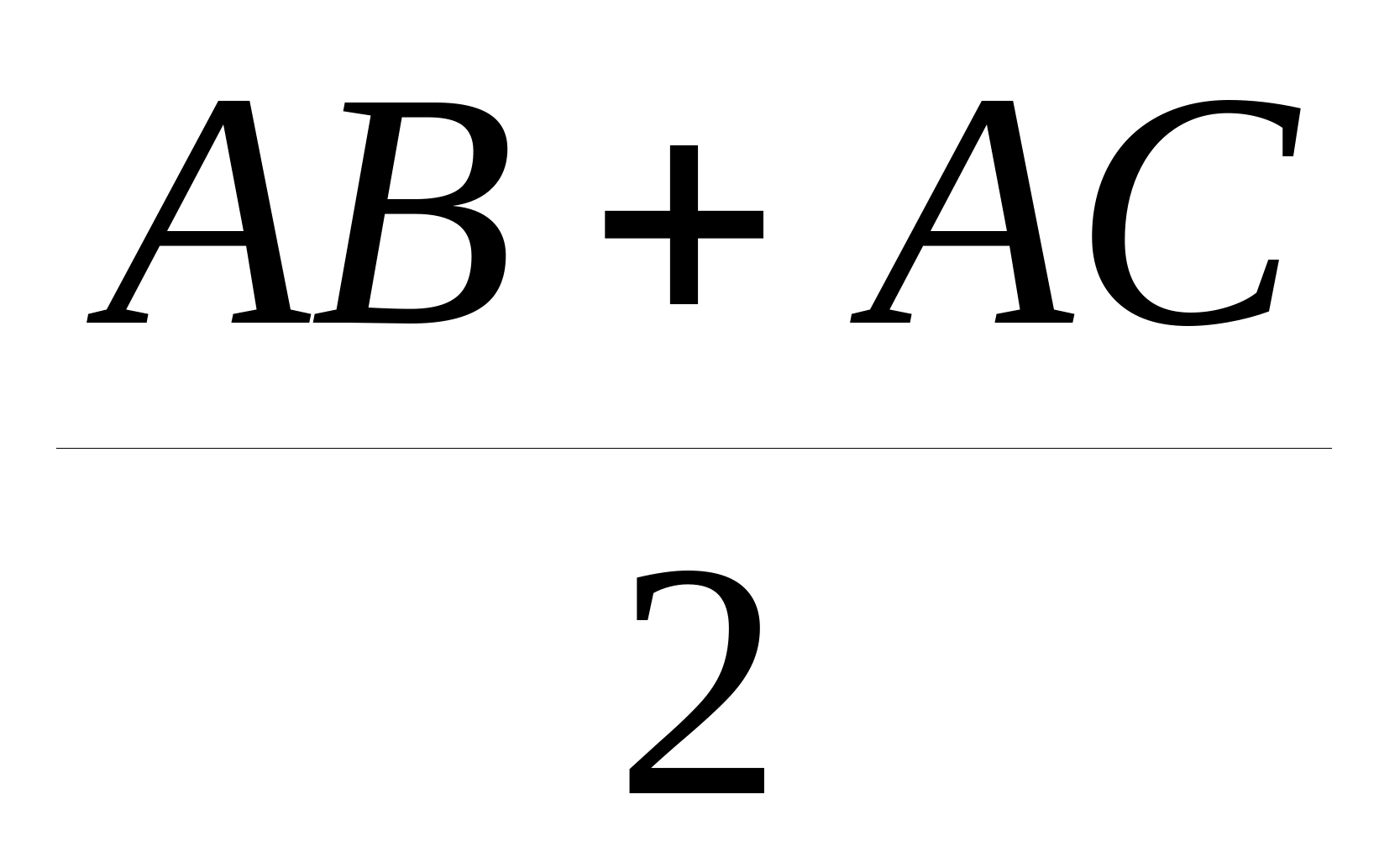 . टास्क 3. समतल पर एक वर्ग दिया गया है ए बी सी डीऔर डॉट हे. सिद्ध कीजिए कि एक बिंदु से दूरी हेवर्ग के किसी एक शीर्ष से दूरियों के योग से अधिक नहीं है हेवर्ग के तीन अन्य शीर्षों तक। समाधान
. त्रिभुज असमानताओं को जोड़ें एसी + ओसी > ओएतथा ओबी + आयुध डिपो > बीडी. इसलिये एसी = बीडी, फिर, कम करने पर, हमें वह मिलता है जिसकी आवश्यकता होती है। टास्क 4. एक उत्तल चतुर्भुज के भीतर एक ऐसा बिंदु ज्ञात कीजिए जिससे उसके शीर्षों तक की दूरी का योग न्यूनतम हो। समाधान
. चूँकि चतुर्भुज उत्तल है, इसके विकर्ण एक बिंदु पर प्रतिच्छेद करते हैं हेइसके अंदर। चतुर्भुज के शीर्षों को निम्न द्वारा निरूपित करें ए, बी, सीतथा डी(दक्षिणावर्त)। तो से दूरियों का योग हेशीर्षों के विकर्णों की लंबाई के योग के बराबर है एसीतथा बीडी. लेकिन किसी अन्य बिंदु के लिए पीहमारे पास, सबसे पहले, कि दूरियों का योग पीऊपर से कम एसी + बीडी, और दूसरी बात, या तो देहात + पीसी > एसी, या पंजाब + पी.डी. > बीडी. तो यह राशि है एसी + बीडीकेवल पीबिंदु के साथ मेल खाता है हे. तो बिंदु हे- इच्छित। त्रिभुज असमानता को भी भ्रमित करने वाली शब्द समस्याओं में सफलतापूर्वक लागू किया जाता है। दिलचस्प बात यह है कि ऐसी समस्याओं में बहुत कुछ इस बात पर निर्भर करता है कि आप कितनी अच्छी तरह से ज्यामितीय व्याख्या करते हैं। टास्क 5. एक निश्चित देश में 4 शहर हैं: ए, बी, सीतथा डी. एक ही समय में दो विमानों ने शहर से उड़ान भरी ए. पहले विमान का मार्ग: ए-बी-डी-सी-ए-डी-बी-सी-ए, और दूसरे का मार्ग: ए-बी-सी-डी-ए-बी-सी-डी-ए-बी-सी-डी-ए. यदि उनकी गति समान हो तो कौन सा विमान पहले अपना मार्ग पूरा करेगा? प्रयोग करने से डरो मत! यदि समस्या में वस्तुओं का एक विशिष्ट स्थान निर्दिष्ट नहीं है, तो आपको अपने समाधान में वह सब कुछ आकर्षित करने का अधिकार है जो शर्त का खंडन नहीं करता है - यह आपका है, आखिरकार। टास्क 5 में शहरों को शामिल करते हुए, आप अपनी इच्छानुसार व्यवस्था कर सकते हैं। केवल यह याद रखना चाहिए कि कुछ समस्याओं में, "सामान्य" को पार्स करने के बाद, सामान्य मामला, कुछ "पैथोलॉजिकल", विशेष मामलों का विश्लेषण करना आवश्यक है। उदाहरण के लिए, समस्या 5 में आपको उस मामले पर विचार करने की आवश्यकता हो सकती है जहां कुछ तीन शहर एक ही रेखा पर स्थित हैं - यह सब इस बात पर निर्भर करता है कि सामान्य मामले के लिए आपका समाधान क्या है। समस्या 5 समाधान
. हम प्रत्येक विमान के मार्गों की लंबाई को शहरों के बीच की दूरी के योग के रूप में लिखते हैं। पहले विमान के मार्ग की लंबाई बराबर होगी
. टास्क 3. समतल पर एक वर्ग दिया गया है ए बी सी डीऔर डॉट हे. सिद्ध कीजिए कि एक बिंदु से दूरी हेवर्ग के किसी एक शीर्ष से दूरियों के योग से अधिक नहीं है हेवर्ग के तीन अन्य शीर्षों तक। समाधान
. त्रिभुज असमानताओं को जोड़ें एसी + ओसी > ओएतथा ओबी + आयुध डिपो > बीडी. इसलिये एसी = बीडी, फिर, कम करने पर, हमें वह मिलता है जिसकी आवश्यकता होती है। टास्क 4. एक उत्तल चतुर्भुज के भीतर एक ऐसा बिंदु ज्ञात कीजिए जिससे उसके शीर्षों तक की दूरी का योग न्यूनतम हो। समाधान
. चूँकि चतुर्भुज उत्तल है, इसके विकर्ण एक बिंदु पर प्रतिच्छेद करते हैं हेइसके अंदर। चतुर्भुज के शीर्षों को निम्न द्वारा निरूपित करें ए, बी, सीतथा डी(दक्षिणावर्त)। तो से दूरियों का योग हेशीर्षों के विकर्णों की लंबाई के योग के बराबर है एसीतथा बीडी. लेकिन किसी अन्य बिंदु के लिए पीहमारे पास, सबसे पहले, कि दूरियों का योग पीऊपर से कम एसी + बीडी, और दूसरी बात, या तो देहात + पीसी > एसी, या पंजाब + पी.डी. > बीडी. तो यह राशि है एसी + बीडीकेवल पीबिंदु के साथ मेल खाता है हे. तो बिंदु हे- इच्छित। त्रिभुज असमानता को भी भ्रमित करने वाली शब्द समस्याओं में सफलतापूर्वक लागू किया जाता है। दिलचस्प बात यह है कि ऐसी समस्याओं में बहुत कुछ इस बात पर निर्भर करता है कि आप कितनी अच्छी तरह से ज्यामितीय व्याख्या करते हैं। टास्क 5. एक निश्चित देश में 4 शहर हैं: ए, बी, सीतथा डी. एक ही समय में दो विमानों ने शहर से उड़ान भरी ए. पहले विमान का मार्ग: ए-बी-डी-सी-ए-डी-बी-सी-ए, और दूसरे का मार्ग: ए-बी-सी-डी-ए-बी-सी-डी-ए-बी-सी-डी-ए. यदि उनकी गति समान हो तो कौन सा विमान पहले अपना मार्ग पूरा करेगा? प्रयोग करने से डरो मत! यदि समस्या में वस्तुओं का एक विशिष्ट स्थान निर्दिष्ट नहीं है, तो आपको अपने समाधान में वह सब कुछ आकर्षित करने का अधिकार है जो शर्त का खंडन नहीं करता है - यह आपका है, आखिरकार। टास्क 5 में शहरों को शामिल करते हुए, आप अपनी इच्छानुसार व्यवस्था कर सकते हैं। केवल यह याद रखना चाहिए कि कुछ समस्याओं में, "सामान्य" को पार्स करने के बाद, सामान्य मामला, कुछ "पैथोलॉजिकल", विशेष मामलों का विश्लेषण करना आवश्यक है। उदाहरण के लिए, समस्या 5 में आपको उस मामले पर विचार करने की आवश्यकता हो सकती है जहां कुछ तीन शहर एक ही रेखा पर स्थित हैं - यह सब इस बात पर निर्भर करता है कि सामान्य मामले के लिए आपका समाधान क्या है। समस्या 5 समाधान
. हम प्रत्येक विमान के मार्गों की लंबाई को शहरों के बीच की दूरी के योग के रूप में लिखते हैं। पहले विमान के मार्ग की लंबाई बराबर होगीफिचटे जोहान गॉटलिब (1762-1814) शास्त्रीय जर्मन दर्शन के सबसे प्रमुख प्रतिनिधियों में से एक। पुस्तक में प्रसिद्ध कार्य शामिल हैं: "चेतना के तथ्य", "मनुष्य का उद्देश्य", "विज्ञान" और अन्य पुस्तकें
किताबजोसेफ आर्थर गोबिन्यू। मानव जाति की असमानता पर अनुभव पुस्तक
किताबपेंटाग्राम सबसे महत्वपूर्ण जादुई प्रतीकों में से एक है। यह शब्द स्वयं ग्रीक शब्द "पेंटे" से आया है जिसका अर्थ है पांच, और "ग्रामा" अक्षर
दस्तावेज़