पहली उल्लेखनीय सीमा का अनुप्रयोग। पहली उल्लेखनीय सीमा: सिद्धांत और उदाहरण

अद्भुत सीमाएं खोजेंयह न केवल अध्ययन के पहले, दूसरे वर्ष के कई छात्रों के लिए मुश्किल है, जो सीमा के सिद्धांत का अध्ययन करते हैं, बल्कि कुछ शिक्षकों के लिए भी मुश्किल है।

पहली उल्लेखनीय सीमा का सूत्र

पहली उल्लेखनीय सीमा के परिणाम सूत्र लिखें
1. 2. 3. 4. लेकिन अपने आप में, उल्लेखनीय सीमा के सामान्य सूत्र किसी परीक्षा या परीक्षा में किसी की मदद नहीं करते हैं। लब्बोलुआब यह है कि वास्तविक कार्यों का निर्माण किया जाता है ताकि ऊपर लिखे गए सूत्रों पर अभी भी पहुंचने की आवश्यकता हो। और अधिकांश छात्र जो कक्षाएं छोड़ते हैं, पत्राचार द्वारा इस पाठ्यक्रम का अध्ययन करते हैं या ऐसे शिक्षक होते हैं जो स्वयं हमेशा यह नहीं समझते हैं कि वे किस बारे में समझा रहे हैं, वे सबसे प्राथमिक उदाहरणों की गणना उल्लेखनीय सीमा तक नहीं कर सकते हैं। पहली उल्लेखनीय सीमा के सूत्रों से, हम देखते हैं कि उनका उपयोग त्रिकोणमितीय कार्यों वाले व्यंजकों के लिए शून्य से विभाजित शून्य जैसी अनिश्चितताओं की जांच के लिए किया जा सकता है। पहले पर कई उदाहरणों पर विचार करें अद्भुत सीमा y, और फिर हम दूसरी उल्लेखनीय सीमा का अध्ययन करेंगे।

उदाहरण 1. फलन की सीमा ज्ञात कीजिए sin(7*x)/(5*x)
समाधान: जैसा कि आप देख सकते हैं, सीमा के तहत फ़ंक्शन पहली उल्लेखनीय सीमा के करीब है, लेकिन फ़ंक्शन की सीमा निश्चित रूप से एक के बराबर नहीं है। सीमा के लिए इस तरह के असाइनमेंट में, किसी को हर में एक समान गुणांक के साथ एक चर को एकल करना चाहिए जो कि साइन के तहत चर में निहित है। इस मामले में, 7 . से विभाजित और गुणा करें

कुछ के लिए, इस तरह का विवरण अनावश्यक प्रतीत होगा, लेकिन अधिकांश छात्रों के लिए जो सीमाएं देना मुश्किल लगता है, यह नियमों को बेहतर ढंग से समझने और सैद्धांतिक सामग्री सीखने में मदद करेगा।
इसके अलावा, अगर वहाँ है उल्टा दृश्यकार्य भी पहली उल्लेखनीय सीमा है। और सभी क्योंकि अद्भुत सीमा एक के बराबर है

1 उल्लेखनीय सीमा के परिणामों पर भी यही नियम लागू होता है। इसलिए, यदि आपसे पूछा जाए कि "पहली अद्भुत सीमा क्या है?" आपको बिना किसी हिचकिचाहट के उत्तर देना चाहिए कि यह एक इकाई है।

उदाहरण 2. फलन sin(6x)/tan(11x) की सीमा ज्ञात कीजिए।
हल: अंतिम परिणाम को समझने के लिए, हम फंक्शन को फॉर्म में लिखते हैं

उल्लेखनीय सीमा के नियमों को लागू करने के लिए गुणनखंडों से गुणा और भाग करें

इसके बाद, हम सीमाओं के उत्पाद के संदर्भ में कार्यों के उत्पाद की सीमा लिखते हैं

जटिल सूत्रों के बिना, हमें कुछ त्रिकोणमितीय फलनों की सीमा ज्ञात हुई। आत्मसात करने के लिए सरल सूत्रअद्भुत सीमा के कोरोलरी 1 के सूत्र, 2 और 4 की सीमा ज्ञात करने का प्रयास करें। हम अधिक जटिल कार्यों पर विचार करेंगे।

उदाहरण 3. सीमा की गणना करें (1-cos(x))/x^2
हल: प्रतिस्थापन द्वारा जाँच करने पर, हमें अनिश्चितता 0/0 प्राप्त होती है। बहुत से लोग नहीं जानते कि इस तरह के उदाहरण को 1 अद्भुत सीमा तक कैसे कम किया जाए। यहां आपको त्रिकोणमितीय सूत्र का उपयोग करना चाहिए

इस मामले में, सीमा एक स्पष्ट रूप में बदल जाएगी

हम फलन को एक उल्लेखनीय सीमा के वर्ग तक कम करने में सफल रहे हैं।

उदाहरण 4. सीमा ज्ञात कीजिए
समाधान: प्रतिस्थापित करते समय, हमें परिचित विशेषता 0/0 प्राप्त होती है। हालांकि, वेरिएबल पाई के करीब पहुंचता है, शून्य के करीब नहीं। इसलिए, पहली उल्लेखनीय सीमा को लागू करने के लिए, हम चर x में ऐसा परिवर्तन करेंगे, जिससे नया चर शून्य हो जाए। ऐसा करने के लिए, हम हर को नए चर Pi-x=y . के रूप में निरूपित करते हैं

इस प्रकार, पिछले कार्य में दिए गए त्रिकोणमितीय सूत्र का उपयोग करके, उदाहरण को 1 अद्भुत सीमा तक घटा दिया जाता है।

उदाहरण 5 सीमा की गणना करें
समाधान: पहले तो यह स्पष्ट नहीं है कि सीमाओं को कैसे सरल बनाया जाए। लेकिन अगर कोई उदाहरण है, तो उसका जवाब होना चाहिए। तथ्य यह है कि चर एकता में जाता है, प्रतिस्थापित करते समय, फॉर्म शून्य की एक विलक्षणता को अनंत से गुणा किया जाता है, इसलिए स्पर्शरेखा को सूत्र द्वारा प्रतिस्थापित किया जाना चाहिए

उसके बाद, हमें वांछित अनिश्चितता 0/0 मिलती है। इसके बाद, हम सीमा में चरों का परिवर्तन करते हैं, और कोटैंजेंट की आवधिकता का उपयोग करते हैं

अंतिम प्रतिस्थापन हमें उल्लेखनीय सीमा के कोरोलरी 1 का उपयोग करने की अनुमति देते हैं।

दूसरी उल्लेखनीय सीमा घातांक के बराबर है

यह एक क्लासिक है जिसमें वास्तविक समस्याओं की सीमा तक पहुंचना हमेशा आसान नहीं होता है।
गणना के लिए आपको आवश्यकता होगी सीमाएं दूसरी उल्लेखनीय सीमा के परिणाम हैं:
1. 2. 3. 4.
दूसरी उल्लेखनीय सीमा और उसके परिणामों के लिए धन्यवाद, कोई भी अनिश्चितताओं का पता लगा सकता है जैसे शून्य को शून्य से विभाजित करना, एक को अनंत की शक्ति के लिए, और अनंत को अनंत से विभाजित करना, और यहां तक कि एक ही डिग्री तक।

आइए कुछ सरल उदाहरणों से शुरू करते हैं।

उदाहरण 6 किसी फ़ंक्शन की सीमा ज्ञात करें
समाधान: सीधे 2 अद्भुत सीमा लागू करने से काम नहीं चलेगा। सबसे पहले आपको संकेतक को चालू करने की आवश्यकता है ताकि इसका रूप कोष्ठक में शब्द के विपरीत हो

यह 2 उल्लेखनीय सीमा को कम करने की तकनीक है और वास्तव में, सीमा के परिणाम के 2 सूत्र की व्युत्पत्ति।

उदाहरण 7 किसी फ़ंक्शन की सीमा ज्ञात करें
समाधान: हमारे पास उल्लेखनीय सीमा के कोरोलरी 2 के 3 सूत्र के लिए कार्य हैं। शून्य प्रतिस्थापन 0/0 के रूप की विलक्षणता देता है। नियम के तहत सीमा बढ़ाने के लिए, हम हर को घुमाते हैं ताकि चर का वही गुणांक हो जो लघुगणक में है

परीक्षा को समझना और प्रदर्शन करना भी आसान है। सीमाओं की गणना में छात्रों की कठिनाइयाँ निम्नलिखित कार्यों से शुरू होती हैं।

उदाहरण 8 फ़ंक्शन सीमा की गणना करें[(x+7)/(x-3)]^(x-2)
हल: हमारे पास अनंत की घात के लिए टाइप 1 की विलक्षणता है। यदि आप मुझ पर विश्वास नहीं करते हैं, तो आप हर जगह "x" के बजाय अनंत को प्रतिस्थापित कर सकते हैं और अपने लिए देख सकते हैं। नियम के तहत उठाने के लिए, हम अंश को हर द्वारा कोष्ठक में विभाजित करते हैं, इसके लिए हम पहले जोड़तोड़ करते हैं

व्यंजक को सीमा में बदलें और इसे 2 अद्भुत सीमा में बदलें

सीमा 10 की शक्ति का घातांक है। स्थिरांक जो कि कोष्ठक और डिग्री दोनों में एक चर के साथ शब्द हैं, किसी भी "मौसम" का योगदान नहीं करते हैं - इसे याद रखना चाहिए। और अगर शिक्षक आपसे पूछें - "आप संकेतक क्यों नहीं घुमाते?" (इस उदाहरण के लिए x-3 में), फिर कहें कि "जब चर अनंत तक जाता है, तो इसमें 100 जोड़ें, या 1000 घटाएं, और सीमा वही रहेगी!"।
इस प्रकार की सीमाओं की गणना करने का दूसरा तरीका है। हम इसके बारे में अगले कार्य में बात करेंगे।

उदाहरण 9 सीमा का पता लगाएं
हल: अब हम अंश और हर में चर निकालते हैं और एक विशेषता को दूसरे में बदलते हैं। अंतिम मान प्राप्त करने के लिए, हम उल्लेखनीय सीमा के कोरोलरी 2 के सूत्र का उपयोग करते हैं

उदाहरण 10 किसी फ़ंक्शन की सीमा ज्ञात करें
हल: हर कोई दी गई सीमा का पता नहीं लगा सकता है। सीमा को 2 तक बढ़ाने के लिए, कल्पना करें कि पाप (3x) एक चर है, और आपको घातांक को मोड़ना होगा

इसके बाद, हम संकेतक को डिग्री में डिग्री के रूप में लिखते हैं

कोष्ठक में मध्यवर्ती तर्कों का वर्णन किया गया है। पहली और दूसरी अद्भुत सीमाओं का उपयोग करने के परिणामस्वरूप, हमें घन घातांक मिला।

उदाहरण 11. फ़ंक्शन सीमा की गणना करेंपाप(2*x)/लॉग(3*x+1)
हल: हमें फॉर्म 0/0 की अनिश्चितता है। इसके अलावा, हम देखते हैं कि फ़ंक्शन को दोनों अद्भुत सीमाओं के उपयोग में परिवर्तित किया जाना चाहिए। आइए पिछले गणितीय परिवर्तन करते हैं

इसके अलावा, बिना किसी कठिनाई के, सीमा मान लेती है

इस तरह आप परीक्षण, परीक्षण, मॉड्यूल पर सहज महसूस करेंगे यदि आप सीखते हैं कि कैसे कार्यों को जल्दी से पेंट करना है और उन्हें पहली या दूसरी अद्भुत सीमा तक कम करना है। यदि आपके लिए सीमा खोजने के उपरोक्त तरीकों को याद रखना मुश्किल है, तो आप हमेशा ऑर्डर कर सकते हैं परीक्षणहमारी सीमा तक।
ऐसा करने के लिए, फॉर्म भरें, डेटा निर्दिष्ट करें और उदाहरणों के साथ एक फ़ाइल संलग्न करें। हमने कई छात्रों की मदद की है - हम आपकी भी मदद कर सकते हैं!

पहली उल्लेखनीय सीमा का उपयोग अक्सर साइन, आर्क्सिन, स्पर्शरेखा, आर्कटिक और परिणामी अनिश्चितताओं को शून्य से विभाजित करने वाली सीमाओं की गणना के लिए किया जाता है।

सूत्र

पहली उल्लेखनीय सीमा का सूत्र है: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$

हम देखते हैं कि $ \alpha\to 0 $ से $ \sin\alpha \to 0 $ प्राप्त होता है, इस प्रकार हमारे पास अंश और हर में शून्य होता है। इस प्रकार, $ \frac(0)(0) $ की अनिश्चितताओं को प्रकट करने के लिए पहली उल्लेखनीय सीमा के सूत्र की आवश्यकता है।

फॉर्मूले को लागू करने के लिए, दो शर्तों को पूरा करना होगा:

एक भिन्न की ज्या और हर में निहित व्यंजक समान होते हैं
एक भिन्न की ज्या और हर में व्यंजक शून्य हो जाते हैं

ध्यान! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ हालांकि साइन के नीचे और हर में भाव समान हैं, हालांकि $ 2x ^2+1 = 1 $, जब $ x\to 0 $। दूसरी शर्त पूरी नहीं हुई है, इसलिए सूत्र लागू नहीं किया जा सकता है!

परिणाम

बहुत कम ही, कार्यों में आप एक साफ पहली अद्भुत सीमा देख सकते हैं जिसमें आप तुरंत उत्तर लिख सकते हैं। व्यवहार में, सब कुछ थोड़ा अधिक जटिल लगता है, लेकिन ऐसे मामलों के लिए पहली उल्लेखनीय सीमा के परिणामों को जानना उपयोगी होगा। उनके लिए धन्यवाद, आप जल्दी से वांछित सीमा की गणना कर सकते हैं।

$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$

$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$

समाधान उदाहरण

आइए पहली उल्लेखनीय सीमा पर विचार करें, जिसके उदाहरण त्रिकोणमितीय कार्यों और अनिश्चितता $ \bigg[\frac(0)(0)\bigg] $ वाली सीमाओं की गणना के लिए समाधान हैं।

उदाहरण 1
गणना $ \lim_(x\to 0) \frac(\sin2x)(4x) $
समाधान
सीमा पर विचार करें और ध्यान दें कि इसमें एक ज्या है। इसके बाद, हम अंश और हर में $ x = 0 $ को प्रतिस्थापित करते हैं और शून्य की अनिश्चितता को शून्य से विभाजित करते हैं: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)( 0) $$ पहले से ही दो संकेत हैं कि आपको एक अद्भुत सीमा लागू करने की आवश्यकता है, लेकिन एक छोटी सी बारीकियां है: हम सूत्र को तुरंत लागू नहीं कर पाएंगे, क्योंकि साइन साइन के तहत अभिव्यक्ति हर में अभिव्यक्ति से भिन्न होती है। और हमें उनके बराबर होने की जरूरत है। इसलिए, मदद से प्राथमिक परिवर्तनअंश हम इसे $2x$ में बदल देते हैं। ऐसा करने के लिए, हम एक अलग कारक द्वारा भिन्न के हर से ड्यूस निकालेंगे। यह इस तरह दिखता है: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ , कि अंत में $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ सूत्र द्वारा प्राप्त किया गया था। यदि आप अपनी समस्या का समाधान नहीं कर सकते हैं, तो हमें भेजें। हम देंगे विस्तृत समाधान. आप गणना की प्रगति से खुद को परिचित करने और जानकारी इकट्ठा करने में सक्षम होंगे। इससे आपको समय पर शिक्षक से क्रेडिट प्राप्त करने में मदद मिलेगी!
उत्तर
$$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$

उदाहरण 2
$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ खोजें
समाधान
हमेशा की तरह, आपको सबसे पहले अनिश्चितता के प्रकार को जानना होगा। यदि इसे शून्य से शून्य से विभाजित किया जाता है, तो हम एक ज्या की उपस्थिति पर ध्यान देते हैं: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ यह अनिश्चितता हमें पहली उल्लेखनीय सीमा के सूत्र का उपयोग करने की अनुमति देती है, लेकिन हर से अभिव्यक्ति साइन के तर्क के बराबर नहीं है? इसलिए, "माथे पर" सूत्र लागू करना असंभव है। आपको साइन तर्क से अंश को गुणा और विभाजित करने की आवश्यकता है: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x-x^ 4)(x ^3+2x)) = $$ अब हम सीमाओं के गुणों का वर्णन करते हैं: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x-x^4 )\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ दूसरी सीमा केवल सूत्र में फिट होती है और एक के बराबर होती है: $ $ = \lim_(x\to 0) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x)(2x- x^4) = $$ फिर से $ x = 0 $ को भिन्न में रखें और अनिश्चितता $ \frac(0)(0) $ प्राप्त करें। इसे खत्म करने के लिए, कोष्ठक में से $ x $ निकालना और इसे कम करना पर्याप्त है: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^) 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2)(2) = 1 $$
उत्तर
$$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$

उदाहरण 4
गणना $ \lim_(x\to0) \frac(\sin2x)(tg3x) $
समाधान
आइए $ x = 0 $ को प्रतिस्थापित करके गणना शुरू करें। परिणामस्वरूप, हमें अनिश्चितता $ \frac(0)(0) $ मिलती है। सीमा में एक साइन और एक स्पर्शरेखा होती है, जो पहली उल्लेखनीय सीमा के सूत्र का उपयोग करके स्थिति के संभावित विकास पर संकेत देती है। आइए भिन्न के अंश और हर को एक सूत्र और परिणाम में बदलें: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ अब हम देखते हैं कि अंश और हर में सूत्र और परिणामों के लिए उपयुक्त व्यंजक हैं। संबंधित हर के लिए ज्या तर्क और स्पर्शरेखा तर्क समान हैं $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$
उत्तर
$$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$

लेख में: "पहली उल्लेखनीय सीमा, समाधान के उदाहरण" उन मामलों के बारे में बताया गया था जिनमें इस सूत्र और इसके परिणामों का उपयोग करने की सलाह दी जाती है।

ऊपर दिए गए लेख से आप पता लगा सकते हैं कि सीमा क्या है और इसके साथ क्या खाया जाता है - यह बहुत महत्वपूर्ण है। क्यों? आप यह नहीं समझ सकते हैं कि निर्धारक क्या हैं और उन्हें सफलतापूर्वक हल करें, हो सकता है कि आप यह बिल्कुल न समझें कि व्युत्पन्न क्या है और उन्हें "पांच" पर खोजें। लेकिन अगर आपको समझ में नहीं आता कि सीमा क्या है, तो व्यावहारिक कार्यों को हल करना मुश्किल होगा। इसके अलावा, निर्णयों के डिजाइन के नमूनों और डिजाइन के लिए मेरी सिफारिशों के साथ खुद को परिचित करना अतिश्योक्तिपूर्ण नहीं होगा। सभी जानकारी सरल और सुलभ तरीके से प्रस्तुत की जाती है।

और इस पाठ के प्रयोजनों के लिए, हमें निम्नलिखित कार्यप्रणाली सामग्री की आवश्यकता है: उल्लेखनीय सीमाएंतथा त्रिकोणमितीय सूत्र. वे पृष्ठ पर पाए जा सकते हैं। मैनुअल प्रिंट करना सबसे अच्छा है - यह बहुत अधिक सुविधाजनक है, इसके अलावा, उन्हें अक्सर ऑफ़लाइन एक्सेस करना पड़ता है।

अद्भुत सीमाओं के बारे में क्या उल्लेखनीय है? इन सीमाओं की उल्लेखनीयता इस तथ्य में निहित है कि वे प्रसिद्ध गणितज्ञों के महानतम दिमागों द्वारा सिद्ध किए गए थे, और आभारी वंशजों को त्रिकोणमितीय कार्यों, लघुगणक और डिग्री के ढेर के साथ भयानक सीमाओं से पीड़ित नहीं होना पड़ता है। यही है, सीमा खोजने पर, हम तैयार किए गए परिणामों का उपयोग करेंगे जो सैद्धांतिक रूप से सिद्ध हो चुके हैं।

कई उल्लेखनीय सीमाएँ हैं, लेकिन व्यवहार में, 95% मामलों में अंशकालिक छात्रों की दो उल्लेखनीय सीमाएँ हैं: पहली अद्भुत सीमा, दूसरी अद्भुत सीमा. यह ध्यान दिया जाना चाहिए कि ये ऐतिहासिक रूप से स्थापित नाम हैं, और जब, उदाहरण के लिए, वे "पहली अद्भुत सीमा" के बारे में बात करते हैं, तो उनका मतलब यह एक बहुत ही विशिष्ट चीज है, न कि छत से ली गई कुछ यादृच्छिक सीमा।

पहली अद्भुत सीमा

निम्नलिखित सीमा पर विचार करें: (मूल अक्षर "वह" के बजाय मैं उपयोग करूंगा ग्रीक अक्षर"अल्फा", सामग्री की प्रस्तुति के संदर्भ में यह अधिक सुविधाजनक है)।

सीमा ज्ञात करने के हमारे नियम के अनुसार (लेख देखें .) सीमाएं। समाधान उदाहरण) हम फ़ंक्शन में शून्य को स्थानापन्न करने का प्रयास करते हैं: अंश में हमें शून्य मिलता है (शून्य की साइन शून्य है), हर में, जाहिर है, शून्य भी। इस प्रकार, हम प्रपत्र की अनिश्चितता का सामना कर रहे हैं, जिसे सौभाग्य से, प्रकट करने की आवश्यकता नहीं है। मैं जानता हूँ गणितीय विश्लेषण, यह साबित होता है कि:

इस गणितीय तथ्य को कहा जाता है पहली अद्भुत सीमा. मैं सीमा का विश्लेषणात्मक प्रमाण नहीं दूंगा, लेकिन यहाँ यह है ज्यामितीय अर्थआइए सबक पर एक नज़र डालें अतिसूक्ष्म कार्य.

अक्सर व्यावहारिक कार्यों में, कार्यों को अलग तरह से व्यवस्थित किया जा सकता है, इससे कुछ भी नहीं बदलता है:

- वही पहली अद्भुत सीमा।

लेकिन आप अंश और हर को स्वयं पुनर्व्यवस्थित नहीं कर सकते! यदि प्रपत्र में एक सीमा दी गई है, तो उसे उसी रूप में हल किया जाना चाहिए, बिना कुछ पुनर्व्यवस्थित किए।

व्यवहार में, न केवल एक चर एक पैरामीटर के रूप में कार्य कर सकता है, बल्कि एक प्राथमिक कार्य भी कर सकता है, जटिल कार्य. यह केवल इतना महत्वपूर्ण है कि यह शून्य हो जाता है.

उदाहरण:
, , ,

यहां , , , , और सब कुछ गुलजार है - पहली अद्भुत सीमा लागू होती है।

और यहाँ अगली प्रविष्टि है - विधर्म:

क्यों? क्योंकि बहुपद शून्य की ओर प्रवृत्त नहीं होता है, यह पाँच की ओर प्रवृत्त होता है।

वैसे सवाल बैकफिलिंग का है, लेकिन लिमिट क्या है? ? उत्तर पाठ के अंत में पाया जा सकता है।

व्यवहार में, सब कुछ इतना आसान नहीं है, लगभग कभी भी एक छात्र को एक मुफ्त सीमा को हल करने और एक आसान क्रेडिट प्राप्त करने की पेशकश नहीं की जाएगी। हम्म्... मैं ये पंक्तियाँ लिख रहा हूँ, और एक बहुत ही महत्वपूर्ण विचार मन में आया - आखिरकार, "मुक्त" गणितीय परिभाषाओं और सूत्रों को दिल से याद रखना बेहतर लगता है, यह परीक्षण में अमूल्य मदद हो सकती है, जब मुद्दा "दो" और "तीन" के बीच तय किया जाएगा, और शिक्षक छात्र से कुछ सरल प्रश्न पूछने या हल करने की पेशकश करने का फैसला करता है सबसे सरल उदाहरण("शायद वह (ए) अभी भी जानता है क्या?")।

आइए विचार पर चलते हैं व्यावहारिक उदाहरण:

उदाहरण 1

सीमा का पता लगाएं

यदि हम सीमा में कोई साइन देखते हैं, तो इससे हमें तुरंत पहली उल्लेखनीय सीमा को लागू करने की संभावना के बारे में सोचना चाहिए।

सबसे पहले, हम सीमा चिह्न के तहत अभिव्यक्ति में 0 को प्रतिस्थापित करने का प्रयास करते हैं (हम इसे मानसिक रूप से या मसौदे पर करते हैं):

तो, हमारे पास रूप की एक अनिश्चितता है, इसकी इंगित करना सुनिश्चित करेंनिर्णय लेने में। सीमा चिह्न के तहत अभिव्यक्ति पहली अद्भुत सीमा की तरह दिखती है, लेकिन यह काफी नहीं है, यह साइन के तहत है, लेकिन हर में है।

ऐसे मामलों में, हमें कृत्रिम उपकरण का उपयोग करके पहली अद्भुत सीमा को स्वयं व्यवस्थित करने की आवश्यकता है। तर्क की पंक्ति इस प्रकार हो सकती है: "साइन के तहत हमारे पास है, जिसका अर्थ है कि हमें भी हर में आने की आवश्यकता है"।
और यह बहुत सरलता से किया जाता है:

अर्थात्, इस मामले में हर को कृत्रिम रूप से 7 से गुणा किया जाता है और उसी सात से विभाजित किया जाता है। अब यह रिकॉर्ड एक जाना-पहचाना आकार ले चुका है।
जब कार्य हाथ से तैयार किया जाता है, तो पहली उल्लेखनीय सीमा को चिह्नित करने की सलाह दी जाती है एक साधारण पेंसिल के साथ:

क्या हुआ? वास्तव में, गोलाकार अभिव्यक्ति एक इकाई में बदल गई है और उत्पाद में गायब हो गई है:

अब केवल तीन मंजिला अंश से छुटकारा पाना बाकी है:

बहुमंजिला भिन्नों का सरलीकरण कौन भूल गया है, कृपया संदर्भ पुस्तक में सामग्री को ताज़ा करें हॉट स्कूल गणित सूत्र .

तैयार। अंतिम उत्तर:

यदि आप पेंसिल के निशान का उपयोग नहीं करना चाहते हैं, तो समाधान को इस प्रकार स्वरूपित किया जा सकता है:

“

हम पहली उल्लेखनीय सीमा का उपयोग करते हैं

“

उदाहरण 2

सीमा का पता लगाएं

फिर से हम सीमा में एक भिन्न और एक ज्या देखते हैं। हम अंश और हर में शून्य को प्रतिस्थापित करने का प्रयास करते हैं:

वास्तव में, हमारे पास अनिश्चितता है और इसलिए, हमें पहली उल्लेखनीय सीमा को व्यवस्थित करने का प्रयास करने की आवश्यकता है। सबक पर सीमाएं। समाधान उदाहरणहमने इस नियम पर विचार किया कि जब हमारे पास अनिश्चितता होती है, तो हमें अंश और हर को गुणनखंडों में विभाजित करने की आवश्यकता होती है। यहां - वही बात, हम डिग्री को एक उत्पाद (गुणक) के रूप में प्रस्तुत करेंगे:

इसी तरह पिछले उदाहरण के लिए, हम एक पेंसिल के साथ अद्भुत सीमाओं की रूपरेखा तैयार करते हैं (यहां उनमें से दो हैं), और इंगित करते हैं कि वे एक के लिए जाते हैं:

दरअसल, जवाब तैयार है:

निम्नलिखित उदाहरणों में, मैं पेंट में कला नहीं करूंगा, मुझे लगता है कि एक नोटबुक में समाधान को सही ढंग से कैसे तैयार किया जाए - आप पहले ही समझ चुके हैं।

उदाहरण 3

सीमा का पता लगाएं

हम सीमा चिह्न के तहत व्यंजक में शून्य को प्रतिस्थापित करते हैं:

एक अनिश्चितता प्राप्त हुई है जिसे प्रकट करने की आवश्यकता है। यदि सीमा में एक स्पर्शरेखा है, तो यह लगभग हमेशा प्रसिद्ध त्रिकोणमितीय सूत्र के अनुसार साइन और कोसाइन में परिवर्तित हो जाती है (वैसे, वे कोटेंजेंट के साथ भी ऐसा ही करते हैं, नीचे देखें)। विधिवत सामग्री गरम त्रिकोणमितीय सूत्र पेज पर गणितीय सूत्र, टेबल और संदर्भ सामग्री).

इस मामले में:

शून्य की कोज्या एक के बराबर है, और इससे छुटकारा पाना आसान है (यह चिह्नित करना न भूलें कि यह एक की ओर जाता है):

इस प्रकार, यदि सीमा में कोसाइन एक गुणक है, तो, मोटे तौर पर, इसे एक इकाई में बदल दिया जाना चाहिए, जो उत्पाद में गायब हो जाता है।

यहाँ सब कुछ सरल हो गया, बिना किसी गुणा और भाग के। पहली उल्लेखनीय सीमा भी एकता में बदल जाती है और उत्पाद में गायब हो जाती है:

फलतः अनंत प्राप्त होता है, ऐसा होता है।

उदाहरण 4

सीमा का पता लगाएं

हम अंश और हर में शून्य को प्रतिस्थापित करने का प्रयास करते हैं:

प्राप्त अनिश्चितता (शून्य की कोज्या, जैसा कि हमें याद है, एक के बराबर है)

हम त्रिकोणमितीय सूत्र का उपयोग करते हैं। नोट करें! किसी कारण से, इस सूत्र का उपयोग करने की सीमाएँ बहुत सामान्य हैं।

हम सीमा चिह्न से परे निरंतर गुणकों को निकालते हैं:

आइए पहली उल्लेखनीय सीमा को व्यवस्थित करें:

यहां हमारे पास केवल एक अद्भुत सीमा है, जो एक में बदल जाती है और उत्पाद में गायब हो जाती है:

आइए तीन मंजिला से छुटकारा पाएं:

सीमा वास्तव में हल हो गई है, हम इंगित करते हैं कि शेष साइन शून्य हो जाता है:

उदाहरण 5

सीमा का पता लगाएं

यह उदाहरण अधिक जटिल है, इसे स्वयं समझने का प्रयास करें:

चर को बदलकर कुछ सीमाओं को पहली उल्लेखनीय सीमा तक कम किया जा सकता है, आप इसके बारे में लेख में थोड़ी देर बाद पढ़ सकते हैं हल करने के तरीके सीमित करें.

दूसरी अद्भुत सीमा

गणितीय विश्लेषण के सिद्धांत में यह सिद्ध होता है कि:

इस तथ्य को कहा जाता है दूसरी उल्लेखनीय सीमा.

संदर्भ: एक अपरिमेय संख्या है।

न केवल एक चर एक पैरामीटर के रूप में कार्य कर सकता है, बल्कि एक जटिल कार्य भी कर सकता है। यह केवल इतना महत्वपूर्ण है कि यह अनंत के लिए प्रयास करता है.

उदाहरण 6

सीमा का पता लगाएं

जब सीमा चिह्न के तहत अभिव्यक्ति शक्ति में है - यह पहला संकेत है कि आपको दूसरी अद्भुत सीमा को लागू करने का प्रयास करने की आवश्यकता है।

लेकिन पहले, हमेशा की तरह, हम अंतहीन रूप से स्थानापन्न करने का प्रयास करते हैं बड़ी संख्याअभिव्यक्ति में, यह किस सिद्धांत द्वारा किया जाता है, पाठ में विश्लेषण किया गया था सीमाएं। समाधान उदाहरण.

यह देखना आसान है कि कब डिग्री का आधार, और घातांक - , अर्थात्, प्रपत्र की अनिश्चितता है:

यह अनिश्चितता दूसरी उल्लेखनीय सीमा की सहायता से ही प्रकट होती है। लेकिन, जैसा कि अक्सर होता है, दूसरी अद्भुत सीमा चांदी की थाली पर नहीं होती है, और इसे कृत्रिम रूप से व्यवस्थित किया जाना चाहिए। आप निम्नानुसार तर्क कर सकते हैं: इस उदाहरण में, पैरामीटर का अर्थ है कि हमें संकेतक में व्यवस्थित करने की भी आवश्यकता है। ऐसा करने के लिए, हम आधार को एक शक्ति तक बढ़ाते हैं, और ताकि अभिव्यक्ति में बदलाव न हो, हम इसे एक शक्ति तक बढ़ाते हैं:

जब कार्य हाथ से तैयार किया जाता है, तो हम एक पेंसिल से चिह्नित करते हैं:

लगभग सब कुछ तैयार है, भयानक डिग्री एक सुंदर पत्र में बदल गई है:

उसी समय, लिमिट आइकन को ही इंडिकेटर में ले जाया जाता है:

उदाहरण 7

सीमा का पता लगाएं

ध्यान! इस प्रकार की सीमा बहुत सामान्य है, कृपया इस उदाहरण का बहुत ध्यानपूर्वक अध्ययन करें।

हम सीमा चिह्न के अंतर्गत व्यंजक में एक अपरिमित रूप से बड़ी संख्या को प्रतिस्थापित करने का प्रयास करते हैं:

परिणाम एक अनिश्चितता है। लेकिन दूसरी उल्लेखनीय सीमा फॉर्म की अनिश्चितता पर लागू होती है। क्या करें? आपको डिग्री के आधार को बदलने की जरूरत है। हम इस तरह तर्क देते हैं: हमारे पास हर में, जिसका अर्थ है कि हमें अंश में व्यवस्थित करने की भी आवश्यकता है।

कई अद्भुत सीमाएँ हैं, लेकिन सबसे प्रसिद्ध पहली और दूसरी अद्भुत सीमाएँ हैं। इन सीमाओं के बारे में उल्लेखनीय बात यह है कि इनका व्यापक रूप से उपयोग किया जाता है और कई समस्याओं में आने वाली अन्य सीमाओं को खोजने के लिए उपयोग किया जा सकता है। इस पाठ के व्यावहारिक भाग में हम यही करेंगे। पहली या दूसरी उल्लेखनीय सीमा तक कम करके समस्याओं को हल करने के लिए, उनमें निहित अनिश्चितताओं का खुलासा करना आवश्यक नहीं है, क्योंकि इन सीमाओं के मूल्यों को महान गणितज्ञों द्वारा लंबे समय से घटाया गया है।

पहली उल्लेखनीय सीमारेडियन माप में व्यक्त एक ही चाप के लिए एक असीम रूप से छोटे चाप की ज्या के अनुपात की सीमा कहा जाता है:

आइए पहली उल्लेखनीय सीमा पर समस्याओं को हल करने के लिए आगे बढ़ें। नोट: यदि कोई त्रिकोणमितीय फलन सीमा चिन्ह के अंतर्गत है, तो यह लगभग निश्चित संकेत है कि इस व्यंजक को पहली उल्लेखनीय सीमा तक कम किया जा सकता है।

उदाहरण 1सीमा ज्ञात कीजिए।

समाधान। इसके बजाय प्रतिस्थापन एक्सशून्य अनिश्चितता की ओर ले जाता है:

हर एक साइन है, इसलिए, अभिव्यक्ति को पहली उल्लेखनीय सीमा तक कम किया जा सकता है। आइए परिवर्तन शुरू करें:

हर में - तीन x की ज्या, और अंश में केवल एक x होता है, जिसका अर्थ है कि आपको अंश में तीन x प्राप्त करने की आवश्यकता है। किसलिए? पेश करने के लिए 3 एक्स = एकऔर अभिव्यक्ति प्राप्त करें।

और हम पहली उल्लेखनीय सीमा के बदलाव पर आते हैं:

क्योंकि इससे कोई फर्क नहीं पड़ता कि इस सूत्र में x के बजाय कौन सा अक्षर (चर) है।

हम x को तीन से गुणा करते हैं और तुरंत विभाजित करते हैं:

विख्यात पहली उल्लेखनीय सीमा के अनुसार, हम भिन्नात्मक व्यंजक को प्रतिस्थापित करते हैं:

अब हम अंत में इस सीमा को हल कर सकते हैं:

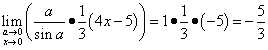उदाहरण 2सीमा ज्ञात कीजिए।

समाधान। प्रत्यक्ष प्रतिस्थापन फिर से "शून्य से शून्य विभाजन" अनिश्चितता की ओर जाता है:

पहली उल्लेखनीय सीमा प्राप्त करने के लिए, यह आवश्यक है कि अंश में साइन साइन के तहत x और हर में सिर्फ x समान गुणांक के साथ हो। इस गुणांक को 2 के बराबर होने दें। ऐसा करने के लिए, नीचे दिए गए x पर वर्तमान गुणांक की कल्पना करें, भिन्नों के साथ क्रिया करते हुए, हम प्राप्त करते हैं:

उदाहरण 3सीमा ज्ञात कीजिए।

समाधान। प्रतिस्थापित करते समय, हमें फिर से अनिश्चितता "शून्य से शून्य से विभाजित" मिलती है:

आप शायद पहले से ही समझते हैं कि मूल अभिव्यक्ति से आप पहली अद्भुत सीमा को पहली अद्भुत सीमा से गुणा कर सकते हैं। ऐसा करने के लिए, हम अंश में x के वर्गों और हर में साइन को समान कारकों में विघटित करते हैं, और x और साइन के लिए समान गुणांक प्राप्त करने के लिए, हम x को अंश में 3 से विभाजित करते हैं और तुरंत 3 से गुणा करें। हमें मिलता है:

उदाहरण 4सीमा ज्ञात कीजिए।

समाधान। फिर से हमें अनिश्चितता "शून्य से शून्य से विभाजित" मिलती है:

हम पहली दो उल्लेखनीय सीमाओं का अनुपात प्राप्त कर सकते हैं। हम अंश और हर दोनों को x से विभाजित करते हैं। फिर, गुणांकों के लिए ज्या और x पर संयोग करने के लिए, हम ऊपरी x को 2 से गुणा करते हैं और तुरंत 2 से विभाजित करते हैं, और निचले x को 3 से गुणा करते हैं और तुरंत 3 से विभाजित करते हैं। हमें मिलता है:

उदाहरण 5सीमा ज्ञात कीजिए।

समाधान। और फिर, "शून्य से विभाजित शून्य" की अनिश्चितता:

हम त्रिकोणमिति से याद करते हैं कि स्पर्शरेखा ज्या और कोज्या का अनुपात है, और शून्य की कोज्या एक के बराबर है। हम परिवर्तन करते हैं और प्राप्त करते हैं:

उदाहरण 6सीमा ज्ञात कीजिए।

समाधान। सीमा चिह्न के तहत त्रिकोणमितीय फ़ंक्शन फिर से पहली उल्लेखनीय सीमा को लागू करने का विचार सुझाता है। हम इसे ज्या से कोज्या के अनुपात के रूप में निरूपित करते हैं।

पहली उल्लेखनीय सीमा को निम्नलिखित समानता कहा जाता है:

\begin(समीकरण)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(समीकरण)

चूँकि $\alpha\to(0)$ के लिए हमारे पास $\sin\alpha\to(0)$ है, हम कहते हैं कि पहली उल्लेखनीय सीमा $\frac(0)(0)$ के रूप की अनिश्चितता को प्रकट करती है। सामान्यतया, सूत्र (1) में, चर $\alpha$ के बजाय, साइन साइन के तहत और हर में, कोई भी व्यंजक तब तक स्थित हो सकता है, जब तक कि दो शर्तें पूरी न हों:

साइन साइन के तहत और हर में एक साथ भाव शून्य हो जाते हैं, अर्थात। $\frac(0)(0)$ के रूप में अनिश्चितता है।
साइन साइन के नीचे और हर में भाव समान हैं।

पहली उल्लेखनीय सीमा से कोरोलरी का भी अक्सर उपयोग किया जाता है:

\begin(समीकरण) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(समीकरण) \begin(समीकरण) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(समीकरण) \शुरू(समीकरण) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(समीकरण)

इस पृष्ठ पर ग्यारह उदाहरण हल किए गए हैं। उदाहरण संख्या 1 सूत्रों के प्रमाण के लिए समर्पित है (2)-(4)। उदाहरण #2, #3, #4 और #5 में विस्तृत टिप्पणियों के साथ समाधान हैं। उदाहरण 6-10 में कम या बिना किसी टिप्पणी के समाधान होते हैं, जैसा कि पिछले उदाहरणों में विस्तृत स्पष्टीकरण दिया गया था। हल करते समय, कुछ त्रिकोणमितीय सूत्रों का उपयोग किया जाता है, जिन्हें पाया जा सकता है।

मैं ध्यान देता हूं कि $\frac (0) (0)$ की अनिश्चितता के साथ त्रिकोणमितीय कार्यों की उपस्थिति का मतलब यह नहीं है कि पहली उल्लेखनीय सीमा लागू की जानी चाहिए। कभी-कभी सरल त्रिकोणमितीय परिवर्तन पर्याप्त होते हैं - उदाहरण के लिए, देखें।

उदाहरण 1

साबित करें कि $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

ए) चूंकि $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, तब:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

चूंकि $\lim_(\alpha\to(0))\cos(0)=1$ और $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , फिर:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

बी) आइए प्रतिस्थापन $\alpha=\sin(y)$ करें। चूंकि $\sin(0)=0$, फिर $\alpha\to(0)$ की स्थिति से हमारे पास $y\to(0)$ है। इसके अलावा, शून्य का एक पड़ोस है जहां $\arcsin\alpha=\arcsin(\sin(y))=y$, इसलिए:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

समानता $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ साबित हुई है।

ग) आइए प्रतिस्थापन $\alpha=\tg(y)$ करें। चूंकि $\tg(0)=0$, शर्तें $\alpha\to(0)$ और $y\to(0)$ बराबर हैं। इसके अलावा, शून्य का एक पड़ोस है जहां $\arctg\alpha=\arctg\tg(y))=y$, इसलिए, बिंदु a के परिणामों पर निर्भर करते हुए), हमारे पास होगा:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

समानता $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ साबित होती है।

समानताएं ए), बी), सी) अक्सर पहली उल्लेखनीय सीमा के साथ उपयोग की जाती हैं।

उदाहरण #2

गणना सीमा $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( एक्स+7))$।

चूँकि $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ और $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, यानी और भिन्न का अंश और हर एक साथ शून्य हो जाता है, तो यहाँ हम $\frac(0)(0)$ के रूप की अनिश्चितता से निपट रहे हैं, अर्थात। प्रदर्शन किया। इसके अलावा, यह देखा जा सकता है कि साइन साइन के तहत और हर में भाव समान हैं (यानी, और संतुष्ट हैं):

तो, पृष्ठ की शुरुआत में सूचीबद्ध दोनों शर्तें पूरी होती हैं। इससे यह निष्कर्ष निकलता है कि सूत्र लागू होता है, अर्थात्। $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 )) = 1 $।

उत्तर: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7)) = 1$।

उदाहरण #3

$\lim_(x\to(0))\frac(\sin(9x))(x)$ खोजें।

चूंकि $\lim_(x\to(0))\sin(9x)=0$ और $\lim_(x\to(0))x=0$, हम फॉर्म की अनिश्चितता से निपट रहे हैं $\frac( 0 )(0)$, यानी, प्रदर्शन किया। हालांकि, साइन साइन के तहत और हर में भाव मेल नहीं खाते। यहां हर में व्यंजक को वांछित रूप में समायोजित करना आवश्यक है। हर में होने के लिए हमें व्यंजक $9x$ की आवश्यकता है - तब यह सत्य हो जाएगा। मूल रूप से, हम हर में $9$ का कारक खो रहे हैं, जिसे दर्ज करना इतना कठिन नहीं है, बस हर में व्यंजक को $9$ से गुणा करें। स्वाभाविक रूप से, $9$ से गुणा के लिए क्षतिपूर्ति करने के लिए, आपको तुरंत $9$ से विभाजित करना होगा और विभाजित करना होगा:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin) (9x))(9x) $$

अब हर और साइन साइन के तहत भाव समान हैं। $\lim_(x\to(0))\frac(\sin(9x))(9x)$ की सीमा के लिए दोनों शर्तें संतुष्ट हैं। इसलिए $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$। और इसका मतलब है कि:

$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

उत्तर: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

उदाहरण #4

$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$ खोजें।

चूंकि $\lim_(x\to(0))\sin(5x)=0$ और $\lim_(x\to(0))\tg(8x)=0$, यहां हम एक अनिश्चितता के साथ काम कर रहे हैं फॉर्म $\frac(0)(0)$. हालांकि, पहली उल्लेखनीय सीमा का रूप टूट गया है। $\sin(5x)$ वाले अंश को हर में $5x$ की आवश्यकता होती है। इस स्थिति में, सबसे आसान तरीका है कि अंश को $5x$ से विभाजित किया जाए, और तुरंत $5x$ से गुणा किया जाए। इसके अलावा, हम हर के साथ एक समान ऑपरेशन करेंगे, $\tg(8x)$ को $8x$ से गुणा और विभाजित करेंगे:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

$x$ से कम करने और निरंतर $\frac(5)(8)$ को सीमा चिह्न से बाहर निकालने पर, हम प्राप्त करते हैं:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

ध्यान दें कि $\lim_(x\to(0))\frac(\sin(5x))(5x)$ पहली उल्लेखनीय सीमा के लिए आवश्यकताओं को पूरी तरह से संतुष्ट करता है। $\lim_(x\to(0))\frac(\tg(8x))(8x)$ खोजने के लिए निम्नलिखित सूत्र लागू होता है:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to) (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8)। $$

उत्तर: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$।

उदाहरण #5

$\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$ खोजें।

चूंकि $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (याद रखें कि $\cos(0)=1$) और $\ lim_(x\to(0))x^2=0$, तो हम $\frac(0)(0)$ फॉर्म की अनिश्चितता से निपट रहे हैं। हालांकि, पहली अद्भुत सीमा को लागू करने के लिए, आपको साइन (सूत्र को लागू करने के लिए) या स्पर्शरेखा (फिर सूत्र लागू करने के लिए) पर जाकर अंश में कोसाइन से छुटकारा पाना चाहिए। आप इसे निम्न परिवर्तन के साथ कर सकते हैं:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$

आइए सीमा पर वापस जाएं:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$

अंश $\frac(\sin^2(5x))(x^2)$ पहले उल्लेखनीय सीमा के लिए आवश्यक फॉर्म के करीब है। आइए अंश $\frac(\sin^2(5x))(x^2)$ के साथ थोड़ा काम करें, इसे पहली अद्भुत सीमा में समायोजित करें (ध्यान दें कि अंश में और साइन के नीचे के भाव मेल खाने चाहिए):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$

आइए विचार की गई सीमा पर लौटते हैं:

$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\बाएं(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$

उत्तर: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

उदाहरण #6

सीमा ज्ञात कीजिए $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$।

चूंकि $\lim_(x\to(0))(1-\cos(6x))=0$ और $\lim_(x\to(0))(1-\cos(2x))=0$, तब हम $\frac(0)(0)$ की अनिश्चितता से निपट रहे हैं। आइए इसे पहली उल्लेखनीय सीमा की सहायता से खोलें। ऐसा करने के लिए, आइए कोज्या से ज्या की ओर चलें। चूँकि $1-\cos(2\alpha)=2\sin^2(\alpha)$, तब:

$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

में बदलना दी गई सीमासाइन के लिए, हमारे पास होगा:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x) \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$

उत्तर: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

उदाहरण #7

सीमा की गणना करें $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ दिए गए $\alpha\neq\ beta $.

विस्तृत स्पष्टीकरण पहले दिया गया था, लेकिन यहां हम केवल ध्यान दें कि फिर से $\frac(0)(0)$ की अनिश्चितता है। आइए सूत्र का उपयोग करके कोज्या से ज्या की ओर चलते हैं

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

उपरोक्त सूत्र का उपयोग करते हुए, हम प्राप्त करते हैं:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\दाएं| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ बीटा(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta) )(2)\दाएं)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\बाएं(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac) (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\पाप\बाएं(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\बाएं(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2)। $$

उत्तर: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ अल्फा ^ 2) (2) $।

उदाहरण #8

सीमा ज्ञात कीजिए $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$।

चूंकि $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (याद रखें कि $\sin(0)=\tg(0)=0$) और $\ lim_(x\to(0))x^3=0$, तो यहां हम $\frac(0)(0)$ फॉर्म की अनिश्चितता से निपट रहे हैं। आइए इसे इस तरह तोड़ें:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\दाएं)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2)। $$

उत्तर: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$।

उदाहरण #9

सीमा ज्ञात कीजिए $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$।

चूंकि $\lim_(x\to(3))(1-\cos(x-3))=0$ और $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, फिर $\frac(0)(0)$ के रूप की एक अनिश्चितता है। इसके विस्तार के लिए आगे बढ़ने से पहले, चर को इस तरह से बदलना सुविधाजनक है कि नया चर शून्य हो जाए (ध्यान दें कि चर $\alpha \to 0$ सूत्रों में)। चर $t=x-3$ को पेश करने का सबसे आसान तरीका है। हालांकि, आगे के परिवर्तनों की सुविधा के लिए (यह लाभ नीचे दिए गए समाधान के दौरान देखा जा सकता है), यह निम्नलिखित प्रतिस्थापन करने लायक है: $t=\frac(x-3)(2)$। मैं ध्यान देता हूं कि इस मामले में दोनों प्रतिस्थापन लागू होते हैं, केवल दूसरा प्रतिस्थापन आपको अंशों के साथ कम काम करने की अनुमति देगा। चूंकि $x\to(3)$, फिर $t\to(0)$।

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\दाएं| =\बाएं|\शुरू(गठबंधन)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin) (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

उत्तर: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$।

उदाहरण #10

सीमा खोजें $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2)$.

फिर से हम $\frac(0)(0)$ की अनिश्चितता से निपट रहे हैं। इसके विस्तार के लिए आगे बढ़ने से पहले, एक चर परिवर्तन इस तरह से करना सुविधाजनक है कि नया चर शून्य हो जाए (ध्यान दें कि सूत्रों में चर $\alpha\to(0)$) है। चर $t=\frac(\pi)(2)-x$ को पेश करने का सबसे आसान तरीका है। चूंकि $x\to\frac(\pi)(2)$, फिर $t\to(0)$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\बाएं|\फ्रैक(0)(0)\दाएं| =\बाएं|\शुरू(गठबंधन)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\बाएं(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2)। $$

उत्तर: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.

उदाहरण #11

सीमा खोजें $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

इस मामले में, हमें पहली अद्भुत सीमा का उपयोग करने की आवश्यकता नहीं है। कृपया ध्यान दें: पहली और दूसरी दोनों सीमाओं में, केवल त्रिकोणमितीय फलन और संख्याएँ हैं। अक्सर, इस प्रकार के उदाहरणों में, सीमा चिह्न के नीचे स्थित व्यंजक को सरल बनाना संभव होता है। इस मामले में, उल्लिखित सरलीकरण और कुछ कारकों में कमी के बाद, अनिश्चितता गायब हो जाती है। मैंने यह उदाहरण केवल एक उद्देश्य से दिया है: यह दिखाने के लिए कि सीमा चिह्न के तहत त्रिकोणमितीय कार्यों की उपस्थिति का मतलब पहली उल्लेखनीय सीमा के आवेदन से नहीं है।

चूंकि $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (याद रखें कि $\sin\frac(\pi)(2)=1$ ) और $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (याद रखें कि $\cos\frac(\pi)(2)=0$), तो हम अनिश्चितता से निपट रहे हैं $\frac(0)(0)$ के रूप में। हालांकि, इसका मतलब यह बिल्कुल नहीं है कि हमें पहली उल्लेखनीय सीमा का उपयोग करने की आवश्यकता है। अनिश्चितता को प्रकट करने के लिए, यह ध्यान रखना पर्याप्त है कि $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2)। $$

डेमिडोविच की समाधान पुस्तक (संख्या 475) में एक समान समाधान है। दूसरी सीमा के लिए, जैसा कि इस खंड के पिछले उदाहरणों में है, हमारे पास $\frac(0)(0)$ के रूप की अनिश्चितता है। यह क्यों उठता है? यह इसलिए उत्पन्न होता है क्योंकि $\tg\frac(2\pi)(3)=-\sqrt(3)$ और $2\cos\frac(2\pi)(3)=-1$। हम इन मानों का उपयोग अंश और हर में भावों को बदलने के लिए करते हैं। हमारे कार्यों का उद्देश्य: अंश और हर में योग को उत्पाद के रूप में लिखें। वैसे, एक चर को एक समान रूप में बदलना अक्सर सुविधाजनक होता है ताकि नया चर शून्य हो जाए (उदाहरण के लिए, इस पृष्ठ पर उदाहरण संख्या 9 या संख्या 10 देखें)। हालांकि, इस उदाहरण में, चर को बदलने का कोई मतलब नहीं है, हालांकि यदि वांछित है तो चर $t=x-\frac(2\pi)(3)$ के प्रतिस्थापन को लागू करना आसान है।

$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right) )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin) \बाएं(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac(x+\frac) (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4 .) )(\sqrt(3))। $$

जैसा कि आप देख सकते हैं, हमें पहली अद्भुत सीमा लागू करने की आवश्यकता नहीं थी। बेशक, यह वांछित होने पर किया जा सकता है (नीचे नोट देखें), लेकिन यह आवश्यक नहीं है।

पहली उल्लेखनीय सीमा का उपयोग करके समाधान क्या होगा? छिपा हुया दिखाओ

पहली उल्लेखनीय सीमा का उपयोग करते हुए, हम प्राप्त करते हैं:

$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi) )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ दाएं))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\बाएं(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3))। $$

उत्तर: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.