Вирішувати завдання з еге. Підготовка до ЄДІ з математики (профільний рівень): завдання, рішення та пояснення

Відеокурс «Отримай п'ятірку» включає всі теми, необхідні для успішної здачі ЄДІз математики на 60-65 балів. Повністю всі завдання 1-13 Профільного ЄДІ з математики. Підходить також для здачі Базового ЄДІ з математики. Якщо ви хочете здати ЄДІ на 90-100 балів, вам треба вирішувати частину 1 за 30 хвилин і без помилок!

Курс підготовки до ЄДІ для 10-11 класів, а також для викладачів. Все необхідне, щоб вирішити частину 1 ЄДІ з математики (перші 12 завдань) та задачу 13 (тригонометрія). А це понад 70 балів на ЄДІ, і без них не обійтись ні стобальнику, ні гуманітарію.

Уся необхідна теорія. Швидкі способирішення, пастки та секрети ЄДІ. Розібрано всі актуальні завдання частини 1 із Банку завдань ФІПД. Курс повністю відповідає вимогам ЄДІ-2018.

Курс містить 5 великих тем, по 2,5 години кожна. Кожна тема дається з нуля, це просто і зрозуміло.

Сотні завдань ЄДІ. Текстові завдання та теорія ймовірностей. Прості і легко запам'ятовуються алгоритми розв'язання задач. Геометрія. Теорія, довідковий матеріал, аналіз всіх типів завдань ЄДІ. Стереометрія. Хитрі прийоми розв'язання, корисні шпаргалки, розвиток просторової уяви. Тригонометрія з нуля - до завдання 13. Розуміння замість зубріння. Наочне пояснення складних понять. Алгебра. Коріння, ступеня та логарифми, функція та похідна. База на вирішення складних завдань 2 частини ЄДІ.

На ЄДІ з математики профільного рівня у 2019 р. жодних змін немає – програму іспиту, як і в минулі роки, складено з матеріалів основних математичних дисциплін. У квитках будуть присутні і математичні, і геометричні, і завдання алгебри.

Змін в КІМ ЄДІ 2019 з математики профільного рівня немає.

Особливості завдань ЄДІ з математики-2019

Здійснюючи підготовку до ЄДІ з математики (профільної), зверніть увагу на основні вимоги екзаменаційної програми. Вона покликана перевірити знання поглибленої програми: векторні та математичні моделі, функції та логарифми, алгебраїчні рівняннята нерівності.
Окремо потренуйтеся вирішувати завдання з .
Важливо виявити нестандартність мислення.

Структура іспиту

Завдання ЄДІпрофільної математикирозділені на два блоки.

Частина - короткі відповіді, включає 8 завдань, що перевіряють базову математичну підготовку та вміння застосовувати знання з математики у повсякденності.
Частина -короткі та розгорнуті відповіді. Складається з 11 завдань, 4 з яких вимагають короткої відповіді, та 7 – розгорнутої з аргументацією виконаних дій.

Підвищеної складності- Завдання 9-17 другої частини КІМу.
Високого рівня складності- Завдання 18-19 -. Ця частина екзаменаційних завдань перевіряє не лише рівень математичних знань, а й наявність чи відсутність творчого підходу до вирішення сухих «циферних» завдань, а також ефективність уміння використовувати знання та навички як професійний інструмент.

Важливо!Тому при підготовці до ЄДІ теоріюз математики завжди підкріплюйте рішенням практичних завдань.

Як розподілятимуть бали

Завдання частини першої КІМів з математики близькі до тестам ЄДІбазового рівня, тому високого бала ними набрати неможливо.

Бали за кожне завдання з математики профільного рівня розподілилися так:

за правильні відповіді завдання №1-12 – по 1 балу;
№13-15 – по 2;
№16-17 – по 3;
№18-19 – по 4.

Тривалість іспиту та правила поведінки на ЄДІ

Для виконання екзаменаційної роботи -2019 учневі відведено 3 години 55 хвилин(235 хвилин).

У цей час учень не винен:

вести себе галасливо;
використовувати гаджети та інші технічні засоби;
списувати;
намагатися допомагати іншим або просити допомоги для себе.

За подібні дії того, хто екзаменується, можуть видворити з аудиторії.

на державний іспитз математики дозволено приноситиіз собою лише лінійку, решту матеріалів видадуть безпосередньо перед ЄДІ. видаються дома.

Ефективна підготовка – це рішення онлайн тестівз математики 2019. Вибирай та отримуй максимальний бал!

Середня загальна освіта

Лінія УМК Г. К. Муравіна. Алгебра та початки математичного аналізу(10-11) (поглиб.)

Лінія УМК Мерзляк. Алгебра та початки аналізу (10-11) (У)

Математика

Підготовка до ЄДІ з математики (профільний рівень): завдання, рішення та пояснення

Розбираємо завдання та вирішуємо приклади з учителем

Екзаменаційна роботапрофільного рівня триває 3 години 55 хвилин (235 хвилин).

Мінімальний поріг– 27 балів.

Екзаменаційна робота складається з двох частин, які різняться за змістом, складністю та кількістю завдань.

Визначальною ознакою кожної частини роботи є форма завдань:

частина 1 містить 8 завдань (завдання 1-8) з короткою відповіддю у вигляді цілого числа або кінцевого десяткового дробу;
частина 2 містить 4 завдання (завдання 9-12) з короткою відповіддю у вигляді цілого числа або кінцевого десяткового дробу та 7 завдань (завдання 13–19) з розгорнутою відповіддю (повний запис рішення з обґрунтуванням виконаних дій).

Панова Світлана Анатоліївна, вчитель математики вищої категорії школи, стаж роботи 20 років:

«Для того, щоб отримати шкільний атестат, випускнику необхідно скласти два обов'язкові іспити у формі ЄДІ, один з яких математика. Відповідно до Концепції розвитку математичної освіти у Російської ФедераціїЄДІ з математики поділено на два рівні: базовий та профільний. Сьогодні ми розглянемо варіанти профільного рівня.

Завдання №1- перевіряє в учасників ЄДІ уміння застосовувати навички, отримані у курсі 5 - 9 класів з елементарної математики, у практичній діяльності. Учасник повинен володіти обчислювальними навичками, вміти працювати з раціональними числами, вміти округляти десяткові дроби, вміти переводити одні одиниці виміру до інших.

приклад 1.У квартирі, де мешкає Петро, встановили прилад обліку витрати холодної води(лічильник). Першого травня лічильник показував витрати 172 куб. м води, а першого червня – 177 куб. м. Яку суму має заплатити Петро за холодну воду за травень, якщо ціна 1 куб. м холодної води становить 34 руб 17 коп. Відповідь дайте у рублях.

Рішення:

1) Знайдемо кількість витраченої води за місяць:

177 – 172 = 5 (куб м)

2) Знайдемо скільки грошей заплатять за витрачену воду:

34,17 · 5 = 170,85 (руб)

Відповідь: 170,85.

Завдання №2-є одним із найпростіших завдань іспиту. З нею успішно справляється більшість випускників, що свідчить про володіння визначенням поняття функції. Тип завдання № 2 за кодифікатором вимог - це завдання на використання набутих знань та умінь у практичній діяльності та повсякденному житті. Завдання № 2 складається з опису за допомогою функцій різних реальних залежностей між величинами та інтерпретація їх графіків. Завдання № 2 перевіряє вміння отримувати інформацію, подану у таблицях, на діаграмах, графіках. Випускникам потрібно вміти визначати значення функції за значенням аргументу при різних способахзавдання функції та описувати поведінку та властивості функції за її графіком. Також необхідно вміти знаходити за графіком функції найбільше або найменше значеннята будувати графіки вивчених функцій. Допустимі помилки носять випадковий характер у читанні умови завдання, читанні діаграми.

#ADVERTISING_INSERT#

приклад 2.На малюнку показано зміну біржової вартості однієї акції видобувної компанії у першій половині квітня 2017 року. 7 квітня бізнесмен придбав 1000 акцій цієї компанії. 10 квітня він продав три чверті куплених акцій, а 13 квітня продав всі, що залишилися. Скільки втратив бізнесмен унаслідок цих операцій?

Рішення:

2) 1000 · 3/4 = 750 (акцій) - становлять 3/4 від усіх куплених акцій.

6) 247500 + 77500 = 325000 (крб) – бізнесмен отримав після продажу 1000 акцій.

7) 340000 – 325000 = 15000 (крб) - втратив підприємець у всіх операцій.

Відповідь: 15000.

Завдання №3- є завданням базового рівня першої частини, перевіряє вміння виконувати дії геометричними фігурамиза змістом курсу "Планіметрія". У завданні 3 перевіряється вміння обчислювати площу фігури на папері, вміння обчислювати градусні заходи кутів, обчислювати периметри і т.п.

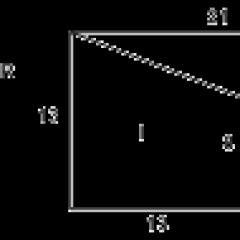
приклад 3.Знайдіть площу прямокутника, зображеного на картатому папері з розміром клітини 1 см на 1 см (див. рис.). Відповідь дайте у квадратних сантиметрах.

Рішення:Для обчислення площі цієї фігури можна скористатися формулою Піка:

Для обчислення площі даного прямокутника скористаємося формулою Піка:

S= В +	Г
	2

де В = 10, Г = 6, тому

S = 18 +	6
	2

Відповідь: 20.

Читайте також: ЄДІ з фізики: розв'язання задач про коливання

Завдання №4- завдання курсу «Теорія ймовірностей та статистика». Перевіряється вміння обчислювати ймовірність події у найпростішій ситуації.

приклад 4.На колі відзначено 5 червоних та 1 синю крапку. Визначте, яких багатокутників більше: тих, у яких усі вершини червоні, або тих, у яких одна з вершин синя. У відповіді вкажіть, скільки одних більше, ніж інших.

Рішення: 1) Скористаємося формулою числа поєднань з nелементів по k:

у яких усі вершини червоні.

3) Один п'ятикутник, який має всі вершини червоні.

4) 10 + 5 + 1 = 16 багатокутників, у яких усі вершини червоні.

у яких вершини червоні або з однією блакитною вершиною.

8) Один шестикутник, у якого вершини червоні з однією синьою вершиною.

9) 20 + 15 + 6 + 1 = 42 багатокутники, у яких усі вершини червоні або з однією синьою вершиною.

10) 42 – 16 = 26 багатокутників, у яких використовується синя точка.

11) 26 - 16 = 10 багатокутників - на скільки багатокутників, у яких одна з вершин - синя точка, більше, ніж багатокутників, у яких всі вершини тільки червоні.

Відповідь: 10.

Завдання №5- базового рівня першої частини перевіряє вміння розв'язувати найпростіші рівняння (ірраціональні, показові, тригонометричні, логарифмічні).

Приклад 5.Розв'яжіть рівняння 2 3 + x= 0,4 · 5 3 + x .

Рішення.Розділимо обидві частини даного рівняння на 5 3 + х≠ 0, отримаємо

2 3 + x	= 0,4 або		2		3 + х	=	2	,
5 3 + х			5				5

звідки випливає, що 3 + x = 1, x = –2.

Відповідь: –2.

Завдання №6за планіметрією на знаходження геометричних величин (довжин, кутів, площ), моделювання реальних ситуацій мовою геометрії. Дослідження побудованих моделей з використанням геометричних понять та теорем. Джерелом труднощів є, як правило, незнання чи неправильне застосування необхідних теорем планіметрії.

Площа трикутника ABCдорівнює 129. DE- Середня лінія, паралельна стороні AB. Знайдіть площу трапеції ABED.

Рішення.Трикутник CDEподібний до трикутника CABпо двох кутах, тому що кут при вершині Cзагальний, кут СDEдорівнює куту CABяк відповідні кути при DE || ABсічучою AC. Так як DE- Середня лінія трикутника за умовою, то за якістю середньої лінії | DE = (1/2)AB. Отже, коефіцієнт подібності дорівнює 0,5. Площі подібних фігур відносяться як квадрат коефіцієнта подібності, тому

Отже, S ABED = S Δ ABC – S Δ CDE = 129 – 32,25 = 96,75.

Завдання №7- перевіряє застосування похідної для дослідження функції. Для успішного виконання необхідне змістовне, не формальне володіння поняттям похідної.

Приклад 7.До графіку функції y = f(x) у точці з абсцисою x 0 проведена дотична, яка перпендикулярна до прямої, що проходить через точки (4; 3) і (3; -1) цього графіка. Знайдіть f′( x 0).

Рішення. 1) Скористаємося рівнянням прямої, що проходить через дві задані точки і знайдемо рівняння прямої, що проходить через точки (4; 3) та (3; -1).

(y – y 1)(x 2 – x 1) = (x – x 1)(y 2 – y 1)

(y – 3)(3 – 4) = (x – 4)(–1 – 3)

(y – 3)(–1) = (x – 4)(–4)

–y + 3 = –4x+ 16 | · (-1)

y – 3 = 4x – 16

y = 4x- 13, де k 1 = 4.

2) Знайдемо кутовий коефіцієнт дотичної k 2 , яка перпендикулярна до прямої y = 4x- 13, де k 1 = 4, за формулою:

3) Кутовий коефіцієнт дотичної – похідна функції у точці дотику. Значить, f′( x 0) = k 2 = –0,25.

Відповідь: –0,25.

Завдання №8- перевіряє в учасників іспиту знання з елементарної стереометрії, уміння застосовувати формули знаходження площ поверхонь та обсягів фігур, двогранних кутів, порівнювати обсяги подібних фігур, вміти виконувати дії з геометричними фігурами, координатами та векторами тощо.

Об'єм куба, описаного біля сфери, дорівнює 216. Знайдіть радіус сфери.

Рішення. 1) Vкуба = a 3 (де а- Довжина ребра куба), тому

а 3 = 216

а = 3 √216

2) Так як сфера вписана в куб, значить, довжина діаметра сфери дорівнює довжині ребра куба, тому d = a, d = 6, d = 2R, R = 6: 2 = 3.

Завдання №9- вимагає від випускника навичок перетворення та спрощення алгебраїчних виразів. Завдання № 9 підвищеного рівня складності із короткою відповіддю. Завдання з розділу «Обчислення та перетворення» в ЄДІ поділяються на декілька видів:

перетворення числових раціональних виразів;

перетворення алгебраїчних виразів та дробів;

перетворення числових/літерних ірраціональних виразів;

дії зі ступенями;

перетворення логарифмічних виразів;

перетворення числових/літерних тригонометричних виразів.

Приклад 9.Обчисліть tgα, якщо відомо, що cos2α = 0,6 та

3π	< α < π.
4

Рішення. 1) Скористаємося формулою подвійного аргументу: cos2α = 2 cos 2 α – 1 та знайдемо

tg 2 α =	1	– 1 =	1	– 1 =	10	– 1 =	5	– 1 = 1	1	– 1 =	1	= 0,25.
	cos 2 α		0,8		8		4		4		4

Отже, tg 2 α = ±0,5.

3) За умовою

3π	< α < π,
4

значить, α – кут II чверті та tgα< 0, поэтому tgα = –0,5.

Відповідь: –0,5.

#ADVERTISING_INSERT# Завдання №10- перевіряє в учнів вміння використовувати набуті раннє знання та вміння у практичній діяльності та повсякденному житті. Можна сказати, що це завдання з фізики, а не з математики, але всі необхідні формули та величини наведені в умові. Завдання зводяться до рішення лінійного або квадратного рівняння, або лінійного або квадратної нерівності. Тому необхідно вміти вирішувати такі рівняння та нерівності та визначати відповідь. Відповідь має вийти у вигляді цілого числа або кінцевого десяткового дробу.

Два тіла масою m= 2 кг кожне рухаються з однаковою швидкістю v= 10 м/с під кутом 2 один до одного. Енергія (у джоулях), що виділяється при їх абсолютно непружному зіткненні визначається виразом Q = mv 2 sin 2 α. Під яким найменшим кутом 2α (у градусах) повинні рухатися тіла, щоб у результаті зіткнення виділилося не менше 50 джоулів?
Рішення.Для розв'язання задачі необхідно вирішити нерівність Q ≥ 50, на інтервалі 2α ∈ (0°; 180°).

mv 2 sin 2 α ≥ 50

2· 10 2 sin 2 α ≥ 50

200 · sin 2 α ≥ 50

Оскільки α ∈ (0°; 90°), то вирішуватимемо тільки

Зобразимо розв'язання нерівності графічно:

Оскільки за умовою α ∈ (0°; 90°), значить 30° ≤ α< 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.

Завдання №11- є типовим, але виявляється непростим учнів. Головним джерелом труднощів є побудова математичної моделі (складання рівняння). Завдання №11 перевіряє вміння вирішувати текстові завдання.

Приклад 11.На весняних канікулах 11-класник Вася мав вирішити 560 тренувальних завдань для підготовки до ЄДІ. 18 березня в останній навчальний день Вася вирішив 5 завдань. Далі щодня він вирішував на те саме кількість завдань більше у порівнянні з попереднім днем. Визначте скільки завдань Вася вирішив 2 квітня в останній день канікул.

Рішення:Позначимо a 1 = 5 – кількість завдань, які Вася вирішив 18 березня, d– щоденна кількість завдань, які розв'язує Вася, n= 16 – кількість днів з 18 березня до 2 квітня включно, S 16 = 560 - загальна кількість завдань, a 16 – кількість завдань, які Вася вирішив 2 квітня. Знаючи, що щодня Вася вирішував на одну і ту ж кількість завдань більше у порівнянні з попереднім днем, можна використовувати формули знаходження суми арифметичної прогресії:

560 = (5 + a 16) · 8,

5 + a 16 = 560: 8,

5 + a 16 = 70,

a 16 = 70 – 5

a 16 = 65.

Відповідь: 65.

Завдання №12- перевіряють в учнів вміння виконувати події з функціями, вміти застосовувати похідну до вивчення функції.

Знайти точку максимуму функції y= 10ln ( x + 9) – 10x + 1.

Рішення: 1) Знайдемо область визначення функції: x + 9 > 0, x> –9, тобто x ∈ (–9; ∞).

2) Знайдемо похідну функції:

4) Знайдена точка належить проміжку (–9; ∞). Визначимо знаки похідної функції та зобразимо на малюнку поведінку функції:

Шукана точка максимуму x = –8.

Скачати безкоштовно робочу програму з математики до лінії УМК Г.К. Муравіна, К.С. Муравіна, О.В. Муравиною 10-11 Скачати безкоштовно методичні посібники з алгебри

Завдання №13-Підвищеного рівня складності з розгорнутою відповіддю, що перевіряє вміння вирішувати рівняння, що найбільш успішно розв'язується серед завдань з розгорнутою відповіддю підвищеного рівня складності.

а) Розв'яжіть рівняння 2log 3 2 (2cos x) – 5log 3 (2cos x) + 2 = 0

б) Знайдіть усі корені цього рівняння, що належать відрізку .

Рішення:а) Нехай log 3 (2cos x) = tтоді 2 t 2 – 5t + 2 = 0,

log 3 (2cos x) =	2	⇔	2cos x = 9	⇔	cos x =	4,5	⇔ т.к. \|cos x\| ≤ 1,

log 3 (2cos x) =	1		2cos x = √3		cos x =	√3
	2					2

то cos x =	√3
	2

x =	π	+ 2π k
	6

x = –	π	+ 2π k, k ∈ Z
	6

б) Знайдемо коріння, що лежить на відрізку.

З малюнка видно, що заданому відрізку належить коріння

11π	і	13π	.
6		6

Відповідь:а)	π	+ 2π k; –	π	+ 2π k, k ∈ Z; б)	11π	;	13π	.
	6		6		6		6

Завдання №14-Підвищеного рівня відноситься до завдань другої частини з розгорнутою відповіддю. Завдання перевіряє вміння виконувати події з геометричними фігурами. Завдання містить два пункти. У першому пункті завдання потрібно довести, а другому пункті обчислити.

Діаметр кола основи циліндра дорівнює 20, що утворює циліндра дорівнює 28. Площина перетинає його основи по хордах довжини 12 і 16. Відстань між хордами дорівнює 2√197.

а) Доведіть, що центри основ циліндра лежать по одну сторону від цієї площини.

б) Знайдіть кут між цією площиною та площиною основи циліндра.

Рішення:а) Хорда довжиною 12 знаходиться на відстані = 8 від центру кола основи, а хорда довжиною 16, аналогічно, – на відстані 6. Тому відстань між їх проекціями на площину, паралельну основам циліндрів, становить або 8 + 6 = 14, або 8 − 6 = 2.

Тоді відстань між хордами складає або

= = √980 = = 2√245

= = √788 = = 2√197.

За умовою реалізувався другий випадок, у ньому проекції хорд лежать з одного боку від осі циліндра. Значить, вісь не перетинає цю площину в межах циліндра, тобто основи лежать по одну сторону від неї. Що потрібно було довести.

б) Позначимо центри підстав за О1 і О2. Проведемо з центру основи з хордою довжини 12 серединний перпендикулярдо цієї хорди (він має довжину 8, як зазначалося) і з центру іншого підстави - до іншої хорді. Вони лежать в одній площині, перпендикулярній цим хордам. Назвемо середину меншої хорди B, більшої A та проекцію A на другу основу – H (H ∈ β). Тоді AB,AH ∈ β і означає, AB,AH перпендикулярні хорді, тобто прямий перетин основи з даною площиною.

Отже, шуканий кут дорівнює

∠ABH = arctg	AH	= arctg	28	= arctg14.
	BH		8 – 6

Завдання №15- підвищеного рівня складності з розгорнутою відповіддю, перевіряє вміння вирішувати нерівності, що найбільш успішно вирішується серед завдань з розгорнутою відповіддю підвищеного рівня складності.

приклад 15.Розв'яжіть нерівність | x 2 – 3x| · log 2 ( x + 1) ≤ 3x – x 2 .

Рішення:Областю визначення цієї нерівності є інтервал (–1; +∞). Розглянь окремо три випадки:

1) Нехай x 2 – 3x= 0, тобто. х= 0 або х= 3. У цьому випадку ця нерівність перетворюється на правильну, отже, ці значення входять у розв'язання.

2) Нехай тепер x 2 – 3x> 0, тобто. x∈ (–1; 0) ∪ (3; +∞). При цьому цю нерівність можна переписати у вигляді ( x 2 – 3x) · log 2 ( x + 1) ≤ 3x – x 2 і розділити на позитивний вираз x 2 – 3x. Отримаємо log 2 ( x + 1) ≤ –1, x + 1 ≤ 2 –1 , x≤ 0,5 –1 або x≤ -0,5. Враховуючи область визначення, маємо x ∈ (–1; –0,5].

3) Нарешті, розглянемо x 2 – 3x < 0, при этом x∈ (0; 3). При цьому вихідна нерівність перепишеться у вигляді (3 x – x 2) · log 2 ( x + 1) ≤ 3x – x 2 . Після поділу на позитивний вираз 3 x – x 2 отримаємо log 2 ( x + 1) ≤ 1, x + 1 ≤ 2, x≤ 1. Враховуючи область, маємо x ∈ (0; 1].

Об'єднуючи отримані рішення, отримуємо x ∈ (–1; –0.5] ∪ ∪ {3}.

Відповідь: (–1; –0.5] ∪ ∪ {3}.

Завдання №16- підвищеного рівня відноситься до завдань другої частини з розгорнутою відповіддю. Завдання перевіряє вміння виконувати дії з геометричними фігурами, координатами та векторами. Завдання містить два пункти. У першому пункті завдання потрібно довести, а другому пункті обчислити.

У рівнобедреному трикутнику ABC з кутом 120° при вершині A проведена бісектриса BD. У трикутник ABC вписано прямокутник DEFH так, що сторона FH лежить на відрізку BC, а вершина E – на відрізку AB. а) Доведіть, що FH = 2DH. б) Знайдіть площу прямокутника DEFH, якщо AB = 4.

Рішення:а)

1) ΔBEF – прямокутний, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тоді EF = BE за властивістю катета, що лежить проти кута 30°.

2) Нехай EF = DH = xтоді BE = 2 x, BF = x√3 за теоремою Піфагора.

3) Оскільки ΔABC рівнобедрений, значить, ∠B = ∠C = 30˚.

BD – бісектриса ∠B, значить ∠ABD = ∠DBC = 15˚.

4) Розглянемо ΔDBH – прямокутний, тому що. DH⊥BC.

2x	=	4 – 2x
2x(√3 + 1)	=	4

1	=	2 – x
√3 + 1	=	2

√3 – 1 = 2 – x

x = 3 – √3

EF = 3 – √3

2) S DEFH = ED · EF = (3 – √3) · 2(3 – √3)

S DEFH = 24 - 12√3.

Відповідь: 24 – 12√3.

Завдання №17- завдання з розгорнутою відповіддю, це завдання перевіряє застосування знань та умінь у практичній діяльності та повсякденному житті, уміння будувати та досліджувати математичні моделі. Це завдання - текстове завдання з економічним змістом.

Приклад 17Вклад у розмірі 20 млн. рублів планується відкрити на чотири роки. Наприкінці кожного року банк збільшує внесок на 10%, порівняно з його розміром на початку року. Крім того, на початку третього та четвертого років вкладник щороку поповнює вклад на хмлн. рублів, де х - цілечисло. Знайдіть найбільше значення х, при якому банк за чотири роки нарахує на вклад менше 17 млн. рублів.

Рішення:Наприкінці першого року вклад складе 20 + 20 · 0,1 = 22 млн рублів, а наприкінці другого - 22 + 22 · 0,1 = 24,2 млн рублів. На початку третього року вклад (у млн рублів) складе (24,2+) х), а наприкінці - (24,2+ х) + (24,2 + х)· 0,1 = (26,62 + 1,1 х). На початку четвертого року вклад складе (26,62 + 2,1 х), а наприкінці - (26,62 + 2,1 х) + (26,62 + 2,1х) · 0,1 = (29,282 + 2,31 х). За умовою, потрібно знайти найбільше ціле х, для якого виконано нерівність

(29,282 + 2,31x) – 20 – 2x < 17

29,282 + 2,31x – 20 – 2x < 17

0,31x < 17 + 20 – 29,282

0,31x < 7,718

x <	7718
	310

x <	3859
	155

x < 24	139
	155

Найбільше вирішення цієї нерівності - число 24.

Відповідь: 24.

Завдання №18- Завдання підвищеного рівня складності з розгорнутою відповіддю. Це завдання призначене для конкурсного відбору до вузів із підвищеними вимогами до математичної підготовки абітурієнтів. Завдання високого рівняскладності - це завдання не так на застосування одного методу рішення, але в комбінацію різних методів. Для успішного виконання завдання 18 необхідний, крім міцних математичних знань, також високий рівень математичної культури.

При яких aсистема нерівностей

	x 2 + y 2 ≤ 2ay – a 2 + 1

	y + a ≤ \|x\| – a

має рівно два рішення?

Рішення:Цю систему можна переписати у вигляді

	x 2 + (y– a) 2 ≤ 1

	y ≤ \|x\| – a

Якщо намалювати на площині безліч розв'язків першої нерівності, вийде начинка кола (з кордоном) радіуса 1 з центром у точці (0, а). Безліч рішень другої нерівності – частина площини, що лежить під графіком функції y = | x| – a, причому останній є графік функції
y = | x| , зрушений вниз на а. Рішення даної системи є перетинання безлічі рішень кожної з нерівностей.

Отже, два рішення дана система матиме лише у випадку, зображеному на рис. 1.

Крапки торкання кола з прямими і будуть двома рішеннями системи. Кожна пряма нахилена до осей під кутом 45°. Отже, трикутник PQR- Прямокутний рівнобедрений. Точка, крапка Qмає координати (0, а), а точка R– координати (0, – а). Крім того, відрізки PRі PQрівні радіусу кола, що дорівнює 1. Значить,

Qr= 2a = √2, a =	√2	.
	2

Відповідь: a =	√2	.
	2

Завдання №19- Завдання підвищеного рівня складності з розгорнутою відповіддю. Це завдання призначене для конкурсного відбору до вузів із підвищеними вимогами до математичної підготовки абітурієнтів. Завдання високого рівня складності - це завдання не так на застосування одного методу рішення, але в комбінацію різних методів. Для успішного виконання завдання 19 необхідно вміти шукати рішення, вибираючи різні підходи з числа відомих, модифікуючи вивчені методи.

Нехай Snсума пчленів арифметичної прогресії ( а п). Відомо що S n + 1 = 2n 2 – 21n – 23.

а) Вкажіть формулу п-го члена цієї прогресії

б) Знайдіть найменшу за модулем суму S n.

в) Знайдіть найменше п, при якому S nбуде квадратом цілого числа.

Рішення: а) Очевидно, що a n = S n – S n- 1 . Використовуючи цю формулу, отримуємо:

S n = S (n – 1) + 1 = 2(n – 1) 2 – 21(n – 1) – 23 = 2n 2 – 25n,

S n – 1 = S (n – 2) + 1 = 2(n – 1) 2 – 21(n – 2) – 23 = 2n 2 – 25n+ 27

значить, a n = 2n 2 – 25n – (2n 2 – 29n + 27) = 4n – 27.

Б) Так як S n = 2n 2 – 25n, то розглянемо функцію S(x) = | 2x 2 – 25x|. Її графік можна побачити малюнку.

Очевидно, що найменше значення досягається в цілих точках, розташованих найбільш близько до нулів функції. Очевидно, що це точки х= 1, х= 12 і х= 13. Оскільки, S(1) = |S 1 | = |2 – 25| = 23, S(12) = |S 12 | = | 2 · 144 - 25 · 12 | = 12, S(13) = |S 13 | = | 2 · 169 - 25 · 13 | = 13, то найменше значення дорівнює 12.

в) З попереднього пункту випливає, що Snпозитивно, починаючи з n= 13. Так як S n = 2n 2 – 25n = n(2n– 25), то очевидний випадок, коли цей вираз є повним квадратом, реалізується при n = 2n- 25, тобто при п= 25.

Залишилось перевірити значення з 13 до 25:

S 13 = 13 · 1, S 14 = 14 · 3, S 15 = 15 · 5, S 16 = 16 · 7, S 17 = 17 · 9, S 18 = 18 · 11, S 19 = 19 · 13, S 20 = 20 · 13, S 21 = 21 · 17, S 22 = 22 · 19, S 23 = 23 · 21, S 24 = 24 · 23.

Виходить, що при менших значеннях пПовний квадрат не досягається.

Відповідь:а) a n = 4n- 27; б) 12; в) 25.

________________

*З травня 2017 року об'єднана видавнича група «ДРОФА-ВЕНТАНА» входить до корпорації «Російський підручник». До корпорації також увійшли видавництво «Астрель» та цифрова освітня платформа «LECTA». Генеральним директоромпризначений Олександр Бричкін, випускник Фінансової академіїза Уряду РФ, кандидат економічних наук, керівник інноваційних проектів видавництва «ДРОФА» у сфері цифрової освіти ( електронні формипідручників, "Російська електронна школа", цифрова освітня платформа LECTA). До приходу у видавництво «ДРОФА» обіймав позицію віце-президента зі стратегічного розвитку та інвестицій видавничого холдингу «ЕКСМО-АСТ». Сьогодні видавнича корпорація «Російський підручник» має найбільший портфель підручників, включених до Федерального переліку - 485 найменувань (приблизно 40%, без урахування підручників для корекційної школи). Видавництвам корпорації належать найбільш затребувані російськими школами комплекти підручників з фізики, креслення, біології, хімії, технології, географії, астрономії - галузей знань, які необхідні розвитку виробничого потенціалу країни. У портфель корпорації входять підручники та навчальні посібникидля початкової школи, удостоєні Премії Президента в галузі освіти Це підручники та посібники з предметних областей, які необхідні розвитку науково-технічного і виробничого потенціалу Росії.

Оцінювання

двох частин, що включають 19 завдань. Частина 1 Частина 2

3 години 55 хвилин(235 хвилин).

Відповіді

Але можна зробити циркуль Калькуляторина екзамені не використовуються.

паспорт), перепусткаі капілярну або! Дозволяють братиз собою воду(у прозорій пляшці) та їжу

Екзаменаційна робота складається з двох частин, що включають 19 завдань. Частина 1містить 8 завдань базового рівня складності з короткою відповіддю. Частина 2містить 4 завдання підвищеного рівня складності з короткою відповіддю та 7 завдань високого рівня складності з розгорнутою відповіддю.

На виконання екзаменаційної роботи з математики відводиться 3 години 55 хвилин(235 хвилин).

Відповідідо завдань 1–12 записуються у вигляді цілого числа або кінцевого десяткового дробу. Числа запишіть у поля відповідей у тексті роботи, а потім перенесіть до бланку відповідей № 1, виданого на іспиті!

При виконанні роботи Ви можете скористатися , що видаються разом із роботою. Дозволяється використовувати лише лінійку, але можна зробити циркульсвоїми руками. Забороняється використовувати інструменти з нанесеними довідковими матеріалами. Калькуляторина екзамені не використовуються.

На іспиті при собі треба мати документ, що посвідчує особу ( паспорт), перепусткаі капілярну або гелеву ручку з чорним чорнилом! Дозволяють братиз собою воду(у прозорій пляшці) та їжу(фрукти, шоколадку, булочки, бутерброди), але можуть попросити залишити у коридорі.

Середня загальна освіта

Лінія УМК Г. К. Муравіна. Алгебра та початку математичного аналізу (10-11) (поглиб.)

Лінія УМК Мерзляк. Алгебра та початки аналізу (10-11) (У)

Математика

Підготовка до ЄДІ з математики (профільний рівень): завдання, рішення та пояснення

Розбираємо завдання та вирішуємо приклади з учителем

Екзаменаційна робота профільного рівня триває 3 години 55 хвилин (235 хвилин).

Мінімальний поріг– 27 балів.

Екзаменаційна робота складається з двох частин, які різняться за змістом, складністю та кількістю завдань.

Визначальною ознакою кожної частини роботи є форма завдань:

частина 1 містить 8 завдань (завдання 1-8) з короткою відповіддю у вигляді цілого числа або кінцевого десяткового дробу;
частина 2 містить 4 завдання (завдання 9-12) з короткою відповіддю у вигляді цілого числа або кінцевого десяткового дробу та 7 завдань (завдання 13–19) з розгорнутою відповіддю (повний запис рішення з обґрунтуванням виконаних дій).

Панова Світлана Анатоліївна, вчитель математики вищої категорії школи, стаж роботи 20 років:

«Для того, щоб отримати шкільний атестат, випускнику необхідно скласти два обов'язкові іспити у формі ЄДІ, один з яких математика. Відповідно до Концепції розвитку математичної освіти в Російській Федерації ЄДІ з математики поділено на два рівні: базовий та профільний. Сьогодні ми розглянемо варіанти профільного рівня.

приклад 1.У квартирі, де мешкає Петро, встановили прилад обліку витрати холодної води (лічильник). Першого травня лічильник показував витрати 172 куб. м води, а першого червня – 177 куб. м. Яку суму має заплатити Петро за холодну воду за травень, якщо ціна 1 куб. м холодної води становить 34 руб 17 коп. Відповідь дайте у рублях.

Рішення:

1) Знайдемо кількість витраченої води за місяць:

177 – 172 = 5 (куб м)

2) Знайдемо скільки грошей заплатять за витрачену воду:

34,17 · 5 = 170,85 (руб)

Відповідь: 170,85.

Завдання №2-є одним із найпростіших завдань іспиту. З нею успішно справляється більшість випускників, що свідчить про володіння визначенням поняття функції. Тип завдання № 2 за кодифікатором вимог - це завдання на використання набутих знань та умінь у практичній діяльності та повсякденному житті. Завдання № 2 складається з опису за допомогою функцій різних реальних залежностей між величинами та інтерпретація їх графіків. Завдання № 2 перевіряє вміння отримувати інформацію, подану у таблицях, на діаграмах, графіках. Випускникам потрібно вміти визначати значення функції за значенням аргументу при різних способах завдання функції та описувати поведінку та властивості функції за її графіком. Також необхідно вміти знаходити за графіком функції найбільше чи найменше значення та будувати графіки вивчених функцій. Допустимі помилки носять випадковий характер у читанні умови завдання, читанні діаграми.

#ADVERTISING_INSERT#

Рішення:

2) 1000 · 3/4 = 750 (акцій) - становлять 3/4 від усіх куплених акцій.

6) 247500 + 77500 = 325000 (крб) – бізнесмен отримав після продажу 1000 акцій.

7) 340000 – 325000 = 15000 (крб) - втратив підприємець у всіх операцій.

Відповідь: 15000.

Завдання №3- є завданням базового рівня першої частини, що перевіряє вміння виконувати дії з геометричними фігурами за змістом курсу «Планіметрія». У завданні 3 перевіряється вміння обчислювати площу фігури на папері, вміння обчислювати градусні заходи кутів, обчислювати периметри і т.п.

Рішення:Для обчислення площі цієї фігури можна скористатися формулою Піка:

Для обчислення площі даного прямокутника скористаємося формулою Піка:

S= В +	Г
	2

де В = 10, Г = 6, тому

S = 18 +	6
	2

Відповідь: 20.

Рішення: 1) Скористаємося формулою числа поєднань з nелементів по k:

у яких усі вершини червоні.

3) Один п'ятикутник, який має всі вершини червоні.

4) 10 + 5 + 1 = 16 багатокутників, у яких усі вершини червоні.

у яких вершини червоні або з однією блакитною вершиною.

8) Один шестикутник, у якого вершини червоні з однією синьою вершиною.

9) 20 + 15 + 6 + 1 = 42 багатокутники, у яких усі вершини червоні або з однією синьою вершиною.

10) 42 – 16 = 26 багатокутників, у яких використовується синя точка.

Відповідь: 10.

Приклад 5.Розв'яжіть рівняння 2 3 + x= 0,4 · 5 3 + x .

Рішення.Розділимо обидві частини даного рівняння на 5 3 + х≠ 0, отримаємо

2 3 + x	= 0,4 або		2		3 + х	=	2	,
5 3 + х			5				5

звідки випливає, що 3 + x = 1, x = –2.

Відповідь: –2.

Площа трикутника ABCдорівнює 129. DE- Середня лінія, паралельна стороні AB. Знайдіть площу трапеції ABED.

Отже, S ABED = S Δ ABC – S Δ CDE = 129 – 32,25 = 96,75.

(y – y 1)(x 2 – x 1) = (x – x 1)(y 2 – y 1)

(y – 3)(3 – 4) = (x – 4)(–1 – 3)

(y – 3)(–1) = (x – 4)(–4)

–y + 3 = –4x+ 16 | · (-1)

y – 3 = 4x – 16

y = 4x- 13, де k 1 = 4.

2) Знайдемо кутовий коефіцієнт дотичної k 2 , яка перпендикулярна до прямої y = 4x- 13, де k 1 = 4, за формулою:

3) Кутовий коефіцієнт дотичної – похідна функції у точці дотику. Значить, f′( x 0) = k 2 = –0,25.

Відповідь: –0,25.

Об'єм куба, описаного біля сфери, дорівнює 216. Знайдіть радіус сфери.

Рішення. 1) Vкуба = a 3 (де а- Довжина ребра куба), тому

а 3 = 216

а = 3 √216

перетворення числових раціональних виразів;

перетворення алгебраїчних виразів та дробів;

перетворення числових/літерних ірраціональних виразів;

дії зі ступенями;

перетворення логарифмічних виразів;

перетворення числових/літерних тригонометричних виразів.

Приклад 9.Обчисліть tgα, якщо відомо, що cos2α = 0,6 та

3π	< α < π.
4

Рішення. 1) Скористаємося формулою подвійного аргументу: cos2α = 2 cos 2 α – 1 та знайдемо

tg 2 α =	1	– 1 =	1	– 1 =	10	– 1 =	5	– 1 = 1	1	– 1 =	1	= 0,25.
	cos 2 α		0,8		8		4		4		4

Отже, tg 2 α = ±0,5.

3) За умовою

3π	< α < π,
4

значить, α – кут II чверті та tgα< 0, поэтому tgα = –0,5.

Відповідь: –0,5.

#ADVERTISING_INSERT# Завдання №10- перевіряє в учнів вміння використовувати набуті раннє знання та вміння у практичній діяльності та повсякденному житті. Можна сказати, що це завдання з фізики, а не з математики, але всі необхідні формули та величини наведені в умові. Завдання зводяться до розв'язання лінійного чи квадратного рівняння, або лінійної чи квадратної нерівності. Тому необхідно вміти вирішувати такі рівняння та нерівності та визначати відповідь. Відповідь має вийти у вигляді цілого числа або кінцевого десяткового дробу.

mv 2 sin 2 α ≥ 50

2· 10 2 sin 2 α ≥ 50

200 · sin 2 α ≥ 50

Оскільки α ∈ (0°; 90°), то вирішуватимемо тільки

Зобразимо розв'язання нерівності графічно:

Рішення:Позначимо a 1 = 5 – кількість завдань, які Вася вирішив 18 березня, d– щоденна кількість завдань, які розв'язує Вася, n= 16 – кількість днів з 18 березня до 2 квітня включно, S 16 = 560 - загальна кількість завдань, a 16 – кількість завдань, які Вася вирішив 2 квітня. Знаючи, що щодня Вася вирішував на одну й ту саму кількість завдань більше у порівнянні з попереднім днем, можна використовувати формули знаходження суми арифметичної прогресії:

560 = (5 + a 16) · 8,

5 + a 16 = 560: 8,

5 + a 16 = 70,

a 16 = 70 – 5

a 16 = 65.

Відповідь: 65.

Знайти точку максимуму функції y= 10ln ( x + 9) – 10x + 1.

Рішення: 1) Знайдемо область визначення функції: x + 9 > 0, x> –9, тобто x ∈ (–9; ∞).

2) Знайдемо похідну функції:

Шукана точка максимуму x = –8.

а) Розв'яжіть рівняння 2log 3 2 (2cos x) – 5log 3 (2cos x) + 2 = 0

б) Знайдіть усі корені цього рівняння, що належать відрізку .

Рішення:а) Нехай log 3 (2cos x) = tтоді 2 t 2 – 5t + 2 = 0,

log 3 (2cos x) =	2	⇔	2cos x = 9	⇔	cos x =	4,5	⇔ т.к. \|cos x\| ≤ 1,

log 3 (2cos x) =	1		2cos x = √3		cos x =	√3
	2					2

то cos x =	√3
	2

x =	π	+ 2π k
	6

x = –	π	+ 2π k, k ∈ Z
	6

б) Знайдемо коріння, що лежить на відрізку.

З малюнка видно, що заданому відрізку належить коріння

11π	і	13π	.
6		6

Відповідь:а)	π	+ 2π k; –	π	+ 2π k, k ∈ Z; б)	11π	;	13π	.
	6		6		6		6

а) Доведіть, що центри основ циліндра лежать по одну сторону від цієї площини.

б) Знайдіть кут між цією площиною та площиною основи циліндра.

Тоді відстань між хордами складає або

= = √980 = = 2√245

= = √788 = = 2√197.

б) Позначимо центри підстав за О1 і О2. Проведемо з центру основи з хордою довжини 12 серединний перпендикуляр до цієї хорди (він має довжину 8, як зазначалося) і з центру іншого основи - до іншої хорді. Вони лежать в одній площині, перпендикулярній цим хордам. Назвемо середину меншої хорди B, більшої A та проекцію A на другу основу – H (H ∈ β). Тоді AB,AH ∈ β і означає, AB,AH перпендикулярні хорді, тобто прямий перетин основи з даною площиною.

Отже, шуканий кут дорівнює

∠ABH = arctg	AH	= arctg	28	= arctg14.
	BH		8 – 6

приклад 15.Розв'яжіть нерівність | x 2 – 3x| · log 2 ( x + 1) ≤ 3x – x 2 .

Рішення:Областю визначення цієї нерівності є інтервал (–1; +∞). Розглянь окремо три випадки:

Об'єднуючи отримані рішення, отримуємо x ∈ (–1; –0.5] ∪ ∪ {3}.

Відповідь: (–1; –0.5] ∪ ∪ {3}.

Рішення:а)

1) ΔBEF – прямокутний, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тоді EF = BE за властивістю катета, що лежить проти кута 30°.

2) Нехай EF = DH = xтоді BE = 2 x, BF = x√3 за теоремою Піфагора.

3) Оскільки ΔABC рівнобедрений, значить, ∠B = ∠C = 30˚.

BD – бісектриса ∠B, значить ∠ABD = ∠DBC = 15˚.

4) Розглянемо ΔDBH – прямокутний, тому що. DH⊥BC.

2x	=	4 – 2x
2x(√3 + 1)	=	4

1	=	2 – x
√3 + 1	=	2

√3 – 1 = 2 – x

x = 3 – √3

EF = 3 – √3

2) S DEFH = ED · EF = (3 – √3) · 2(3 – √3)

S DEFH = 24 - 12√3.

Відповідь: 24 – 12√3.

(29,282 + 2,31x) – 20 – 2x < 17

29,282 + 2,31x – 20 – 2x < 17

0,31x < 17 + 20 – 29,282

0,31x < 7,718

x <	7718
	310

x <	3859
	155

x < 24	139
	155

Найбільше вирішення цієї нерівності - число 24.

Відповідь: 24.

Завдання №18- Завдання підвищеного рівня складності з розгорнутою відповіддю. Це завдання призначене для конкурсного відбору до вузів із підвищеними вимогами до математичної підготовки абітурієнтів. Завдання високого рівня складності - це завдання не так на застосування одного методу рішення, але в комбінацію різних методів. Для успішного виконання завдання 18 необхідний, крім міцних математичних знань, також високий рівень математичної культури.

При яких aсистема нерівностей

	x 2 + y 2 ≤ 2ay – a 2 + 1

	y + a ≤ \|x\| – a

має рівно два рішення?

Рішення:Цю систему можна переписати у вигляді

	x 2 + (y– a) 2 ≤ 1

	y ≤ \|x\| – a

Отже, два рішення дана система матиме лише у випадку, зображеному на рис. 1.

Qr= 2a = √2, a =	√2	.
	2

Відповідь: a =	√2	.
	2

Нехай Snсума пчленів арифметичної прогресії ( а п). Відомо що S n + 1 = 2n 2 – 21n – 23.

а) Вкажіть формулу п-го члена цієї прогресії

б) Знайдіть найменшу за модулем суму S n.

в) Знайдіть найменше п, при якому S nбуде квадратом цілого числа.

Рішення: а) Очевидно, що a n = S n – S n- 1 . Використовуючи цю формулу, отримуємо:

S n = S (n – 1) + 1 = 2(n – 1) 2 – 21(n – 1) – 23 = 2n 2 – 25n,

S n – 1 = S (n – 2) + 1 = 2(n – 1) 2 – 21(n – 2) – 23 = 2n 2 – 25n+ 27

значить, a n = 2n 2 – 25n – (2n 2 – 29n + 27) = 4n – 27.

Б) Так як S n = 2n 2 – 25n, то розглянемо функцію S(x) = | 2x 2 – 25x|. Її графік можна побачити малюнку.

Залишилось перевірити значення з 13 до 25:

S 13 = 13 · 1, S 14 = 14 · 3, S 15 = 15 · 5, S 16 = 16 · 7, S 17 = 17 · 9, S 18 = 18 · 11, S 19 = 19 · 13, S 20 = 20 · 13, S 21 = 21 · 17, S 22 = 22 · 19, S 23 = 23 · 21, S 24 = 24 · 23.

Виходить, що при менших значеннях пПовний квадрат не досягається.

Відповідь:а) a n = 4n- 27; б) 12; в) 25.

________________

*З травня 2017 року об'єднана видавнича група «ДРОФА-ВЕНТАНА» входить до корпорації «Російський підручник». До корпорації також увійшли видавництво «Астрель» та цифрова освітня платформа «LECTA». Генеральним директором призначено Олександра Бричкина, випускника Фінансової академії при Уряді РФ, кандидата економічних наук, керівника інноваційних проектів видавництва «ДРОФА» у сфері цифрової освіти (електронні форми підручників, «Російська електронна школа», цифрова освітня платформа LECTA). До приходу у видавництво «ДРОФА» обіймав позицію віце-президента зі стратегічного розвитку та інвестицій видавничого холдингу «ЕКСМО-АСТ». Сьогодні видавнича корпорація «Російський підручник» має найбільший портфель підручників, включених до Федерального переліку - 485 найменувань (приблизно 40%, без урахування підручників для корекційної школи). Видавництвам корпорації належать найбільш затребувані російськими школами комплекти підручників з фізики, креслення, біології, хімії, технології, географії, астрономії - галузей знань, які необхідні розвитку виробничого потенціалу країни. До портфелю корпорації входять підручники та навчальні посібники для початкової школи, удостоєні Премії Президента в галузі освіти. Це підручники та посібники з предметних областей, які необхідні розвитку науково-технічного і виробничого потенціалу Росії.