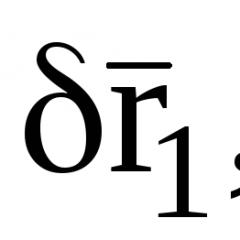Загальне рівняння динаміки. Аналітична динаміка Загальне рівняння динаміки в узагальнених координатах

Користуючись принципом Даламбера (Ч.3 Динаміка), можна надати рівнянням руху форму рівнянь рівноваги, якщо до активних (заданих) та пасивних (реакції зв'язків) сил приєднати сили інерції.

Нехай є СМТ з утримуючими та ідеальними зв'язками. Тоді для кожної МТ, що входить до СМТ, згідно з принципом Даламбер можна записати:

Повідомивши МТ, що входять до СМТ, віртуальні переміщення
, помножимо кожне з рівнянь (3.1) на відповідне
, (=1,2,…,n) і складемо отримані вирази:

.

Оскільки зв'язки, накладені на СМТ, ідеальні, виконуються умови (1.12) і з попереднього співвідношення отримуємо загальне рівняння динаміки.

Загальне рівняння динаміки – рівняння Даламбер-Лагранжа:

Під час руху СМТ з утримуючими та ідеальними зв'язками, сума елементарних робіт усіх активних сил, що діють на точки СМТ та умовно доданих до них сил інерції на будь-якому віртуальному переміщенні дорівнює нулю:

. (3.2)

Загальне рівняння динаміки можна також у вигляді:

(3.3)

Слід також зазначити, що у разі утримуючих та неідеальних зв'язків, загальне рівняння динаміки набуде вигляду:

, (3.4)

де пасивні сили – сили реакції неідеальних зв'язків.

Принцип віртуальних переміщень є окремим випадком загального рівняння динаміки (у разі рівноваги СМТ сила інерції
).

3.2. Рівняння руху смт в узагальнених координатах – рівняння Лагранжа другого роду

Із загального рівняння динаміки (співвідношення (3.2), (3.3)) можна вивести диференціальні рівняння руху СМТ в узагальнених координатах, подібно до того, як із принципу віртуальних переміщень (2.1) було виведено умови рівноваги СМТ в узагальнених координатах (2.6).

Використовуємо наступну форму загального рівняння динаміки:

.(3.5)

Нехай на СМТ, що має  ступенів свободи, накладені голономні, утримуючі та ідеальні зв'язки. Введемо на розгляд  узагальнених координат q  (=1,…,) і виразимо через них радіус-вектор -й МТ аналогічно тому, як це було представлено у формулі (1.13):

,
.

Варіюючи це співвідношення, отримаємо:

,
. (3.6)

Підставляючи співвідношення (3.6) у співвідношення (3.5) та змінюючи порядок підсумовування, маємо:

. (3.7)

Бо всі
незалежні і довільні, то рівність (3.7) може виконуватися тільки тоді, коли кожен із коефіцієнтів при дорівнює нулю, тому знаходимо:

.

Цю систему  рівнянь запишемо у вигляді:

.
(3.8)

Права частина співвідношення (3.8) є узагальненою силою (формула (1.16)) відповідну узагальненій координаті
:

.
(3.9)

Перетворимо вираз, що входить у ліву частину співвідношення (3.8) наступним чином:

(3.10)

Враховуючи, що радіус-вектор -й МТ залежить від часу t складним чином, отримаємо такий вираз для її швидкості руху:

, (3.11)

де
– називається узагальненою швидкістю ( = 1, 2,…, ).

Оскільки множники ( = 1, 2,…, ) залежать тільки від узагальнених координат і часу t (і не залежать від узагальнених швидкостей), тодиференціюючи праву та ліву частину співвідношення (3.11) по узагальненій швидкості , Приходимо до співвідношення:

. (3.12)

Знайдемо приватну похідну швидкість за узагальненою координатою , враховуючи, що узагальнені координати входять у праву частину рівності (3.11) через коефіцієнти при узагальнених швидкостях:

. (3.13)

Приватна похідна залежить від часу явно і через узагальнені координати , (
). Обчислюючи повну похідну за часом від приватної похідної, знаходимо:

. (3.14)

Порівнюючи праві частини виразів (3.13) та (3.14), помічаємо, що

. (3.15)

Повертаючись до формули (3.10) і підставляючи до неї тотожності (3.12) і (3.15), отримуємо:

.

Враховуючи що

і

наведемо останню рівність до виду:

Кінетична енергія СМТ (Ч. 3 Динаміка) визначається формулою:

,

тоді (3.16) набуде вигляду:

. (3.17)

Підставляючи вирази (3.9) та (3.17) у рівняння (3.7), отримаємо:

. (3.18)

Рівняння (3.18) єдиференціальні рівняння руху СМТ у узагальнених координатах.Ці рівняння називаютьрівняннями Лагранжа другого роду.

За наявності голономних зв'язків, накладених на систему, кількість рівнянь Лагранжа другого роду дорівнює числу незалежних узагальнених координат, тобто числу ступенів волі цієї голономної системи.

Кінетична енергія системи при підстановці у ці рівняння має бути попередньо виражена як функція узагальнених швидкостей та координат . Це буде квадратична функція узагальнених швидкостей , коефіцієнти якої можуть входити узагальнені координати (В окремих випадках кінетична енергія може бути квадратичною функцією швидкостей з постійними коефіцієнтами). Узагальнені сили також можуть бути в загальному випадку функціями узагальнених координат , та швидкостей .Таким чином, у вирази , і можуть входити узагальнені координати та їх похідні . Тому у вираз
увійдуть вже другі похідні . Отже, рівняння Лагранжа другого роду (3.18) є звичайними диференціальними рівняннями другого порядку щодо узагальнених координат
.

Основні переваги рівнянь Лагранжа другого роду (3.18) полягають у наступному. По перше, вони дають єдиний і до того ж досить простий метод вирішення завдань динаміки для будь-яких СМТ, що як завгодно рухаються, з голономними зв'язками. По-друге, число рівнянь (3.18) не залежить від числа МТ, що входять до СМТ і дорівнює числу ступенів свободи системи (у машинах, механізмах та приладах зазвичай одна, два і рідко більше двох ступенів свободи). По-третє, сили та моменти, що діють на систему, представлені тут у вигляді узагальнених сил, до яких входять тільки активні сили та моменти, а всі реакції ідеальних зв'язків автоматично виключаються з рівнянь. Цими перевагами і пояснюється широке застосування рівнянь Лагранжа другого роду в усіх технічних науках та ряді розділів фізики.

Рівняннями Лагранжа другого роду можна користуватися і у випадках, коли на систему накладені неідеальні зв'язки, наприклад, зв'язки з тертям ковзання та кочення. У цьому випадку сили та моменти неідеальних зв'язків включаються до активних сил і моментів.

Запишемо тепер рівняння (3.18) для консервативних голономних СМТ. У цьому випадку узагальнені сили можуть бути виражені через потенційну енергію СМТ:

,

і, отже, рівняння (3.17) набудуть вигляду:

,
(3.19)

Зважаючи на те, що потенційна енергія системи залежить від узагальнених координат
іне залежить від узагальнених швидкостей
, можна ще спростити вид рівняння (3.19):

.
(3.20)

Введемо поняття кінетичного потенціалу (інакше званого функцією Лагранжа):

L до = T - П,

тоді рівняння (3.20) можна написати у формі:

.
(3.21)

Рівняння (3.21) є рівняння Лагранжа другого роду для консервативних систем.

На підставі принципу Даламбер справедливі рівності:

де – активна сила; - Реакція зв'язків; - Сила інерції точки (рис. 3.36).

Помножуючи скалярно кожне із співвідношень (3.45) на можливе переміщення точки та підсумовуючи по всіх точках системи, отримаємо

(3.46)

Рівність (3.46) – загальне рівняння динаміки для механічної системи з будь-якими зв'язками. Якщо зв'язки ідеальні, то і вираз (3.46) набуває однієї з форм:

Загальне рівняння динаміки (об'єднаний принцип Даламбер-Лагранжа).У будь-який момент руху системи з ідеальними зв'язками сума елементарних робіт усіх активних сил і сил інерції точок системи дорівнюють нулю на будь-якому можливому переміщенні системи.

Узагальнені координати

Нехай система складається з Nточок та положення її визначається 3 Nкоординатами точок системи (Рис. 3.37). На систему накладено l

голономних двосторонніх зв'язків, рівняння яких s=1,2,…,l.

Таким чином, 3 Nкоординат пов'язані lрівняннями та незалежних координат буде n=3N-l.

В якості nнезалежних координат можна вибрати будь-які незалежні параметри

Незалежні параметри, що однозначно визначають положення системи, називають узагальненими координатами системи.

Мал. 3.37

Загалом вони є функціями декартових координат точок системи:

Можна висловити декартові координати через узагальнені координати:

Для радіус-вектора кожної точки системи отримаємо

Якщо зв'язки стаціонарні, то час (3.47) явно не входитиме. Для голономних зв'язків вектор можливого переміщення точки можна виразити у формі:

Якщо зв'язки голономні, число незалежних можливих переміщень (або варіацій ) збігається з числом незалежних узагальнених координат. Отже, число ступенів свободи голономної системи дорівнює числу незалежних узагальнених координат цієї системи, тобто. n=3N-l.

Для нелономних систем у загальному випадку кількість незалежних варіацій (можливих переміщень) менша за кількість узагальнених координат. Тому число ступенів свободи нелономної системи, що дорівнює кількості незалежних можливих переміщень, теж менше числа узагальнених координат системи.

Похідні узагальнених координат за часом називаються узагальненими швидкостями та позначаються

Узагальнені сили

Мал. 3.38

Визначення узагальнених сил. Розглянемо голономну систему з Nматеріальних точок, що має nступенів свободи і під дією системи сил (Рис. 3.38). Положення системи визначається nузагальненими координатами тобто.

Вектор можливого переміщення

(3.48)

Обчислимо суму елементарних робіт сил, які діють систему, на можливому переміщенні системи:

(3.49)

Підставляючи (3.48) у (3.49) та змінюючи порядок підсумовування, отримаємо

(3.50)

Скалярна величина називається узагальненою силою, віднесеною до узагальненої координати q i.

Розмірність узагальненої сили. З формули (3.50) виходить розмірність узагальненої сили [ Q]=[A]/[q]. Якщо узагальнена координата має розмірність довжини, то узагальнена сила має розмірність сили [Н], якщо узагальненою координатою є кут (розмірність – 1), то узагальнена сила має розмірність моменту сили [Н×м].

Обчислення узагальнених сил. 1. Узагальнену силу можна обчислити за формулою, що її визначає:

де F kx,F yx,F kz- Проекції сили на осі координат; x k,y yx,z k– координати точки застосування сили

2. Узагальнені сили є коефіцієнтами при відповідних варіаціях узагальнених координат у виразі для елементарної роботи (3.50):

3. Якщо системі повідомити таке можливе переміщення, при якому змінюється лише одна узагальнена координата q jто з (3.52) маємо

Індекс q iу чисельнику вказує, що сума робіт обчислюється на можливому переміщенні, при якому змінюється (варіюється) лише координата q i.

4. Для потенційних сил:

(3.53)

де – силова функція.

З виразу (3.51) з урахуванням рівностей (3.53) випливає,

Таким чином,

де потенційна енергія системи

3.5.6. Загальне рівняння динаміки у узагальнених силах.
Умови рівноваги сил

Загальне рівняння динаміки (3.50)

Вектор можливого переміщення згідно (3.48) дорівнює

З урахуванням цього виразу загальне рівняння динаміки набуває вигляду

Перетворимо його, змінивши порядок підсумовування

(3.54)

Тут – узагальнена сила активних сил, що відповідає узагальненій координаті q i; – узагальнена сила інерції, що відповідає узагальненій координаті q i.Тоді рівняння (3.54) набуває вигляду

Прирощення узагальнених координат довільні та незалежні один від одного. Тому коефіцієнти при них в останньому рівнянні повинні дорівнювати нулю:

(3.55)

Ці рівняння еквівалентні загальному рівнянню динаміки.

Якщо сили, що діють механічну систему еквівалентні нулю, тобто. механічна система рухається рівномірно прямолінійно або зберігає стан спокою, то сили інерції її точок дорівнюють нулю. Отже, узагальнені сили інерції системи дорівнюють нулю , Тоді рівняння (3.55) набувають вигляду

(3.56)

Рівності (3.56) виражають умови рівноваги сил у узагальнених силах.

У разі консервативних сил

Отже, умови рівноваги консервативної системи сил мають вигляд

Загальне рівняння динаміки системи з будь-якими зв'язками (об'єднаний принцип Даламбера-Лагранжаабо загальне рівняння механіки):

де - активна сила, прикладена до -ї точки системи; - Сила реакції зв'язків; - Сила інерції точки; - Можливе переміщення.

Воно у разі рівноваги системи при зверненні нанівець усіх сил інерції точок системи перетворюється на принцип можливих переміщень. Зазвичай його застосовують для систем із ідеальними зв'язками, для яких виконується умова

У цьому випадку (229) набуває однієї з форм:

,

,

. (230)

Таким чином, згідно з загальним рівнянням динаміки, у будь-який момент руху системи з ідеальними зв'язками сума елементарних робіт усіх активних сил і сил інерції точок системи дорівнює нулю на будь-якому можливому переміщенні системи, що допускається зв'язками.

Загального рівняння динаміки можна надати інші, еквівалентні форми. Розкриваючи скалярний добуток векторів, його можна виразити у вигляді

де – координати точки системи. З огляду на те, що проекції сил інерції на осі координат через проекції прискорень на ці осі виражаються співвідношеннями

,

загальному рівнянню динаміки можна надати форму

У цьому виді його називають загальним рівнянням динаміки в аналітичній формі.

З використанням загального рівняння динаміки необхідно вміти обчислювати елементарну роботу сил інерції системи на можливих переміщеннях. Для цього застосовуються відповідні формули елементарної роботи, отримані для звичайних сил. Розглянемо їх застосування для сил інерції твердого тіла у окремих випадках його руху.

При поступальному русі. У цьому випадку тіло має три ступені свободи і внаслідок накладених зв'язків може здійснювати лише поступальний рух. Можливі переміщення тіла, що допускають зв'язки, також є поступальними.

Сили інерції при поступальному русі призводять до рівнодіючої . Для суми елементарних робіт сил інерції на поступальному можливому переміщенні тіла отримаємо

де - Можливе переміщення центру мас і будь-якої точки тіла, так як поступальне можливе переміщення у всіх точок тіла однаково: однакові і прискорення, тобто .

При обертанні твердого тіла довкола нерухомої осі. Тіло у разі має одну ступінь свободи. Воно може обертатися навколо нерухомої осі. Можливе переміщення, яке допускається накладеними зв'язками, є поворотом тіла на елементарний кут навколо нерухомої осі.

Сили інерції, наведені до точки на осі обертання, зводяться до головного вектора і моменту . Головний вектор сил інерції прикладено до нерухомої точки, і його елементарна робота на можливому переміщенні дорівнює нулю. У головного моменту сил інерції не рівну нулю елементарну роботу здійснить лише його проекція на вісь обертання. Таким чином, для суми робіт сил інерції на можливому переміщенні маємо

,

якщо кут повідомити у напрямку дугової стрілки кутового прискорення.

При плоскому русі. Зв'язки, накладені на тверде тіло, допускають у цьому випадку лише можливе плоске переміщення. У загальному випадку воно складається з поступального можливого переміщення разом з полюсом, за який виберемо центр мас, і повороту на елементарний кут навколо осі, що проходить через центр мас і перпендикулярної площині, паралельно якій може тіло здійснювати плоский рух.

Вступ

У кінематиці розглядається опис найпростіших типів механічних рухів. При цьому не торкалися причини, що викликають зміни положення тіла щодо інших тіл, а систему відліку вибирається з міркувань зручності при вирішенні того чи іншого завдання. У динаміці, передусім, цікаві причини, внаслідок яких деякі тіла починають рухатися щодо інших тіл, і навіть чинники, що зумовлюють появи прискорення. Однак закони в механіці, строго кажучи, у різних системах відліку мають різний вигляд. Встановлено, що існують такі системи відліку, у яких закони та закономірності не залежить від вибору системи відліку. Такі системи відліку отримали назву інерційні системи(ІСО). У цих системах відліку величина прискорення залежить лише діючих сил і залежить від вибору системи відліку. Інерційною системою відліку є геліоцентрична система відліку, початок відліку якої знаходиться у центрі Сонця. Системи відліку, що рухаються рівномірно прямолінійно щодо інерційної є також інерційними, а системи відліку, що рухаються з прискоренням щодо інерційної системи, неінерційними. З цих причин поверхні землі, власне кажучи, є неінерційною системою відліку. У багатьох завдань систему відліку, пов'язану із Землею, з гарним ступенем точності можна вважати інерційною.

Основні закони динаміки в інерційних та неінерційних

Системах відліку

Здатність тіла зберігати стан рівномірного прямолінійного руху або спочиває в ІСО, називається інертністю тіла. Мірою інертності тіла є маса. Маса величина скалярна, у системі СІ вимірюється у кілограмах (кг). Мірою взаємодії є величина, яка називається силою. Сила - величина векторна, у системі СІ вимірюється в Ньютонах (Н).

Перший закон Ньютона. В інерційних системах відліку точка рухається рівномірно прямолінійно або спочиває в тому випадку, якщо сума всіх сил, що діють на неї, дорівнює нулю, тобто:

де - сили, що діють на цю точку.

Другий закон Ньютона. В інерційних системах тіло рухається з прискоренням, якщо сума всіх сил, що діють на нього не дорівнює нулю, причому добуток маси тіла на його прискорення дорівнює сумі цих сил, тобто:

Третій закон Ньютона. Сили, з якими тіла діють один на одного, рівні за величиною та протилежні за напрямом, тобто: .

Сили, як заходи взаємодії, завжди народжуються парами.

Для успішного вирішення більшості завдань із використанням законів Ньютона необхідно дотримуватися деякої послідовності дії (свого роду алгоритму).

Основні пункти алгоритму.

1. Проаналізувати умову завдання і з'ясувати, з якими тілами взаємодіє тіло, що розглядається. Виходячи з цього, визначити кількість сил, що діють на тіло, що розглядається. Припустимо, кількість сил, які діють тіло, дорівнює . Потім виконати схематично правильний малюнок, на якому побудувати всі сили, що діють тіло.

2. Використовуючи умову завдання, визначити напрямок прискорення тіла, що розглядається, і зобразити вектор прискорення на малюнку.

3. Записати у векторній формі другий закон Ньютона, тобто:

де сили, які діють тіло.

4. Вибрати інерційну систему відліку. Зобразити на малюнку прямокутну декартову систему координат, вісь якої направити по вектору прискорення, вісь ОY і ОZ направити перпендикулярно осі ОХ.

5. Скориставшись основною властивістю векторних рівностей, записати другий закон Ньютона для проекцій векторів на осі координат, тобто:

6. Якщо задачі крім сил і прискорень потрібно визначити координати і швидкість, крім другого закону Ньютона необхідно використовувати кінематичні рівняння руху. Записавши систему рівнянь, необхідно звернути увагу на те, щоб кількість рівнянь дорівнювала числу невідомих у даному завданні.

Розглянемо неінерційну систему відліку, що обертається з постійною кутовою швидкістю навколо осі, що переміщається поступово зі швидкістю щодо інерційної системи. У цьому випадку прискорення точки в інерційній системі () пов'язане з прискоренням у неінерційній системі () співвідношенням:

де - прискоренням неінерційної системи щодо інерційної системи, лінійна швидкість точки в неінерційній системі. З останнього співвідношення замість прискорення підставимо на рівність (1), отримаємо вираз:

Це співвідношення називається другим законом Ньютона у неінерційній системі відліку.

Сила інерції. Введемо позначення:

1. – поступальна сила інерції;

2. – сила Коріоліса;

3 – відцентрова сила інерції.

У задачах поступальна сила інерції зображується проти вектора прискоренням поступального руху неінерційної системи відліку (), відцентрова сила інерції від центру обертання по радіусу (); напрям сили Коріоліса визначається за правилом буравчикадля векторного добутку векторів.

Строго кажучи, сили інерції є у ​​сенсі силами, т.к. їм не виконується третій закон Ньютона, тобто. вони є парними.

Сили

Сила всесвітнього тяжіння. Сила всесвітнього тяжіння виникає в процесі взаємодії між тілами, що володіють масами, і обчислюється із співвідношення:

. (4)

Коефіцієнт пропорційності отримав назву гравітаційної постійної. Його величина у системі СІ дорівнює .

Сила реакції. Сили реакції виникають при взаємодії тіла з різними конструкціями, що обмежують його положення у просторі. Наприклад, на тіло, підвішене на нитки, діє сила реакції, яка зазвичай називається силою натягу. Сила натягу нитки спрямована завжди вздовж нитки.Формули обчислення її величини немає. Зазвичай величину її знаходять або з першого або з другого закону Ньютона. До сил реакції також відносять сили, що діють частинку на гладкій поверхні. Її називають нормальною силою реакції, позначають. Сила реакції завжди спрямована перпендикулярно даної поверхні. З боку тіла на гладку поверхню діє сила, яка називається силою нормального тиску(). За третім законом Ньютона сила реакції дорівнює за величиною силою нормального тиску, але вектори цих сил протилежні у напрямку.

Сила пружності. Сили пружності з'являються у тілах у разі, якщо тіла деформовані, тобто. якщо змінено форму тіла або його об'єм. У разі припинення деформації сили пружності зникають. Слід зауважити, що хоча сили пружності виникають при деформаціях тіл, не завжди деформація призводить до виникнення сил пружності. Сили пружності виникають у тілах, здатних відновлювати свою форму після припинення зовнішнього впливу. Такі тіла, і відповідні деформації, називаються пружними. При пластичній деформації зміни повністю зникають після припинення зовнішнього впливу. Яскравим прикладом прояви сил пружності можуть бути сили, що виникають у пружинах, схильних до деформації. Для пружних деформацій, що у деформованих тілах, сила пружності завжди пропорційна величині деформації, тобто:

, (5)

де коефіцієнт пружності (або жорсткості) пружини вектор деформації пружини.

Це твердження отримало назву закону Гука.

Сила тертя. При русі одного тіла поверхнею іншого виникають сили, що перешкоджають цьому руху. Такі сили прийнято називати силами тертя ковзання. Величина сили тертя спокою може змінюватись залежно від прикладеної зовнішньої сили. За деякого значення зовнішньої сили сила тертя спокою досягає максимального значення. Після цього починається ковзання тіла. Експериментально встановлено, що сила тертя ковзання прямо пропорційна силі нормального тиску тіла на поверхню.Згідно з третім законом Ньютона сила нормального тиску тіла на поверхню завжди дорівнює силі реакції, з якою сама поверхня діє на тіло, що рухається. З урахуванням цього формула для обчислення величини сили тертя ковзання має вигляд:

, (6)

де величина сили реакції; коефіцієнт тертя ковзання. Сила тертя ковзання, що діє на тіло, що рухається, завжди спрямована проти його швидкості, вздовж дотичних поверхонь.

Сила спротиву. При русі тіл у рідинах і газах виникають також сили тертя, але вони суттєво відрізняються від сил сухого тертя. Ці сили називаються силами в'язкого тертя, або сили опору. Сили в'язкого тертя виникають лише за відносного руху тіл. Сили опору залежить від багатьох чинників, саме: від розмірів та форми тіл, від властивостей середовища (щільності, в'язкості), від швидкості відносного руху. При малих швидкостях сила опору прямо пропорційно залежить від швидкості руху тіла щодо середовища, тобто:

. (7)

При великих швидкостях сила опору пропорційна квадрату швидкості руху тіла щодо середовища, тобто:

, (8)

де деякі коефіцієнти пропорційності, звані коефіцієнтами опору.

Основне рівняння динаміки

Основне рівняння динаміки матеріальної точки є не що інше, як математичне вираз другого закону Ньютона:

. (9)

В інерційній системі відліку до всіх сил входять лише сили, що є заходами взаємодій, в неінерційних системах у суму входять сили інерції.

З математичної точки зору співвідношення (9) є диференціальним рівнянням руху точки у векторному вигляді. Його рішення - є основне завдання динаміки матеріальної точки.

Приклади розв'язання задач

Завдання №1. На аркуш паперу поміщено склянку. З яким прискоренням треба привести в рух аркуш, щоб висмикнути його з-під склянки, якщо коефіцієнт тертя між склянкою та аркушем паперу дорівнює 0,3?

Припустимо, що з певної силі , що діє листок паперу, склянка рухається разом із листом. Зобразимо окремо сили, що діють на склянку масою. На склянку діють такі тіла: Земля із силою тяжкості , аркуш паперу із силою реакції , аркуш паперу із силою тертя , спрямованої за швидкістю руху склянки. Рух склянки є рівноприскореним, отже, вектор прискорення спрямований швидкості руху склянки.

Зобразимо вектор прискорення склянки малюнку. Запишемо другий закон Ньютона у векторній формі для сил, що діють на склянку:

.

Направимо вісь ОХ вектором прискорення склянки, а вісь OY ¾ вертикально вгору. Запишемо другий закон Ньютона у проекціях на ці осі координат, отримаємо наступні рівняння:

(1.1)

При збільшенні сили, що діє на аркуш паперу, зростає величина сили тертя, з якою аркуш паперу діє склянку. При деякому значенні сили величина сили тертя досягає свого максимального значення, що дорівнює за величиною силі тертя ковзання. З цього моменту починається ковзання склянки щодо поверхні паперу. Граничне значення сили тертя пов'язане із силою реакції, що діє на склянку таким співвідношенням:

З рівності (1.2) виражаємо величину сили реакції, а потім підставляємо останнє співвідношення, маємо . З отриманого співвідношення знаходимо величину сили тертя і поставляємо в рівність (1.1), отримаємо вираз визначення максимального прискорення склянки:

Підставивши числові значення величин в останню рівність, знайдемо величину максимального прискорення склянки:

.

Отримана величина прискорення склянки дорівнює мінімальному прискоренню аркуша паперу, у якому його можна «висмикнути» з-під склянки.

Відповідь: .

Зобразимо всі сили, які діють тіло. Крім зовнішньої сили на тіло діє Земля із силою тяжіння, горизонтальна поверхня із силою реакції та силою тертя, спрямованою проти швидкості руху тіла. Тіло рухається рівноприскорено, і, отже, вектор його прискорення спрямовано швидкості руху. Зобразимо вектор малюнку. Вибираємо систему координат так, як показано на малюнку. Записуємо другий закон Ньютона у векторній формі:

.

Використовуючи основну властивість векторних рівностей, запишемо рівняння для проекцій векторів, що входять до останньої векторної рівності:

Записуємо співвідношення для сили тертя ковзання

З рівності (2.2) знаходимо величину сили реакції

З отриманого виразу підставимо на рівність (2.3) замість величини сили реакції , отримаємо вираз

Підставивши отриманий вираз для сили тертя у рівність (2.1), матимемо формулу для обчислення прискорення тіла:

В останню формулу підставимо числові дані в системі СІ, знайдемо величину прискорення руху вантажу:

Відповідь: .

Для мінімальної величини сили визначимо напрям сили тертя, яка діє на брусок, що покоїться. Уявімо, що сила менша від тієї мінімальної сили, достатньої для того, щоб тіло залишалося у спокої. У цьому випадку тіло рухатиметься вниз, і сила тертя, прикладена до нього, буде спрямована вертикально вгору. Щоб зупинити тіло, потрібно збільшити величину прикладеної сили . Крім того, на це тіло діє Земля з силою тяжіння, спрямованою вертикально вниз, а також стінка з силою реакції, спрямованої горизонтально вліво. Зобразимо на малюнку всі сили, які діють тіло. Візьмемо прямокутну декартову систему координат, осі якої направимо так, як показано на малюнку. Для тіла, що покоїться, запишемо перший закон Ньютона у векторній формі:

.

Для знайденої векторної рівності запишемо рівні для проекцій векторів на осі координат, отримаємо наступні рівняння:

При мінімальному значенні зовнішньої сили величина сили тертя спокою досягає максимального значення, що дорівнює величині сили тертя ковзання:

З рівності (3.1) знаходимо величину сили реакції і підставляємо в рівність (3.3), отримаємо наступне вираз для сили тертя:

.

Підставимо замість сили тертя у рівність (3.2) праву частину цього співвідношення, отримаємо формулу для обчислення величини прикладеної сили:

З останньої формули знаходимо величину сили:

.

Відповідь: .

Зобразимо всі сили, що діють на кульку, що рухається в повітрі вертикально вниз. На нього діє Земля з силою тяжіння та повітря з силою опору. Зобразимо розглянуті сили малюнку. У початковий момент часу рівнодіюча всіх сил має максимальне значення, оскільки швидкість кульки дорівнює нулю і сила опору також дорівнює нулю. У цей момент кулька має максимальне прискорення, що дорівнює . У міру руху кульки швидкість його руху збільшується, отже, сила опору повітря зростає. У певний момент часу сила опору досягає величини, що дорівнює величині сили тяжіння. З цього часу кулька рухається поступово. Запишемо перший закон Ньютона у векторній формі для рівномірного руху кульки:

.

Направимо вісь OY вертикально вниз. Запишемо для даної векторної рівності рівність для векторних проекцій на вісь OY:

. (4.1)

Сила опору залежить від площі поперечного перерізу кульки та величини її швидкості руху наступним чином:

, (4.2)

де коефіцієнт пропорційності, званий коефіцієнтом опору.

З рівностей (4.1) і (4.2) випливає таке співвідношення:

. (4.3)

Виразимо масу кульки через її щільність та об'єм, а об'єм у свою чергу, - через радіус кульки:

. (4.4)

З цього виразу знаходимо масу і підставляємо в рівність (4.3), отримаємо наступну рівність:

. (4.5)

Виражаємо площу поперечного перерізу кульки через її радіус:

З урахуванням співвідношення (4.6) рівність (4.5) набуде наступного вигляду:

.

Позначимо як радіус першої кульки; як радіус другої кульки. Запишемо формули для швидкостей встановленого руху першої та другої кульок:

З отриманих рівностей знаходимо відношення швидкостей:

.

З умови завдання ставлення радіусів кульок дорівнює двом. Використовуючи цю умову, знаходимо відношення швидкостей:

.

Відповідь: .

На тіло, що рухається вгору вздовж похилої площини, діють зовнішні тіла: а) Земля із силою тяжіння, спрямованою вертикально донизу; б) похила площина із силою реакції , спрямованої перпендикулярно похилій площині; в) похила площину із силою тертя, спрямованої проти руху тіла; г) зовнішнє тіло із силою, спрямованою вгору вздовж похилої площини. Під дією цих сил тіло рухається рівноприскорено вгору похилою площиною, і, отже, вектор прискорення спрямований переміщення тіла. Зобразимо вектор прискорення малюнку. Запишемо другий закон Ньютона у векторній формі:

.

Виберемо прямокутну декартову систему координат, вісь ОХ якої направимо на прискорення руху тіла, а вісь OY - перпендикулярно похилій площині. Запишемо другий закон Ньютона у проекціях на ці осі координат, отримаємо наступні рівняння:

Сила тертя ковзання пов'язана із силою реакції наступним співвідношенням:

З рівності (5.2) знаходимо величину сили реакції і підставляємо на рівність (5.3), маємо такий вираз для сили тертя:

. (5.4)

Підставимо в рівність (5.1) замість сили тертя праву частину рівності (5.4), отримаємо наступне рівняння для обчислення величини сили, що шукається:

Обчислимо величину сили:

Відповідь: .

Зобразимо всі сили, що діють на тіла та на блок. Розглянемо процес руху тіл, пов'язаних ниткою, перекинутою через блок. Нитка є невагомою і нерозтяжною, отже, величина сили натягу будь-якому ділянці нитки буде однаковою, тобто. та .

Переміщення тіл за будь-які проміжки часу будуть однаковими, і, отже, будь-якої миті часу однаковими будуть величини швидкостей та прискорень цих тіл. З того, що блок обертається без тертя і є невагомим, випливає, що сила натягу нитки по обидва боки блоку буде однаковою, тобто: .

Звідси випливає рівність сил натягу нитки, що діє перше і друге тіло, тобто. . Зобразимо на малюнку вектори прискорень першого та другого тіла. Зобразимо дві осі ОХ. Першу вісь направимо уздовж вектора прискорення першого тіла, другу - уздовж вектора прискорення другого тіла. Запишемо другий закон Ньютона для кожного тіла у проекції на ці осі координат:

Враховуючи, що , і висловивши з першого рівняння, підставимо на друге рівняння, отримаємо

З останньої рівності знаходимо величину прискорення:

.

З рівності (1) знаходимо величину сили натягу:

Відповідь: , .

На мале кільце при його обертанні по колу діють дві сили: сила тяжіння, спрямована вертикально вниз, і сила реакції, спрямована до центру кільця. Зобразимо ці сили малюнку, і навіть покажемо у ньому траєкторію руху кільця. Вектор доцентрового прискорення кільця лежить в площині траєкторії і спрямований до осі обертання. Зобразимо малюнку. Запишемо другий закон Ньютона у векторній формі для кільця, що обертається:

.

Виберемо прямокутну систему координат, вісь ОХ якої направимо по доцентровому прискоренню , а вісь OY - вертикально вгору вздовж осі обертання. Запишемо другий закон Ньютона у проекціях на ці осі координат:

З рівності (7.2) знаходимо величину сили реакції і підставляємо на рівність (7.1), отримаємо вираз:

. (7.3)

Центрошвидке прискорення пов'язане з частотою обертання співвідношенням: де радіус обертання маленького кільця. Підставимо праву частину останньої рівності замість формули (7.3), отримаємо наступне співвідношення:

. (7.4)

З малюнка знаходимо величину тангенсу кута альфа . З урахуванням цього виразу рівність (7.4) набуде вигляду:

З останнього рівняння знаходимо шукану висоту:

Відповідь: .

На тіло, що обертається разом із диском, діють три сили: сила тяжіння, сила реакції та сила тертя, спрямована до осі обертання. Зобразимо всі сили малюнку. Покажемо на даному малюнку напрямок вектора доцентрового прискорення . Записуємо другий закон Ньютона у векторній формі:

.

Виберемо прямокутну декартову систему координат так, як показано малюнку. Запишемо другий закон Ньютона в проекціях на осі координат:

; (8.1)

. (8.2)

Запишемо співвідношення для доцентрового прискорення:

. (8.3)

Підставимо праву частину рівності (8.3) замість доцентрового прискорення до рівності (8.1), отримаємо:

. (8.4)

З рівності (8.4) видно, що величина сили тертя прямо пропорційна радіусу обертання, тому при збільшенні радіусу обертання сила тертя спокою збільшується, і при певній величині сила тертя спокою досягає максимального значення, що дорівнює силі тертя ковзання ().

З урахуванням рівності (8.2), отримаємо вирази для максимальної сили тертя спокою:

.

Підставимо праву частину отриманої рівності замість сили тертя рівність (4), отримаємо наступне співвідношення:

З цього рівняння знаходимо граничне значення радіусу обертання:

Відповідь: .

Під час польоту краплі на неї діє дві сили: сила тяжіння та сила опору. Зобразимо всі сили малюнку. Виберемо вертикально спрямовану вісь OY, початок відліку якої розташуємо лежить на Землі. Запишемо основне рівняння динаміки:

.

Спроектуємо рівність на вісь OY, матимемо співвідношення:

Розділимо обидві частини останньої рівності на і одночасно помножимо обидві частини на , врахуємо що , отримаємо вираз:

Розділимо обидві частини цього виразу на , Отримаємо співвідношення:

.

Інтегруємо останнє співвідношенням, отримуємо залежність швидкості від часу: .

Константу знайдемо з початкових умов ( ), отримаємо шукану залежність швидкості від часу:

.

Визначаємо максимальну швидкість із умови :

.

Відповідь: ; .

Зобразимо малюнку сили, що діють шайбу. Запишемо другий закон Ньютона у проекціях на осі OX, OY та OZ

Т.к. , то для всієї траєкторії руху шайби для сили тертя справедливо формула , яка, з урахуванням рівності для OZ, перетворюється на вигляд:

З урахуванням цього співвідношення рівність для осі OX набуде вигляду

Спроектуємо другий закон Ньютона на дотичну до траєкторії руху шайби в точці, що розглядається, отримаємо співвідношення:

де - Величина тангенціального прискорення. Порівнюючи праві частини останніх рівностей, робимо висновок у тому, что .

Оскільки і , то з урахуванням попереднього співвідношення маємо рівність , інтегрування якого призводить до виразу , де константа інтегрування. Підставимо останній вираз , отримаємо залежність швидкості від кута:

Константу визначимо з початкових умов (коли . ). З огляду на це запишемо остаточну залежність

.

Мінімальне значення швидкості досягається тоді, коли , вектор швидкості спрямований паралельно осі OX а її величина дорівнює .

Приклад розв'язання задачі із застосуванням загального рівняння динаміки (принцип Даламбера – Лагранжа) для системи з твердими тілами, вантажами, шківами та блоком, з'єднаних нитками.

Зміст

Умова задачі

Механічна система складається з однорідних ступінчастих шківів 1 і 2, обмотаних нитками, вантажів 3-6, прикріплених до цих ниток, і невагомого блоку. Система рухається у вертикальній площині під дією сил тяжіння та пари сил з моментом M = 10 Н·м, доданої до шківа 1. Радіуси щаблів шківа 1 рівні: R 1 = 0,2 м, r 1 = 0,1 м, а шківа 2 - R 2 = 0,3 м, r 2 = 0,15 м; їх радіуси інерції щодо осей обертання дорівнюють відповідно ρ 1 = 0,1 мта ρ 2 = 0,2 м.

Нехтуючи тертям, визначити прискорення вантажу 5. Ваги шківів та вантажів задані: P 1 = 40 Н, P 2 = 0 , P 3 = 0 , P 4 = 20 Н, P 5 = 30 Н, P 6 = 10 Н. Вантажі, ваги яких дорівнюють нулю, на кресленні не зображати.

Вказівка. При вирішенні задачі використовувати загальне рівняння динаміки (принцип Даламбера – Лагранжа).

Рішення завдання

Дано: R 1 = 0,2 м, r 1 = 0,1 м, R 2 = 0,3 м, r 2 = 0,15 м, ρ 1 = 0,1 м, ρ 2 = 0,2 м. P 1 = 40 Н, P 2 = 0 , P 3 = 0 , P 4 = 20 Н, P 5 = 30 Н, P 6 = 10 Н, M = 10 Н·м.

Знайти: a 5 .

Встановлення кінематичних співвідношень

Встановимо кінематичні співвідношення. Нехай V 4 , V 5 , V 6 , a 4 , a 5 , a 6 , δS 4 , δS 5 , δS 6 - швидкості, прискорення та малі переміщення вантажів 4,5 та 6. Нехай ω 1 , ω 2 , ε 1 , ε 2 , δφ 1 , δφ 2 - кутові швидкості, кутові прискорення та малі кути повороту шківів 1 і 2.

Швидкість руху нитки між тілами 2, 4 та 5:
. Звідси.
Швидкість руху нитки між шківами 1 і 2:
. Звідси
.
Швидкість руху нитки між тілами 1 та 6:
.

Отже ми знайшли зв'язок між швидкостями тіл.
;
;
.

Оскільки прискорення - це похідні швидкостей за часом,
то диференціюючи за часом попередні формули, знаходимо зв'язок між прискореннями:
;
;
.

Оскільки швидкості - це похідні від переміщень за часом, такий зв'язок є між нескінченно малими переміщеннями.
;
;
.

Активні зовнішні сили

Розглянемо зовнішні сили, що діють систему.
Це сили тяжіння тіл P 1 = 40 Н, P 4 = 20 Н, P 5 = 30 Нта P 6 = 10 Н, Спрямовані вниз;
задана пара сил з моментом M = 10 Н·м;
сили тиску осей N 1 , N 2 і N шківів 1, 2 та невагомого блоку;
сили реакції N 4 та N 6 , що діють на вантажі з боку поверхонь, перпендикулярні до цих поверхонь.

Сили інерції

Ми вирішуватимемо це завдання за допомогою загального рівняння динаміки, застосовуючи принцип Даламбера - Лагранжа. Він у тому, що спочатку ми вводимо сили інерції. Після введення сил інерції завдання динаміки перетворюється на завдання статики. Тобто нам потрібно знайти невідомі сили інерції, щоб система перебувала у рівновазі. Це завдання статики ми вирішуємо, застосовуючи принцип Даламбера. Тобто вважаємо, що система здійснила мале переміщення. Тоді в рівновазі сума робіт усіх сил при такому переміщенні дорівнює нулю.

Отже, на першому етапі ми вводимо сили інерції. Для цього припускаємо, що система рухається з деяким, поки що не певним, прискоренням. Тобто шківи 1 та 2 обертаються з кутовими прискореннями ε 1 та ε 2 відповідно; вантажі 4,5 і 6 здійснюють поступальний рух із прискореннями a 4 , a 5 та a 6 відповідно. Між цими прискореннями є зв'язки, які ми виявили раніше. Тобто всі ці прискорення можна виразити через одне прискорення a 5 . Сили інерції визначаються так, що вони рівні за модулем і протилежні у напрямку тих сил (і моментів сил), які, за законами динаміки, створювали б передбачувані прискорення (за відсутності інших сил).

Визначаємо модулі (абсолютні значення) сил і моментів інерції та виражаємо їх через a 5 .
Нехай – маси тіл;
- Момент інерції шківа 1.
Момент сил інерції, що діє на шків 1:
.
Сили інерції, що діють на вантажі 4, 5 та 6:
;
;
.

Зображаємо сили інерції на кресленні з огляду на те, що їхні напрямки протилежні прискоренням.

Застосування загального рівняння динаміки

Даємо системі нескінченно мале переміщення. Нехай вантаж 5 перемістився на малу відстань δS 5 . Тоді кут повороту δφ 1 шківа 1 та переміщення δS 4 та δS 6 вантажів 4 та 6 визначаються за допомогою встановлених раніше кінематичних співвідношень. Оскільки нитки нерозтяжні, то вони не роблять роботу за такого переміщення. Це означає, що система має ідеальні зв'язки. Тому ми можемо застосувати загальне рівняння динаміки:
,
згідно з яким сума робіт усіх активних сил і сил інерції, за такого переміщення, дорівнює нулю.

Визначення суми робіт зовнішніх активних сил та сил інерції

Робота, яку здійснює сила при переміщенні точки її застосування на мале усунення дорівнює скалярному добутку векторів , тобто добутку модулів векторів F і ds на косинус кута між ними.

Робота, зроблена моментом сил, обчислюється аналогічно:
.

Визначаємо роботи всіх активних сил та сил інерції. Оскільки центри осей шківів 1, 2 та невагомого блоку не здійснюють переміщень, то сили P 1 , N 1 , N 2 та N не виконують роботу. Оскільки сили N 4 та N 6 перпендикулярні переміщенням вантажів 4 і 6, ці сили також не здійснюють роботу.

Знаходимо суму робіт інших активних зусиль і сил інерції.

.
Підставляємо вирази для сил інерції та застосовуємо кінематичні співвідношення.

.
Скорочуємо на δS 5 та перетворюємо.

.
Підставляємо чисельні значення.

;
;