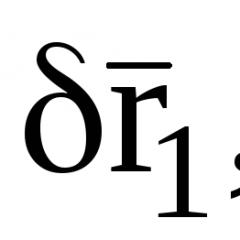معادله کلی دینامیک. دینامیک تحلیلی معادله کلی دینامیک در مختصات تعمیم یافته

با استفاده از اصل دالامبر (بخش 3 دینامیک)، می توان معادلات حرکت را شکل معادلات تعادل داد، اگر نیروهای اینرسی به نیروهای فعال (داده شده) و غیرفعال (واکنش محدودیت) اضافه شوند.

بگذارید یک SMT با اتصالات مهارکننده و ایده آل وجود داشته باشد. سپس، برای هر MT موجود در MMT، با توجه به اصل D’Alembert، می‌توانیم بنویسیم:

با اطلاع رسانی به MT های موجود در حرکات مجازی SMT
، هر یک از معادلات (3.1) را در معادله مربوطه ضرب کنید
، (=1,2,…,n) و عبارات حاصل را اضافه کنید:

.

از آنجایی که اتصالات اعمال شده بر روی MMT ایده آل هستند، پس شرایط (1.12) برآورده می شود و از رابطه قبلی معادله کلی دینامیک را به دست می آوریم.

معادله کلی دینامیک معادله d'Alembert-Lagrange است:

هنگامی که SMT با اتصالات مهار کننده و ایده آل حرکت می کند، مجموع کارهای اولیه همه نیروهای فعالی که بر روی نقاط SMT عمل می کنند و نیروهای اینرسی که به طور مشروط به آنها اعمال می شود در هر جابجایی مجازی صفر است:

. (3.2)

معادله دینامیک عمومی را می توان به صورت زیر نشان داد:

(3.3)

همچنین لازم به ذکر است که در مورد اتصالات مهار کننده و غیر ایده آل، معادله دینامیک کلی به شکل زیر خواهد بود:

, (3.4)

جایی که نیروهای منفعل - نیروهای واکنشی از اتصالات غیر ایده آل.

اصل جابجایی های مجازی یک مورد خاص از معادله عمومی دینامیک است (در مورد تعادل SMT، نیروی اینرسی
).

3.2. معادلات حرکت SMT در مختصات تعمیم یافته - معادلات لاگرانژ از نوع دوم

از معادله کلی دینامیک (روابط (3.2)، (3.3)) می توان معادلات دیفرانسیل حرکت SMT را در مختصات تعمیم یافته استخراج کرد، همانطور که شرایط تعادل SMT در مختصات تعمیم یافته (2.6) از اصل استخراج شد. جابجایی های مجازی (2.1).

ما از شکل زیر از معادله دینامیک عمومی استفاده می کنیم:

.(3.5)

اجازه دهید محدودیت‌های هولونومیک، محدودکننده و ایده‌آل بر MMT اعمال شود که دارای  درجه آزادی است. اجازه دهید  مختصات تعمیم یافته q  (=1،...،) را معرفی کنیم و از طریق آنها بردار شعاع -امین MT را به همان شکلی که در فرمول (1.13) ارائه شد بیان کنیم:

,
.

با تغییر این نسبت، دریافت می کنیم:

,
. (3.6)

با جایگزینی رابطه (3.6) به رابطه (3.5) و تغییر ترتیب جمع، داریم:

. (3.7)

از آنجایی که همه چیز
مستقل و دلخواه هستند، برابری (3.7) تنها زمانی می تواند برآورده شود که هر یک از ضرایب در برابر با صفر است پس می‌یابیم:

.

این سیستم معادلات را به شکل زیر می نویسیم:

.
(3.8)

سمت راست رابطه (3.8) نیروی تعمیم یافته را نشان می دهد (فرمول (1.16)) مربوط به مختصات تعمیم یافته است
:

.
(3.9)

اجازه دهید عبارت موجود در سمت چپ رابطه (3.8) را به صورت زیر تبدیل کنیم:

(3.10)

با توجه به اینکه بردار شعاع -امین MT به صورت پیچیده به زمان t بستگی دارد، عبارت زیر را برای سرعت حرکت آن به دست می آوریم:

, (3.11)

جایی که
– سرعت تعمیم یافته نامیده می شود ( = 1, 2,…, ).

از آنجایی که ضرب کننده ها ( = 1, 2,…, ) فقط به مختصات تعمیم یافته و زمان t بستگی دارد (و به سرعت تعمیم یافته بستگی ندارد)، که طرف راست و چپ رابطه (3.11) را با سرعت تعمیم یافته متمایز می کند. ، به رابطه می رسیم:

. (3.12)

بیایید مشتق جزئی سرعت را پیدا کنیم در امتداد یک مختصات تعمیم یافته با در نظر گرفتن اینکه مختصات تعمیم یافته از طریق ضرایب در سرعت های تعمیم یافته وارد سمت راست برابری (3.11) می شوند:

. (3.13)

مشتق جزئی به طور صریح و از طریق مختصات تعمیم یافته به زمان بستگی دارد , (
). با محاسبه کل مشتق زمانی مشتق جزئی، متوجه می شویم:

. (3.14)

با مقایسه سمت راست عبارات (3.13) و (3.14)، متوجه می شویم که

. (3.15)

با بازگشت به فرمول (3.10) و جایگزینی هویت های (3.12) و (3.15) به آن، به دست می آوریم:

.

با توجه به اینکه

و

اجازه دهید آخرین برابری را به شکل کاهش دهیم:

انرژی جنبشی SMT (بخش 3 دینامیک) با فرمول تعیین می شود:

,

سپس (3.16) به شکل زیر در می آید:

. (3.17)

با جایگزینی عبارات (3.9) و (3.17) به معادلات (3.7)، به دست می آوریم:

. (3.18)

معادلات (3.18) هستندمعادلات دیفرانسیل حرکت SMT در مختصات تعمیم یافته.این معادلات نامیده می شوندمعادلات لاگرانژ دوم به نوعی.

در حضور قیود هولونومیک اعمال شده بر سیستم، تعداد معادلات لاگرانژ نوع دوم برابر با تعداد مختصات تعمیم یافته مستقل، یعنی تعداد درجات آزادی این سیستم هولونومی است.

انرژی جنبشی سیستم، زمانی که به این معادلات جایگزین شود، ابتدا باید به عنوان تابعی از سرعت های تعمیم یافته بیان شود. و مختصات . این تابع درجه دوم سرعت های تعمیم یافته خواهد بود که ضرایب آن ممکن است شامل مختصات تعمیم یافته باشد (در موارد خاص، انرژی جنبشی می تواند تابع درجه دوم سرعت ها با ضرایب ثابت باشد). نیروهای تعمیم یافته همچنین می تواند، در حالت کلی، توابع مختصات تعمیم یافته باشد ، و سرعت .بنابراین در عبارات , و ممکن است شامل مختصات تعمیم یافته باشد و مشتقات آنها . بنابراین در بیان
مشتقات دوم شامل خواهد شد . در نتیجه، معادلات لاگرانژ از نوع دوم (3.18) معادلات دیفرانسیل معمولی مرتبه دوم با توجه به مختصات تعمیم یافته هستند.
.

مزایای اصلی معادلات لاگرانژ نوع دوم (3.18) به شرح زیر است. اولا، آنها یک روش یکپارچه و بسیار ساده برای حل مسائل دینامیک برای هر SMT خودسرانه با اتصالات هولونومیک ارائه می دهند. ثانیاً، تعداد معادلات (3.18) به تعداد MT های موجود در MMT بستگی ندارد و برابر با تعداد درجات آزادی سیستم است (در ماشین ها، مکانیزم ها و دستگاه ها معمولاً یک، دو و به ندرت بیشتر است. بیش از دو درجه آزادی). سوم، نیروها و گشتاورهای وارد بر سیستم در اینجا به صورت نیروهای تعمیم یافته ارائه می شوند که فقط شامل نیروها و گشتاورهای فعال می شود و تمام واکنش های اتصالات ایده آل به طور خودکار از معادلات حذف می شوند. این مزایا استفاده گسترده از معادلات لاگرانژ نوع دوم را در تمام علوم فنی و تعدادی از شاخه های فیزیک توضیح می دهد.

معادلات لاگرانژ نوع دوم را می‌توان در مواردی که محدودیت‌های غیر ایده‌آل بر سیستم اعمال می‌شود، به‌عنوان مثال، کوپلینگ‌هایی با اصطکاک لغزشی و غلتشی استفاده کرد. در این حالت نیروها و گشتاورهای اتصالات غیر ایده آل در تعداد نیروها و گشتاورهای فعال لحاظ می شود.

اجازه دهید اکنون معادلات (3.18) را برای SMT های هولونومیک محافظه کارانه بنویسیم. در این حالت نیروهای تعمیم یافته را می توان بر حسب انرژی پتانسیل SMT بیان کرد:

,

و بنابراین، معادلات (3.17) به شکل زیر خواهد بود:

,
(3.19)

با در نظر گرفتن اینکه انرژی پتانسیل سیستم به مختصات تعمیم یافته بستگی دارد
به سرعت های تعمیم یافته بستگی ندارد
, می‌توانیم شکل معادله (3.19) را ساده‌تر کنیم:

.
(3.20)

بیایید مفهوم پتانسیل جنبشی (که تابع لاگرانژ نامیده می شود) را معرفی کنیم:

L k = T – P،

سپس معادلات (3.20) را می توان به شکل زیر نوشت:

.
(3.21)

معادلات (3.21) معادلات لاگرانژ از نوع دوم برای سیستم های محافظه کار هستند.

بر اساس اصل دالامبر، برابری های زیر معتبر است:

نیروی فعال کجاست - واکنش اتصالات؛ – نیروی اینرسی نقطه (شکل 3.36).

با ضرب اسکالار هر یک از روابط (3.45) در جابجایی احتمالی نقطه و جمع کردن روی تمام نقاط سیستم، به دست می‌آییم.

(3.46)

برابری (3.46) یک معادله کلی از دینامیک برای یک سیستم مکانیکی با هر گونه محدودیت است. اگر اتصالات ایده آل هستند، پس و عبارت (3.46) یکی از اشکال زیر را به خود می گیرد:

معادله عمومی دینامیک (اصل یکپارچه d'Alembert-Lagrange).در هر لحظه از حرکت یک سیستم با اتصالات ایده آل، مجموع کارهای ابتدایی همه نیروهای فعال و نیروهای اینرسی نقاط سیستم در هر حرکت احتمالی سیستم برابر با صفر است.

مختصات تعمیم یافته

اجازه دهید سیستم از ننقاط و موقعیت آن با 3 مشخص می شود نمختصات نقاط سیستم (شکل 3.37). بر نظام تحمیل شده است ل

اتصالات دو طرفه هولونومیک که معادلات آنهاست س=1,2,…,ل.

پس 3 نمختصات مرتبط است لمعادلات و مختصات مستقل خواهد بود n=3ن-ل.

مانند nمختصات مستقل، شما می توانید هر پارامتر مستقل را انتخاب کنید

پارامترهای مستقلی که به طور منحصر به فرد موقعیت سیستم را تعیین می کنند نامیده می شوند مختصات تعمیم یافته سیستم.

برنج. 3.37

به طور کلی، آنها توابعی از مختصات دکارتی نقاط سیستم هستند:

شما می توانید مختصات دکارتی را بر حسب مختصات تعمیم یافته بیان کنید:

برای بردار شعاع هر نقطه از سیستم به دست می آوریم

اگر اتصالات ثابت باشند، زمان به صراحت وارد (3.47) نخواهد شد. برای اتصالات هولونومیک، بردار حرکت احتمالی یک نقطه را می توان به شکل زیر بیان کرد:

اگر اتصالات هولونومیک باشند، تعداد حرکات (یا تغییرات) ممکن مستقل با تعداد مختصات تعمیم یافته مستقل منطبق است. از این رو، تعداد درجات آزادی یک سیستم هولونومیک برابر با تعداد مختصات تعمیم یافته مستقل این سیستم است، یعنی. n=3ن-ل

برای سیستم‌های غیرهولونومیک، در حالت کلی، تعداد تغییرات مستقل (جابجایی‌های احتمالی) کمتر از تعداد مختصات تعمیم‌یافته است. بنابراین، تعداد درجات آزادی یک سیستم غیرهولونومیک، برابر با تعداد جابجایی های ممکن مستقل، از تعداد مختصات تعمیم یافته سیستم نیز کمتر است.

مشتقات مختصات تعمیم یافته نسبت به زمان را سرعت تعمیم یافته می نامند و نشان می دهند

نیروهای تعمیم یافته

برنج. 3.38

تعریف نیروهای تعمیم یافته. یک سیستم هولونومیک از را در نظر بگیرید ننقاط مادی، داشتن nدرجات آزادی و تحت تأثیر سیستمی از نیروها (شکل 3.38). موقعیت سیستم مشخص می شود nمختصات تعمیم یافته آن ها

بردار حرکت ممکن -

(3.48)

اجازه دهید مجموع کارهای اولیه نیروهای وارد بر سیستم را بر روی جابجایی احتمالی سیستم محاسبه کنیم:

(3.49)

با جایگزینی (3.48) به (3.49) و تغییر ترتیب جمع، به دست می آوریم

(3.50)

کمیت اسکالر نیروی تعمیم یافته مربوط به مختصات تعمیم یافته q i نامیده می شود.

ابعاد نیروی تعمیم یافته. از فرمول (3.50) بعد نیروی تعمیم یافته [ س]=[آ]/[q]. اگر مختصات تعمیم یافته دارای بعد طول باشد، نیروی تعمیم یافته دارای بعد نیرو [N] است، اما اگر مختصات تعمیم یافته یک زاویه باشد (بعد – 1)، نیروی تعمیم یافته دارای بعد گشتاور نیرو [N] است. N×m].

محاسبه نیروهای تعمیم یافته. 1. نیروی تعمیم یافته را می توان با استفاده از فرمولی که آن را تعیین می کند محاسبه کرد:

جایی که F kx,فیکس,F kz- پیش بینی نیرو بر روی محورهای مختصات؛ x k,y yx,z k- مختصات نقطه اعمال نیرو

2. نیروهای تعمیم یافته ضرایبی برای تغییرات متناظر مختصات تعمیم یافته در بیان کار ابتدایی هستند (3.50):

3. اگر به سیستم یک حرکت احتمالی گفته شود که فقط یک مختصات تعمیم یافته تغییر کند q jسپس از (3.52) داریم

فهرست مطالب چیدر عدد نشان می دهد که مجموع کار بر روی یک حرکت ممکن محاسبه می شود که در طی آن فقط مختصات تغییر می کند (متغیر است) چی.

4. برای نیروهای بالقوه:

(3.53)

تابع نیرو کجاست

از عبارت (3.51) با در نظر گرفتن برابری های (3.53) نتیجه می شود که

بدین ترتیب،

انرژی پتانسیل سیستم کجاست

3.5.6. معادله کلی دینامیک در نیروهای تعمیم یافته.
شرایط تعادل قوا

معادله دینامیک عمومی (3.50)

بردار حرکت ممکن مطابق (3.48) برابر است با

با در نظر گرفتن این عبارت، معادله کلی دینامیک شکل می گیرد

بیایید آن را با تغییر ترتیب جمع تبدیل کنیم

(3.54)

اینجا - نیروی تعمیم یافته نیروهای فعال مطابق با مختصات تعمیم یافته چی; - نیروی اینرسی تعمیم یافته مربوط به مختصات تعمیم یافته چیسپس معادله (3.54) شکل می گیرد

افزایش مختصات تعمیم یافته دلخواه و مستقل از یکدیگر است. بنابراین، ضرایب آنها در آخرین معادله باید برابر با صفر باشد:

(3.55)

این معادلات معادل معادله عمومی دینامیک هستند.

اگر نیروهای وارد بر یک سیستم مکانیکی معادل صفر باشد، یعنی. اگر یک سیستم مکانیکی به طور یکنواخت در یک خط مستقیم حرکت کند یا حالت سکون را حفظ کند، نیروهای اینرسی نقاط آن برابر با صفر است. در نتیجه، نیروهای اینرسی تعمیم یافته سیستم برابر با صفر است ، سپس معادلات (3.55) شکل می گیرند

(3.56)

تساوی (3.56) شرایط تعادل نیروها را در نیروهای تعمیم یافته بیان می کند.

در مورد نیروهای محافظه کار

در نتیجه، شرایط تعادل یک سیستم محافظه کار نیروها شکل می گیرد

معادله کلی دینامیک برای یک سیستم با هر گونه اتصال (اصل ترکیبی D'Alembert-Lagrangeیا معادله کلی مکانیک):

نیروی فعال وارد شده به نقطه سیستم کجاست. - قدرت واکنش پیوندها؛ - نیروی اینرسی نقطه ای؛ - حرکت احتمالی

در حالت تعادل سیستم، وقتی تمام نیروهای اینرسی نقاط سیستم از بین برود، به اصل جابجایی های احتمالی تبدیل می شود. معمولاً برای سیستم‌هایی با اتصالات ایده‌آل استفاده می‌شود که شرایط برای آنها برآورده می‌شود

در این مورد (229) یکی از اشکال زیر را به خود می گیرد:

,

,

. (230)

بدین ترتیب، بر اساس معادله کلی دینامیک، در هر لحظه از حرکت یک سیستم با اتصالات ایده آل، مجموع کارهای اولیه همه نیروهای فعال و نیروهای اینرسی نقاط سیستم برابر با صفر در هر حرکت احتمالی سیستم مجاز است. توسط اتصالات.

معادله کلی دینامیک را می توان اشکال معادل دیگری نیز ارائه داد. با گسترش حاصل ضرب اسکالر بردارها، می توان آن را به صورت بیان کرد

مختصات نقطه ام سیستم کجاست. با توجه به اینکه پیش بینی نیروهای اینرسی بر روی محورهای مختصات از طریق پیش بینی شتاب ها بر روی این محورها توسط روابط بیان می شود.

,

معادله کلی دینامیک را می توان شکل داد

در این شکل نامیده می شود معادله کلی دینامیک به صورت تحلیلی.

هنگام استفاده از معادله کلی دینامیک، لازم است بتوانیم کار اولیه نیروهای اینرسی سیستم را بر روی جابجایی های احتمالی محاسبه کنیم. برای انجام این کار، فرمول های مربوطه را برای کار ابتدایی به دست آمده برای نیروهای معمولی اعمال کنید. اجازه دهید کاربرد آنها را برای نیروهای اینرسی یک جسم صلب در موارد خاصی از حرکت آن در نظر بگیریم.

در حین حرکت رو به جلو در این حالت بدن دارای سه درجه آزادی است و به دلیل محدودیت های تحمیلی فقط می تواند حرکت انتقالی را انجام دهد. حرکات احتمالی بدن که امکان اتصال را فراهم می کند نیز انتقالی هستند.

نیروهای اینرسی در طول حرکت انتقالی به نتیجه کاهش می یابد . برای مجموع کارهای اولیه نیروهای اینرسی در حرکت انتقالی ممکن یک جسم، به دست می آوریم

جابجایی احتمالی مرکز جرم و هر نقطه از بدن کجاست، زیرا جابجایی ممکن انتقالی همه نقاط بدن یکسان است: شتاب ها نیز یکسان هستند، یعنی.

هنگامی که یک جسم صلب حول یک محور ثابت می چرخد. بدن در این حالت یک درجه آزادی دارد. می تواند حول یک محور ثابت بچرخد. حرکت احتمالی که توسط اتصالات روی هم قرار داده شده است نیز چرخش بدنه توسط یک زاویه ابتدایی حول یک محور ثابت است.

نیروهای اینرسی کاهش یافته به نقطه ای از محور چرخش به بردار اصلی و ممان اصلی کاهش می یابد. بردار اصلی نیروهای اینرسی به یک نقطه ثابت اعمال می شود و کار اولیه آن روی جابجایی احتمالی صفر است. برای لحظه اصلی نیروهای اینرسی، کار ابتدایی غیرصفر تنها با پیش بینی آن بر روی محور چرخش انجام می شود. بنابراین، برای مجموع کار نیروهای اینرسی بر روی جابجایی احتمالی در نظر گرفته شده است

,

اگر زاویه در جهت فلش کمانی شتاب زاویه ای گزارش شود.

در حرکت صاف. در این حالت، محدودیت های اعمال شده بر بدنه صلب فقط امکان حرکت مسطح ممکن را فراهم می کند. در حالت کلی، شامل یک حرکت انتقالی ممکن همراه با یک قطب است که مرکز جرم را برای آن انتخاب می کنیم، و یک چرخش در یک زاویه ابتدایی حول محوری که از مرکز جرم و عمود بر صفحه موازی آن می گذرد. بدن می تواند حرکت هواپیما را انجام دهد.

معرفی

سینماتیک به شرح ساده ترین انواع حرکات مکانیکی می پردازد. در این مورد، دلایل ایجاد تغییر در موقعیت بدن نسبت به سایر اجسام مورد بررسی قرار نگرفت و سیستم مرجع به دلایل راحتی هنگام حل یک مشکل خاص انتخاب شد. در دینامیک، اول از همه، دلایل شروع حرکت برخی اجسام نسبت به اجسام دیگر و همچنین عوامل ایجاد کننده شتاب، مورد توجه است. با این حال، قوانین در مکانیک، به طور دقیق، در سیستم های مرجع مختلف اشکال متفاوتی دارند. مشخص شده است که چنین سیستم های مرجعی وجود دارند که در آنها قوانین و الگوها به انتخاب سیستم مرجع بستگی ندارد. چنین سیستم های مرجع نامیده می شوند سیستم های اینرسی(ISO). در این سیستم های مرجع، بزرگی شتاب فقط به نیروهای عامل بستگی دارد و به انتخاب سیستم مرجع بستگی ندارد. چارچوب اینرسی مرجع است چارچوب مرجع هلیوسنتریککه مبدأ آن در مرکز خورشید است. سیستم های مرجع که به طور یکنواخت به صورت مستقیم نسبت به سیستم اینرسی حرکت می کنند نیز اینرسی هستند و سیستم های مرجع که با شتاب نسبت به سیستم اینرسی حرکت می کنند. غیر اینرسی. به این دلایل، سطح زمین، به طور دقیق، یک چارچوب مرجع غیر اینرسی است. در بسیاری از مسائل، چارچوب مرجع مرتبط با زمین را می توان با درجه دقت خوبی، اینرسی در نظر گرفت.

قوانین اساسی دینامیک در اینرسی و غیر اینرسی

سیستم های مرجع

توانایی جسم برای حفظ حالت حرکت مستقیم یکنواخت یا در حالت سکون در ISO نامیده می شود. اینرسی بدن. اندازه گیری اینرسی بدن است وزن. جرم یک کمیت اسکالر است که در سیستم SI بر حسب کیلوگرم (کیلوگرم) اندازه گیری می شود. معیار کنش متقابل کمیتی است به نام به زور. نیرو یک کمیت برداری است که بر حسب نیوتن (N) در سیستم SI اندازه گیری می شود.

قانون اول نیوتن در سیستم های مرجع اینرسی، نقطه ای به طور یکنواخت در یک خط مستقیم حرکت می کند یا در حالت سکون است اگر مجموع تمام نیروهای وارد بر آن برابر با صفر باشد، یعنی:

نیروهای وارد بر یک نقطه مشخص کجا هستند.

قانون دوم نیوتن در سیستم های اینرسی، جسمی با شتاب حرکت می کند که مجموع نیروهای وارد بر آن برابر با صفر نباشد و حاصل ضرب جرم جسم و شتاب آن برابر با مجموع این نیروها باشد، یعنی:

قانون سوم نیوتن نیروهایی که اجسام بر یکدیگر اثر می کنند از نظر قدر مساوی و در جهت مخالف هستند، یعنی: .

نیروها به عنوان معیارهای کنش متقابل، همیشه به صورت جفت متولد می شوند.

برای حل موفقیت آمیز اکثر مسائل با استفاده از قوانین نیوتن، لازم است به دنباله خاصی از اقدامات (نوعی الگوریتم) پایبند باشیم.

نکات اصلی الگوریتم

1. وضعیت مشکل را تجزیه و تحلیل کنید و دریابید که بدن مورد نظر با کدام اجسام تعامل دارد. بر این اساس مقدار نیروهای وارد بر جسم مورد نظر را مشخص کنید. فرض کنید تعداد نیروهای وارد بر جسم برابر است. سپس یک نقشه شماتیک درست کنید که تمام نیروهای وارد بر بدن را روی آن رسم کنید.

2. با استفاده از شرط مسئله جهت شتاب جسم مورد نظر را تعیین کنید و بردار شتاب را در شکل به تصویر بکشید.

3. قانون دوم نیوتن را به صورت برداری بنویسید، یعنی:

جایی که نیروهای وارد بر بدن

4. یک سیستم مرجع اینرسی را انتخاب کنید. در شکل یک سیستم مختصات دکارتی مستطیلی را رسم کنید که محور OX آن در امتداد بردار شتاب هدایت شده است، محور OY و OZ عمود بر محور OX هدایت می شوند.

5. با استفاده از ویژگی اصلی برابری های برداری، قانون دوم نیوتن را برای پیش بینی بردارها بر روی محورهای مختصات بنویسید، به عنوان مثال:

6. اگر در مسئله ای علاوه بر نیروها و شتاب ها، مختصات و سرعت نیز لازم باشد، علاوه بر قانون دوم نیوتن، از معادلات حرکتی حرکت نیز لازم است. با نوشتن یک سیستم معادلات، باید به این نکته توجه کرد که تعداد معادلات با تعداد مجهولات این مسئله برابر است.

اجازه دهید یک قاب مرجع غیر اینرسی را در نظر بگیریم که با سرعت زاویه ای ثابت حول محوری که به صورت انتقالی با سرعتی نسبت به قاب اینرسی حرکت می کند، می چرخد. در این حالت، شتاب یک نقطه در قاب اینرسی () با شتاب در قاب غیر اینرسی () با رابطه:

که در آن شتاب سیستم غیر اینرسی نسبت به سیستم اینرسی، سرعت خطی یک نقطه در سیستم غیر اینرسی است. از آخرین رابطه، به جای شتاب، برابری (1) را جایگزین می کنیم، عبارت را به دست می آوریم:

این نسبت نامیده می شود قانون دوم نیوتن در چارچوب مرجع غیر اینرسی.

نیروهای اینرسی اجازه دهید نماد زیر را معرفی کنیم:

1. – نیروی اینرسی رو به جلو;

2. – نیروی کوریولیس;

3 – نیروی گریز از مرکز اینرسی.

در مسائل، نیروی انتقالی اینرسی در برابر بردار با شتاب حرکت انتقالی یک قاب مرجع غیر اینرسی نشان داده می شود ()، نیروی گریز از مرکز اینرسی از مرکز چرخش در امتداد شعاع نشان داده می شود (). جهت نیروی کوریولیس توسط قانون تعیین می شود گیملتبرای حاصل ضرب بردارها.

به بیان دقیق، نیروهای اینرسی به معنای کامل نیرو نیستند، زیرا قانون سوم نیوتن برای آنها صدق نمی کند، یعنی. آنها جفت نیستند.

قدرت ها

نیروی گرانش جهانی. نیروی گرانش جهانی در فرآیند برهمکنش بین اجسام با جرم ها بوجود می آید و از رابطه زیر محاسبه می شود:

. (4)

ضریب تناسب نامیده می شود ثابت گرانشی. مقدار آن در سیستم SI برابر است با .

قدرت واکنش. نیروهای واکنش زمانی به وجود می آیند که یک جسم با ساختارهای مختلفی که موقعیت آن را در فضا محدود می کند برهمکنش می کند. به عنوان مثال، جسمی که بر روی یک نخ معلق است، توسط یک نیروی واکنشی که معمولاً نیرو نامیده می شود، وارد عمل می شود. تنش نیروی کشش نخ همیشه در امتداد نخ هدایت می شود.هیچ فرمولی برای محاسبه مقدار آن وجود ندارد. معمولاً مقدار آن از قانون اول یا دوم نیوتن بدست می آید. نیروهای واکنش نیز شامل نیروهایی است که بر روی یک ذره روی سطح صاف اثر می‌گذارند. به او زنگ می زنند نیروی واکنش طبیعی، مشخص کن . نیروی واکنش همیشه عمود بر سطح مورد نظر هدایت می شود. نیرویی که بر روی سطح صاف از سمت بدن وارد می شود نامیده می شود نیروی فشار عادی(). بر اساس قانون سوم نیوتن، نیروی واکنش برابر با نیروی فشار عادی است، اما بردارهای این نیروها در جهت مخالف هستند.

نیروی الاستیک. در صورت تغییر شکل اجسام، نیروهای کشسان در اجسام ایجاد می شود. اگر شکل بدن یا حجم آن تغییر کند. هنگامی که تغییر شکل متوقف می شود، نیروهای الاستیک ناپدید می شوند. لازم به ذکر است که اگرچه نیروهای الاستیک در هنگام تغییر شکل اجسام به وجود می آیند، تغییر شکل همیشه منجر به ظهور نیروهای کشسان نمی شود. نیروهای ارتجاعی در اجسامی که قادر به بازیابی شکل خود پس از توقف تأثیر خارجی هستند، بوجود می آیند. چنین اجسام و تغییر شکل های مربوطه نامیده می شوند کشسان. با تغییر شکل پلاستیک، تغییرات پس از قطع نفوذ خارجی به طور کامل ناپدید نمی شوند. یک مثال بارز از تجلی نیروهای الاستیک می تواند نیروهای ناشی از فنرهای در معرض تغییر شکل باشد. برای تغییر شکل‌های الاستیکی که در اجسام تغییر شکل‌یافته رخ می‌دهند، نیروی الاستیک همیشه متناسب با بزرگی تغییر شکل است، یعنی:

, (5)

ضریب کشش (یا سفتی) فنر، بردار تغییر شکل فنر کجاست.

این بیانیه نامیده می شود قانون هوک

نیروی اصطکاک. هنگامی که یک جسم در امتداد سطح جسم دیگر حرکت می کند، نیروهایی به وجود می آیند که مانع از این حرکت می شوند. چنین نیروهایی معمولاً نامیده می شوند نیروهای اصطکاک لغزشی. مقدار نیروی اصطکاک ایستا بسته به نیروی خارجی اعمال شده می تواند متفاوت باشد. در مقدار معینی از نیروی خارجی، نیروی اصطکاک ساکن به حداکثر مقدار خود می رسد. پس از این، بدن شروع به سر خوردن می کند. به طور تجربی ثابت شده است که نیروی اصطکاک لغزشی به طور مستقیم با نیروی فشار عادی بدن بر روی سطح متناسب است.طبق قانون سوم نیوتن، نیروی فشار عادی یک جسم بر روی یک سطح، همیشه برابر با نیروی واکنشی است که خود سطح روی جسم متحرک وارد می کند. با در نظر گرفتن این موضوع، فرمول محاسبه مقدار نیروی اصطکاک لغزشی به شکل زیر است:

, (6)

بزرگی نیروی واکنش کجاست. ضریب اصطکاک لغزشی نیروی اصطکاک لغزشی که بر روی یک جسم متحرک وارد می‌شود، همیشه بر خلاف سرعت آن، در امتداد سطوح در تماس است.

قدرت مقاومت. هنگامی که اجسام در مایعات و گازها حرکت می کنند، نیروهای اصطکاک نیز ایجاد می شوند، اما تفاوت قابل توجهی با نیروهای اصطکاک خشک دارند. این نیروها نامیده می شوند نیروهای اصطکاک چسبناک، یا نیروهای مقاومت. نیروهای اصطکاک چسبناک فقط در حین حرکت نسبی اجسام بوجود می آیند. نیروهای مقاومت به عوامل زیادی بستگی دارد، از جمله: به اندازه و شکل اجسام، به خواص محیط (چگالی، ویسکوزیته)، به سرعت حرکت نسبی. در سرعت های پایین، نیروی پسا نسبت مستقیمی با سرعت بدنه نسبت به محیط دارد، یعنی:

. (7)

در سرعت های بالا، نیروی پسا متناسب با مجذور سرعت بدنه نسبت به محیط است، یعنی:

, (8)

که در آن برخی از ضرایب تناسب نامیده می شوند ضرایب مقاومت.

معادله پایه دینامیک

معادله اساسی دینامیک یک نقطه مادی چیزی نیست جز بیان ریاضی قانون دوم نیوتن:

. (9)

در چارچوب مرجع اینرسی، مجموع همه نیروها فقط شامل نیروهایی می شود که معیارهای اندرکنش هستند؛ در چارچوب های غیر اینرسی، مجموع نیروها شامل نیروهای اینرسی است.

از دیدگاه ریاضی، رابطه (9) معادله دیفرانسیل حرکت یک نقطه به صورت برداری است. راه حل آن مشکل اصلی دینامیک یک نقطه مادی است.

نمونه هایی از حل مسئله

وظیفه شماره 1. یک لیوان روی یک ورق کاغذ قرار می گیرد. اگر ضریب اصطکاک شیشه و ورق کاغذ 0.3 باشد ورق را با چه شتابی باید به حرکت در آورد تا از زیر شیشه بیرون بیاید؟

فرض کنید با مقداری نیرویی که بر روی یک ورق کاغذ وارد می شود، شیشه با ورق حرکت می کند. اجازه دهید به طور جداگانه نیروهای وارد بر یک شیشه با جرم را به تصویر بکشیم. اجسام زیر روی شیشه عمل می کنند: زمین با نیروی گرانش، ورق کاغذ با نیروی واکنش، ورق کاغذ با نیروی اصطکاک که در امتداد سرعت حرکت شیشه هدایت می شود. حرکت شیشه به طور یکنواخت شتاب می گیرد، بنابراین بردار شتاب در امتداد سرعت حرکت شیشه هدایت می شود.

اجازه دهید بردار شتاب شیشه را در شکل به تصویر بکشیم. بیایید قانون دوم نیوتن را به صورت برداری برای نیروهای وارد بر شیشه بنویسیم:

.

اجازه دهید محور OX را در امتداد بردار شتاب شیشه، و محور OY را به صورت عمودی به سمت بالا هدایت کنیم. بیایید قانون دوم نیوتن را بر روی این محورهای مختصات بنویسیم و معادلات زیر را بدست آوریم:

(1.1)

با افزایش نیروی وارد بر ورق کاغذ، مقدار نیروی اصطکاکی که ورق کاغذ بر روی شیشه وارد می کند افزایش می یابد. در مقدار معینی از نیرو، بزرگی نیروی اصطکاک به حداکثر مقدار خود می رسد که از نظر بزرگی برابر با نیروی اصطکاک لغزشی است. از این لحظه لیوان نسبت به سطح کاغذ شروع به لیز خوردن می کند. مقدار محدود کننده نیروی اصطکاک مربوط به نیروی واکنشی است که بر روی شیشه اعمال می شود به شرح زیر:

از برابری (1.2) مقدار نیروی واکنش را بیان می کنیم و سپس آن را با آخرین رابطه جایگزین می کنیم. از رابطه حاصل، مقدار نیروی اصطکاک را پیدا کرده و آن را در برابر (1.1) قرار می دهیم، عبارتی برای تعیین حداکثر شتاب شیشه به دست می آوریم:

با جایگزینی مقادیر عددی کمیت ها به آخرین برابری، مقدار حداکثر شتاب شیشه را پیدا می کنیم:

.

مقدار شتاب حاصل از شیشه برابر است با حداقل شتاب یک ورق کاغذ که می توان آن را از زیر شیشه "بیرون کشید".

پاسخ: .

بیایید تمام نیروهای وارد بر بدن را به تصویر بکشیم. علاوه بر نیروی خارجی، زمین با نیروی گرانش، سطح افقی با نیروی واکنش و نیروی اصطکاک که بر خلاف سرعت جسم است، به بدن وارد می شود. بدن با شتاب یکنواخت حرکت می کند و بنابراین، بردار شتاب آن در امتداد سرعت حرکت هدایت می شود. بیایید بردار را در شکل به تصویر بکشیم. همانطور که در شکل نشان داده شده است سیستم مختصات را انتخاب می کنیم. قانون دوم نیوتن را به صورت برداری می نویسیم:

.

با استفاده از ویژگی اصلی برابری های برداری، معادلات پیش بینی بردارهای موجود در آخرین برابری بردار را می نویسیم:

رابطه نیروی اصطکاک لغزشی را یادداشت می کنیم

از برابری (2.2) مقدار نیروی واکنش را می یابیم

از عبارت به دست آمده، به جای مقدار نیروی واکنش، برابری (2.3) را جایگزین می کنیم، عبارت را به دست می آوریم.

با جایگزینی عبارت حاصل از نیروی اصطکاک به برابری (2.1)، فرمولی برای محاسبه شتاب جسم خواهیم داشت:

داده های عددی در سیستم SI را با آخرین فرمول جایگزین می کنیم و مقدار شتاب بار را پیدا می کنیم:

پاسخ: .

برای کمترین مقدار نیرو، جهت نیروی اصطکاک را که بر روی بلوک ساکن عمل می کند، تعیین می کنیم. بیایید تصور کنیم که نیرو کمتر از حداقل نیروی کافی برای ماندن بدن در حالت سکون است. در این حالت بدن به سمت پایین حرکت می کند و نیروی اصطکاک وارد شده به آن به صورت عمودی به سمت بالا هدایت می شود. برای اینکه بدن را متوقف کنید، باید مقدار نیروی اعمال شده را افزایش دهید. علاوه بر این، این جسم توسط زمین با نیروی گرانشی که به صورت عمودی به سمت پایین هدایت می شود و همچنین توسط دیواری با نیروی واکنشی که به صورت افقی به سمت چپ هدایت می شود، وارد عمل می شود. اجازه دهید تمام نیروهای وارد بر بدن را در شکل به تصویر بکشیم. بیایید یک سیستم مختصات دکارتی مستطیلی را در نظر بگیریم که محورهای آن مطابق شکل نشان داده شده است. برای جسمی که در حال سکون است، قانون اول نیوتن را به صورت برداری می نویسیم:

.

برای برابری بردار پیدا شده، تساوی های پیش بینی بردارها را روی محورهای مختصات می نویسیم، معادلات زیر را به دست می آوریم:

در حداقل مقدار نیروی خارجی، مقدار نیروی اصطکاک ساکن به حداکثر مقدار برابر با مقدار نیروی اصطکاک لغزشی می رسد:

از برابری (3.1) مقدار نیروی واکنش را پیدا کرده و آن را با برابری (3.3) جایگزین می کنیم، عبارت زیر را برای نیروی اصطکاک به دست می آوریم:

.

اجازه دهید سمت راست این رابطه را به جای نیروی اصطکاک در برابری (3.2) جایگزین کنیم و فرمولی برای محاسبه مقدار نیروی اعمال شده بدست آوریم:

از آخرین فرمول، مقدار نیرو را می یابیم:

.

پاسخ: .

بیایید تمام نیروهایی را که بر روی توپی که به صورت عمودی به سمت پایین در هوا حرکت می کند را به تصویر بکشیم. زمین با نیروی گرانش و هوا با نیروی مقاومت بر آن اثر می گذارد. اجازه دهید نیروهای در نظر گرفته شده در شکل را به تصویر بکشیم. در لحظه اولیه زمان، برآیند تمام نیروها دارای حداکثر مقدار است، زیرا سرعت توپ صفر و نیروی مقاومت نیز صفر است. در این لحظه توپ حداکثر شتابی برابر با . با حرکت توپ، سرعت آن افزایش می یابد و در نتیجه نیروی مقاومت هوا افزایش می یابد. در نقطه ای از زمان، نیروی مقاومت به مقداری برابر با نیروی گرانش می رسد. از این زمان توپ به طور یکنواخت حرکت می کند. بیایید اولین قانون نیوتن را به صورت برداری برای حرکت یکنواخت یک توپ بنویسیم:

.

بیایید محور OY را به صورت عمودی به سمت پایین هدایت کنیم. برای این برابری برداری، اجازه دهید برابری پیش بینی بردارها را روی محور OY بنویسیم:

. (4.1)

نیروی مقاومت به سطح مقطع توپ و مقدار سرعت آن به شرح زیر بستگی دارد:

, (4.2)

کجا ضریب تناسب است که ضریب مقاومت نامیده می شود.

از برابری های (4.1) و (4.2) رابطه زیر به دست می آید:

. (4.3)

اجازه دهید جرم توپ را از طریق چگالی و حجم آن و حجم آن را به نوبه خود از طریق شعاع توپ بیان کنیم:

. (4.4)

از این عبارت جرم را پیدا کرده و با برابری (4.3) جایگزین می کنیم، برابری زیر را به دست می آوریم:

. (4.5)

سطح مقطع توپ را بر حسب شعاع آن بیان می کنیم:

با در نظر گرفتن رابطه (4.6)، برابری (4.5) به شکل زیر خواهد بود:

.

اجازه دهید شعاع اولین توپ را نشان دهیم. به عنوان شعاع توپ دوم. اجازه دهید فرمول سرعت حرکت ثابت توپ اول و دوم را بنویسیم:

از برابری های به دست آمده نسبت سرعت را پیدا می کنیم:

.

از شرایط مسئله، نسبت شعاع توپ ها برابر با دو است. با استفاده از این شرط، نسبت سرعت را پیدا می کنیم:

.

پاسخ: .

جسمی که در امتداد صفحه شیبدار به سمت بالا حرکت می کند توسط اجرام خارجی تحت تأثیر قرار می گیرد: الف) زمین با گرانش به صورت عمودی به سمت پایین. ب) صفحه مایل با نیروی واکنش عمود بر صفحه شیبدار. ج) صفحه شیب دار با نیروی اصطکاک که بر خلاف حرکت بدن است. د) جسم خارجی با نیرویی که در امتداد صفحه شیبدار به سمت بالا هدایت می شود. تحت تأثیر این نیروها، جسم با شتاب یکنواخت به سمت صفحه شیبدار حرکت می کند و بنابراین، بردار شتاب در امتداد حرکت جسم هدایت می شود. بیایید بردار شتاب را در شکل به تصویر بکشیم. بیایید قانون دوم نیوتن را به صورت برداری بنویسیم:

.

اجازه دهید یک سیستم مختصات دکارتی مستطیلی را انتخاب کنیم که محور OX آن در امتداد شتاب بدنه و محور OY عمود بر صفحه شیبدار است. بیایید قانون دوم نیوتن را بر روی این محورهای مختصات بنویسیم و معادلات زیر را بدست آوریم:

نیروی اصطکاک لغزشی با نیروی واکنش با رابطه زیر مرتبط است:

از برابری (5.2) مقدار نیروی واکنش را پیدا کرده و آن را با برابری (5.3) جایگزین می کنیم، عبارت زیر را برای نیروی اصطکاک داریم:

. (5.4)

با جایگزینی سمت راست برابری (5.4) به برابری (5.1) به جای نیروی اصطکاک، معادله زیر را برای محاسبه مقدار نیروی مورد نیاز بدست می آوریم:

بیایید بزرگی نیرو را محاسبه کنیم:

پاسخ: .

بیایید تمام نیروهایی را که بر روی بدنه ها و روی بلوک اعمال می کنند به تصویر بکشیم. اجازه دهید روند حرکت اجسامی را که با نخی که روی یک بلوک پرتاب می شود به هم متصل شده اند در نظر بگیریم. نخ بی وزن و غیر قابل امتداد است، بنابراین، مقدار نیروی کشش در هر بخش از نخ یکسان خواهد بود، یعنی. و .

جابجایی اجسام در هر دوره زمانی یکسان خواهد بود و بنابراین در هر لحظه از زمان مقادیر سرعت و شتاب این اجسام یکسان خواهد بود. از این که بلوک بدون اصطکاک می چرخد ​​و وزن ندارد، نتیجه می شود که نیروی کشش نخ در دو طرف بلوک یکسان خواهد بود، یعنی: .

این نشان دهنده برابری نیروهای کششی نخ است که بر روی بدنه اول و دوم عمل می کنند، یعنی. . اجازه دهید بردارهای شتاب جسم اول و دوم را در شکل نشان دهیم. اجازه دهید دو تبر OX را به تصویر بکشیم. بیایید محور اول را در امتداد بردار شتاب جسم اول هدایت کنیم، دوم - در امتداد بردار شتاب بدن دوم. بیایید قانون دوم نیوتن را برای هر جسمی که بر روی این محورهای مختصات پیش بینی می شود، بنویسیم:

با توجه به اینکه و با بیان از معادله اول، در معادله دوم جایگزین می کنیم، به دست می آید

از آخرین برابری مقدار شتاب را پیدا می کنیم:

.

از برابری (1) مقدار نیروی کشش را می یابیم:

پاسخ: , .

همانطور که حلقه کوچک به دور محیط خود می چرخد، دو نیرو بر آن وارد می شود: نیروی گرانش که به صورت عمودی به سمت پایین هدایت می شود و نیروی واکنشی که به سمت مرکز حلقه هدایت می شود. بیایید این نیروها را در شکل به تصویر بکشیم و همچنین مسیر حلقه را روی آن نشان دهیم. بردار شتاب مرکز محور حلقه در صفحه مسیر قرار دارد و به سمت محور چرخش هدایت می شود. بیایید آن را در تصویر به تصویر بکشیم. بیایید قانون دوم نیوتن را به صورت برداری برای یک حلقه در حال چرخش بنویسیم:

.

بیایید یک سیستم مختصات مستطیلی را انتخاب کنیم، که محور OX آن در امتداد شتاب مرکز، و محور OY - به صورت عمودی به سمت بالا در امتداد محور چرخش هدایت می شود. بیایید قانون دوم نیوتن را در پیش بینی ها روی این محورهای مختصات بنویسیم:

از برابری (7.2) مقدار نیروی واکنش را پیدا کرده و آن را با برابری (7.1) جایگزین می کنیم، عبارت را به دست می آوریم:

. (7.3)

شتاب مرکزگرا به صورت زیر به سرعت دورانی مربوط می شود: ، شعاع چرخش حلقه کوچک کجاست. با جایگزینی سمت راست آخرین برابری به جای فرمول (7.3)، رابطه زیر را بدست می آوریم:

. (7.4)

از شکل، مقدار مماس زاویه آلفا را می یابیم . با در نظر گرفتن این عبارت، برابری (7.4) به شکل زیر خواهد بود:

از آخرین معادله ارتفاع مورد نیاز را پیدا می کنیم:

پاسخ: .

بر جسمی که با دیسک می چرخد، سه نیرو وارد می شود: گرانش، نیروی واکنش و نیروی اصطکاک که به سمت محور چرخش هدایت می شود. بیایید تمام نیروها را در شکل به تصویر بکشیم. اجازه دهید در این شکل جهت بردار شتاب مرکزگرا را نشان دهیم. قانون دوم نیوتن را به صورت برداری می نویسیم:

.

اجازه دهید یک سیستم مختصات دکارتی مستطیلی را همانطور که در شکل نشان داده شده است انتخاب کنیم. بیایید قانون دوم نیوتن را در پیش بینی ها روی محورهای مختصات بنویسیم:

; (8.1)

. (8.2)

بیایید رابطه شتاب مرکزگرا را بنویسیم:

. (8.3)

اجازه دهید سمت راست برابری (8.3) را به جای شتاب مرکزگرا با برابری (8.1) جایگزین کنیم، به دست می آوریم:

. (8.4)

از برابری (8.4) مشخص می شود که بزرگی نیروی اصطکاک با شعاع چرخش رابطه مستقیم دارد، بنابراین، با افزایش شعاع چرخش، نیروی اصطکاک ساکن افزایش می یابد و در مقدار معینی نیروی اصطکاک ایستا به یک عدد می رسد. حداکثر مقدار برابر با نیروی اصطکاک لغزشی ().

با در نظر گرفتن برابری (8.2)، عباراتی را برای حداکثر نیروی اصطکاک استاتیک به دست می آوریم:

.

با جایگزینی سمت راست برابری حاصل به جای نیروی اصطکاک با برابری (4)، رابطه زیر را بدست می آوریم:

از این معادله مقدار محدود شعاع چرخش را می یابیم:

پاسخ: .

در طول پرواز یک قطره، دو نیرو بر روی آن وارد می شود: جاذبه و نیروی کشش. بیایید تمام نیروها را در شکل به تصویر بکشیم. اجازه دهید یک محور عمودی OY را انتخاب کنیم که مبدأ آن در سطح زمین قرار دارد. بیایید معادله اصلی دینامیک را بنویسیم:

.

با طرح برابری بر روی محور OY، رابطه زیر را خواهیم داشت:

بیایید هر دو طرف آخرین تساوی را بر تقسیم کنیم و همزمان هر دو ضلع را در ضرب کنیم، با در نظر گرفتن اینکه، عبارت را به دست می آوریم:

بیایید هر دو طرف این عبارت را بر تقسیم کنیم ، رابطه را دریافت می کنیم:

.

رابطه دوم را ادغام می کنیم و وابستگی سرعت به زمان را بدست می آوریم: .

ثابت را از شرایط اولیه پیدا می کنیم ( ، وابستگی مطلوب سرعت را به زمان بدست می آوریم:

.

حداکثر سرعت را از روی شرط تعیین می کنیم :

.

پاسخ: ; .

اجازه دهید در شکل نیروهایی را که بر جنک وارد می‌شوند به تصویر بکشیم. بیایید قانون دوم نیوتن را در پیش بینی ها روی محورهای OX، OY و OZ بنویسیم

زیرا , سپس برای کل مسیر حرکت واشر، فرمول برای نیروی اصطکاک معتبر است، که با در نظر گرفتن برابری OZ، به شکل زیر تبدیل می شود:

با در نظر گرفتن این رابطه، برابری برای محور OX شکل خواهد گرفت

قانون دوم نیوتن را روی مماس مسیر پیک در نقطه مورد بررسی قرار می دهیم و این رابطه را به دست می آوریم:

بزرگی شتاب مماسی کجاست. با مقایسه سمت راست تساوی های آخر نتیجه می گیریم که .

از آنجایی که و، پس با در نظر گرفتن رابطه قبلی، برابری داریم که ادغام آن منجر به عبارت، جایی که ثابت ادغام است. بیایید در آخرین عبارت جایگزین کنیم ، وابستگی سرعت به زاویه را بدست می آوریم:

اجازه دهید ثابت را از شرایط اولیه تعیین کنیم (زمانی که . ) . با در نظر گرفتن این موضوع، وابستگی نهایی را یادداشت می کنیم

.

حداقل مقدار سرعت زمانی به دست می آید که بردار سرعت به موازات محور OX هدایت شود و مقدار آن برابر باشد.

مثالی از حل مسئله با استفاده از معادله کلی دینامیک (اصل دالامبر-لاگرانژ) برای سیستمی با بدنه‌های صلب، وزنه‌ها، قرقره‌ها و بلوک‌هایی که توسط رزوه‌هایی به هم متصل شده‌اند.

محتوا

وظیفه

سیستم مکانیکی شامل قرقره های پلکانی یکنواخت 1 و 2 پیچیده شده در نخ ها، وزنه های 3-6 متصل به این نخ ها و یک بلوک بدون وزن است. این سیستم در یک صفحه عمودی تحت تأثیر گرانش و یک جفت نیرو با یک ممان M = حرکت می کند 10 نیوتن متر، به قرقره 1 اعمال می شود. شعاع پله های قرقره 1 برابر است با: R 1 = 0.2 متر، r 1 = 0.1 متر، و قرقره 2 - R 2 = 0.3 متر، r 2 = 0.15 متر; شعاع چرخش آنها نسبت به محورهای چرخش به ترتیب برابر ρ است 1 = 0.1 مترو ρ 2 = 0.2 متر.

با غفلت از اصطکاک، شتاب بار را تعیین کنید 5. وزن قرقره ها و بارها آورده شده است: P 1 = 40 نیوتن، پ 2 = 0 ، پ 3 = 0 ، پ 4 = 20 نیوتن، پ 5 = 30 نیوتن، پ 6 = 10 نیوتن. بارهایی که وزن آنها برابر با صفر است در نقشه نشان داده نمی شوند.

توجه داشته باشید. هنگام حل یک مشکل، استفاده کنید معادله کلی دینامیک (دالامبر - اصل لاگرانژ).

راه حل مشکل

داده شده:آر 1 = 0.2 متر، r 1 = 0.1 متر، آر 2 = 0.3 متر، r 2 = 0.15 متر, ρ 1 = 0.1 متر, ρ 2 = 0.2 متر. پ 1 = 40 نیوتن، پ 2 = 0 ، پ 3 = 0 ، پ 4 = 20 نیوتن، پ 5 = 30 نیوتن، پ 6 = 10 نیوتن، M = 10 نیوتن متر.

پیدا کردن:آ 5 .

ایجاد روابط سینماتیکی

بیایید روابط سینماتیکی برقرار کنیم. اجازه دهید V 4 ، V 5 ، V 6 ، آ 4 ، آ 5 ، آ 6 ، δS 4 ، δS 5 ، δS 6 - سرعت ها، شتاب ها و حرکات کوچک بارهای 4،5 و 6. اجازه دهید ω 1 , ω 2 , ε 1 , ε 2 , δφ 1 , δφ 2 - سرعت های زاویه ای، شتاب های زاویه ای و زوایای کوچک چرخش قرقره های 1 و 2.

سرعت حرکت نخ بین بدنه های 2، 4 و 5:
. از اینجا.
سرعت رزوه بین قرقره های 1 و 2:
. از اینجا
.
سرعت حرکت نخ بین بدنه های 1 و 6:
.

بنابراین، ما بین سرعت اجسام ارتباط پیدا کرده ایم.
;
;
.

از آنجایی که شتاب ها مشتقاتی از سرعت ها نسبت به زمان هستند،
سپس با تفکیک فرمول های قبلی با توجه به زمان، ارتباط بین شتاب ها را پیدا می کنیم:
;
;
.

از آنجایی که سرعت ها مشتقات حرکت در زمان هستند، همین ارتباط بین حرکات بی نهایت کوچک وجود دارد.
;
;
.

نیروهای خارجی فعال

بیایید نیروهای خارجی را که بر روی سیستم عمل می کنند در نظر بگیریم.
اینها نیروهای گرانش اجسام P هستند 1 = 40 نیوتن، پ 4 = 20 نیوتن، پ 5 = 30 نیوتنو پ 6 = 10 نیوتن، به سمت پایین هدایت می شود.
جفت نیرو با ممان M = 10 نیوتن متر;
نیروهای فشار محور N 1 ، ن 2 و N قرقره 1، 2 و بلوک بی وزن.
نیروهای واکنش N 4 و N 6 ، بر روی بارهای وارد شده از سطوح عمود بر این سطوح تأثیر می گذارد.

نیروهای اینرسی

این مشکل را با استفاده از معادله کلی دینامیک با استفاده از اصل دالامبر-لاگرانژ حل خواهیم کرد. این در این واقعیت نهفته است که ابتدا نیروهای اینرسی را معرفی می کنیم. پس از معرفی نیروهای اینرسی، مسئله دینامیک به مسئله ایستا تبدیل می شود. یعنی باید نیروهای اینرسی ناشناخته را پیدا کنیم تا سیستم در حالت تعادل باشد. ما این مسئله استاتیک را با استفاده از اصل d'Alembert حل می کنیم. یعنی معتقدیم نظام حرکت کوچکی کرده است. سپس در حالت تعادل، مجموع کار انجام شده توسط تمام نیروها در طول چنین حرکتی برابر با صفر است.

بنابراین، در مرحله اول ما معرفی نیروهای اینرسی. برای انجام این کار، فرض می‌کنیم که سیستم با مقداری شتاب هنوز نامشخص حرکت می‌کند. یعنی قرقره های 1 و 2 با شتاب های زاویه ای ε می چرخند 1 و ε 2 ، به ترتیب؛ بارهای 4،5 و 6 حرکت انتقالی را با شتاب های a انجام می دهند 4 ، آ 5 و الف 6 ، به ترتیب. ارتباطاتی بین این شتاب‌ها وجود دارد که قبلاً پیدا کردیم. یعنی تمام این شتاب ها را می توان از طریق یک شتاب a بیان کرد 5 . نیروهای اینرسی به گونه‌ای تعریف می‌شوند که از نظر بزرگی برابر و در جهت مخالف آن نیروها (و گشتاور نیروها) هستند که طبق قوانین دینامیک، شتاب‌های مورد انتظار را ایجاد می‌کنند (در صورت عدم وجود نیروهای دیگر).

ماژول ها (مقادیر مطلق) نیروها و گشتاورهای اینرسی را تعیین می کنیم و از طریق a بیان می کنیم 5 .
بگذارید توده های بدن باشند.
- ممان اینرسی قرقره 1.
ممان اینرسی که روی قرقره 1 عمل می کند:
.
نیروهای اینرسی وارد بر بارهای 4، 5 و 6:
;
;
.

ما نیروهای اینرسی را در نقشه ترسیم می کنیم، با توجه به اینکه جهت آنها مخالف شتاب است.

کاربرد معادله عمومی دینامیک

ما به سیستم یک جابجایی بینهایت کوچک می دهیم. اجازه دهید بار 5 با فاصله کمی δS حرکت کند 5 . سپس زاویه چرخش δφ 1 قرقره 1 و جابجایی δS 4 و δS 6 بارهای 4 و 6 با استفاده از روابط سینماتیکی ایجاد شده قبلی تعیین می شوند. از آنجایی که نخ ها غیر قابل امتداد هستند، در طول چنین حرکتی کار نمی کنند. این بدان معنی است که سیستم دارای اتصالات ایده آل است. بنابراین می توانیم معادله دینامیک عمومی را اعمال کنیم:
,
بر اساس آن مجموع کار تمام نیروهای فعال و نیروهای اینرسی در طول چنین حرکتی برابر با صفر است.

تعیین مجموع کار نیروهای فعال خارجی و نیروهای اینرسی

کاری که یک نیرو هنگام جابجایی نقطه اعمال خود با یک جابجایی کوچک انجام می دهد برابر است با حاصل ضرب اسکالر بردارها، یعنی حاصل ضرب مقادیر مطلق بردارهای F و ds توسط کسینوس زاویه بین آنها را

کار انجام شده توسط گشتاور به طور مشابه محاسبه می شود:
.

ما کار همه نیروهای فعال و نیروهای اینرسی را تعیین می کنیم. از آنجایی که مرکز محورهای قرقره های 1، 2 و بلوک بی وزن حرکت نمی کنند، نیروهای P 1 ، ن 1 ، ن 2 و N کار نمی کنند. از آنجایی که نیروهای N 4 و N 6 بر حرکات بارهای 4 و 6 عمود هستند، سپس این نیروها نیز کار نمی کنند.

ما مجموع کار انجام شده توسط نیروهای فعال باقیمانده و نیروهای اینرسی را پیدا می کنیم.

.
عبارات را جایگزین نیروهای اینرسی می کنیم و روابط سینماتیکی را اعمال می کنیم.

.
کاهش با δS 5 و تبدیل کنید.

.
مقادیر عددی را جایگزین کنید.

;
;