विद्युत प्रेरण के वेक्टर के लिए गॉस का प्रमेय। विद्युत प्रेरण वेक्टर प्रवाह

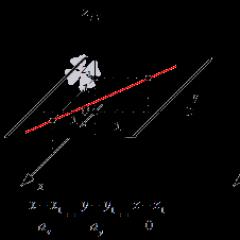
आइए हम विद्युत प्रेरण वेक्टर प्रवाह की अवधारणा का परिचय दें। आइए एक अतिसूक्ष्म क्षेत्रफल पर विचार करें। ज्यादातर मामलों में, न केवल साइट का आकार जानना आवश्यक है, बल्कि अंतरिक्ष में इसका अभिविन्यास भी जानना आवश्यक है। आइए हम सदिश-क्षेत्र की अवधारणा का परिचय दें। आइए हम सहमत हों कि क्षेत्र वेक्टर से हमारा तात्पर्य क्षेत्र के लंबवत निर्देशित और संख्यात्मक रूप से क्षेत्र के आकार के बराबर वेक्टर से है।

चित्र 1 - वेक्टर-साइट की परिभाषा की ओर

आइए वेक्टर प्रवाह को कॉल करें मंच के माध्यम से
वैक्टर का डॉट उत्पाद और
. इस प्रकार,

प्रवाह वेक्टर एक मनमानी सतह के माध्यम से सभी प्राथमिक प्रवाहों को एकीकृत करके पाया जाता है

(4)

यदि मैदान एक समान है और सतह समतल है क्षेत्र के लंबवत स्थित है, फिर:

. (5)

दी गई अभिव्यक्ति साइट को छेदने वाली बल रेखाओं की संख्या निर्धारित करती है समय की प्रति इकाई.

ओस्ट्रोग्रैडस्की-गॉस प्रमेय। विद्युत क्षेत्र शक्ति विचलन

एक मनमानी बंद सतह के माध्यम से विद्युत प्रेरण वेक्टर प्रवाह मुक्त विद्युत आवेशों के बीजगणितीय योग के बराबर , इस सतह से ढका हुआ है

(6)

अभिव्यक्ति (6) ओ-जी प्रमेय को अभिन्न रूप में दर्शाती है। प्रमेय 0-जी अभिन्न (कुल) प्रभाव से संचालित होता है, अर्थात। अगर
यह अज्ञात है कि क्या इसका मतलब अंतरिक्ष के अध्ययन किए गए हिस्से के सभी बिंदुओं पर आवेशों की अनुपस्थिति है, या इस स्थान के विभिन्न बिंदुओं पर स्थित सकारात्मक और नकारात्मक आवेशों का योग शून्य के बराबर है।

किसी दिए गए क्षेत्र में स्थित आवेशों और उनके परिमाण को खोजने के लिए, एक संबंध की आवश्यकता होती है जो विद्युत प्रेरण के वेक्टर से संबंधित हो किसी दिए गए बिंदु पर उसी बिंदु पर आवेश के साथ।

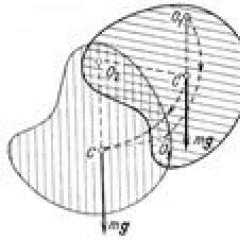
मान लीजिए हमें एक बिंदु पर आवेश की उपस्थिति निर्धारित करने की आवश्यकता है ए(अंक 2)

चित्र 2 - वेक्टर विचलन की गणना करने के लिए

आइए ओ-जी प्रमेय लागू करें। एक मनमानी सतह के माध्यम से विद्युत प्रेरण वेक्टर का प्रवाह जो उस मात्रा को सीमित करता है जिसमें बिंदु स्थित है ए, बराबर है

किसी आयतन में आवेशों का बीजगणितीय योग आयतन समाकलन के रूप में लिखा जा सकता है

(7)

कहाँ - प्रति यूनिट वॉल्यूम चार्ज करें ;

- आयतन का तत्व.

एक बिंदु पर क्षेत्र और आवेश के बीच संबंध प्राप्त करना एहम सतह को एक बिंदु तक सिकोड़कर आयतन कम कर देंगे ए. इस मामले में, हम अपनी समानता के दोनों पक्षों को मूल्य से विभाजित करते हैं . सीमा पर जाने पर, हमें मिलता है:

.

परिणामी अभिव्यक्ति का दाहिना पक्ष, परिभाषा के अनुसार, अंतरिक्ष में विचारित बिंदु पर वॉल्यूमेट्रिक चार्ज घनत्व है। बाईं ओर एक बंद सतह के माध्यम से विद्युत प्रेरण वेक्टर के प्रवाह और इस सतह से घिरे आयतन के अनुपात की सीमा का प्रतिनिधित्व करता है, जब आयतन शून्य हो जाता है। यह अदिश राशि विद्युत क्षेत्र का एक महत्वपूर्ण लक्षण है और कहलाती है वेक्टर विचलन .

इस प्रकार:

,

इस तरह

, (8)

कहाँ - वॉल्यूमेट्रिक चार्ज घनत्व।

इस संबंध का उपयोग करके, इलेक्ट्रोस्टैटिक्स की व्युत्क्रम समस्या को आसानी से हल किया जा सकता है, अर्थात। किसी ज्ञात क्षेत्र पर वितरित शुल्क ढूँढना।

यदि वेक्टर दिया गया है, जिसका अर्थ है कि इसके प्रक्षेपण ज्ञात हैं
,
,
निर्देशांक के एक फ़ंक्शन के रूप में समन्वय अक्षों पर और किसी दिए गए क्षेत्र का निर्माण करने वाले आवेशों के वितरित घनत्व की गणना करने के लिए, यह पता चलता है कि संबंधित चर के संबंध में इन अनुमानों के तीन आंशिक व्युत्पन्नों का योग ज्ञात करना पर्याप्त है। जिसके लिए उन बिंदुओं पर
कोई शुल्क नहीं। जिन बिंदुओं पर
धनात्मक, आयतन घनत्व के बराबर एक धनात्मक आवेश होता है
, और उन बिंदुओं पर जहां
एक ऋणात्मक मान होगा, एक ऋणात्मक आवेश होता है, जिसका घनत्व भी विचलन मान से निर्धारित होता है।

अभिव्यक्ति (8) प्रमेय 0-जी को विभेदक रूप में दर्शाता है। इस रूप में प्रमेय यह दर्शाता है कि विद्युत क्षेत्र के स्रोत मुक्त विद्युत आवेश हैं;विद्युत प्रेरण वेक्टर की क्षेत्र रेखाएँ क्रमशः सकारात्मक और नकारात्मक आवेशों पर शुरू और समाप्त होती हैं।

आइए विचार करें कि वेक्टर ई का मान दो मीडिया के बीच इंटरफेस पर कैसे बदलता है, उदाहरण के लिए, वायु (ε 1) और पानी (ε = 81)। पानी में क्षेत्र की ताकत अचानक 81 गुना कम हो जाती है। यह वेक्टर व्यवहार इविभिन्न वातावरणों में फ़ील्ड की गणना करते समय कुछ असुविधाएँ पैदा होती हैं। इस असुविधा से बचने के लिए, एक नया वेक्टर पेश किया गया है डी- क्षेत्र के प्रेरण या विद्युत विस्थापन का वेक्टर। वेक्टर कनेक्शन डीऔर इकी तरह लगता है

डी = ε ε 0 इ.

जाहिर है, एक बिंदु आवेश के क्षेत्र के लिए विद्युत विस्थापन बराबर होगा

यह देखना आसान है कि विद्युत विस्थापन को C/m2 में मापा जाता है, यह गुणों पर निर्भर नहीं करता है और इसे तनाव रेखाओं के समान रेखांकन द्वारा दर्शाया जाता है।

फ़ील्ड रेखाओं की दिशा अंतरिक्ष में फ़ील्ड की दिशा को दर्शाती है (फ़ील्ड लाइनें, निश्चित रूप से मौजूद नहीं हैं, उन्हें चित्रण की सुविधा के लिए पेश किया गया है) या फ़ील्ड स्ट्रेंथ वेक्टर की दिशा। तीव्रता रेखाओं का उपयोग करके, आप न केवल दिशा, बल्कि क्षेत्र की ताकत के परिमाण को भी चिह्नित कर सकते हैं। ऐसा करने के लिए, उन्हें एक निश्चित घनत्व के साथ ले जाने पर सहमति हुई, ताकि तनाव रेखाओं के लंबवत एक इकाई सतह को छेदने वाली तनाव रेखाओं की संख्या वेक्टर मापांक के समानुपाती हो। इ(चित्र 78)। फिर प्रारंभिक क्षेत्र डीएस को भेदने वाली रेखाओं की संख्या, जो सामान्य है एनवेक्टर के साथ एक कोण α बनाता है इ, E dScos α = E n dS के बराबर है,

जहाँ E n सदिश घटक है इसामान्य दिशा में एन. मान dФ E = E n dS = इडी एसबुलाया साइट के माध्यम से तनाव वेक्टर का प्रवाहडी एस(डी एस= डी.एस एन).

एक मनमाना बंद सतह S के लिए वेक्टर प्रवाह इइस सतह के माध्यम से बराबर है

एक समान अभिव्यक्ति में विद्युत विस्थापन वेक्टर Ф D का प्रवाह होता है

.

ओस्ट्रोग्रैडस्की-गॉस प्रमेय

यह प्रमेय हमें किसी भी संख्या में आवेशों से वैक्टर ई और डी के प्रवाह को निर्धारित करने की अनुमति देता है। आइए एक बिंदु आवेश Q लें और वेक्टर के प्रवाह को परिभाषित करें इत्रिज्या r की एक गोलाकार सतह के माध्यम से, जिसके केंद्र पर यह स्थित है।

एक गोलाकार सतह के लिए α = 0, cos α = 1, E n = E, S = 4 πr 2 और

Ф ई = ई · 4 πआर 2 .

E के लिए व्यंजक को प्रतिस्थापित करने पर हमें प्राप्त होता है

इस प्रकार, प्रत्येक बिंदु आवेश से F E वेक्टर का प्रवाह निकलता है इ Q/ ε 0 के बराबर। इस निष्कर्ष को बिंदु आवेशों की मनमानी संख्या के सामान्य मामले में सामान्यीकृत करते हुए, हम प्रमेय का सूत्रीकरण देते हैं: वेक्टर का कुल प्रवाह इमनमाने आकार की एक बंद सतह के माध्यम से संख्यात्मक रूप से इस सतह के अंदर निहित विद्युत आवेशों के बीजगणितीय योग के बराबर होता है, जिसे ε 0 से विभाजित किया जाता है, अर्थात।

विद्युत विस्थापन वेक्टर फ्लक्स के लिए डीआप एक समान सूत्र प्राप्त कर सकते हैं

एक बंद सतह के माध्यम से प्रेरण वेक्टर का प्रवाह इस सतह द्वारा कवर किए गए विद्युत आवेशों के बीजगणितीय योग के बराबर है।

यदि हम एक बंद सतह लेते हैं जो आवेश को ग्रहण नहीं करती है, तो प्रत्येक पंक्ति इऔर डीइस सतह को दो बार पार करेगा - प्रवेश और निकास पर, इसलिए कुल प्रवाह शून्य हो जाता है। यहां प्रवेश करने और जाने वाली रेखाओं के बीजगणितीय योग को ध्यान में रखना आवश्यक है।

विमानों, गोले और सिलेंडरों द्वारा बनाए गए विद्युत क्षेत्रों की गणना करने के लिए ओस्ट्रोग्रैडस्की-गॉस प्रमेय का अनुप्रयोग

त्रिज्या R की एक गोलाकार सतह पर Q आवेश होता है, जो सतह घनत्व σ के साथ सतह पर समान रूप से वितरित होता है

आइए गोले के बाहर केंद्र से दूरी r पर बिंदु A लें और मानसिक रूप से सममित रूप से आवेशित त्रिज्या r का एक गोला बनाएं (चित्र 79)। इसका क्षेत्रफल S = 4 πr 2 है। वेक्टर E का फ्लक्स बराबर होगा

ओस्ट्रोग्रैडस्की-गॉस प्रमेय के अनुसार
, इस तरह,
इस बात को ध्यान में रखते हुए कि Q = σ 4 πr 2, हम प्राप्त करते हैं

गोले की सतह पर स्थित बिंदुओं के लिए (R = r)

डी एक खोखले गोले के अंदर स्थित बिंदुओं के लिए (गोले के अंदर कोई चार्ज नहीं है), E = 0.

2 . त्रिज्या R और लंबाई वाली खोखली बेलनाकार सतह एलनिरंतर सतह चार्ज घनत्व के साथ चार्ज किया गया
(चित्र 80)। आइए हम त्रिज्या r > R की एक समाक्षीय बेलनाकार सतह बनाएं।

प्रवाह वेक्टर इइस सतह के माध्यम से

गॉस के प्रमेय द्वारा

उपरोक्त समानताओं के दाएँ पक्ष की बराबरी करने पर, हम प्राप्त करते हैं

.

यदि सिलेंडर (या पतले धागे) का रैखिक चार्ज घनत्व दिया गया है
वह

3. सतह आवेश घनत्व σ के साथ अनंत तलों का क्षेत्र (चित्र 81)।

आइए एक अनंत तल द्वारा निर्मित क्षेत्र पर विचार करें। समरूपता विचार से यह निष्कर्ष निकलता है कि क्षेत्र के किसी भी बिंदु पर तीव्रता की दिशा समतल के लंबवत होती है।

सममित बिंदुओं पर E परिमाण में समान और दिशा में विपरीत होगा।

आइए हम मानसिक रूप से आधार ΔS वाले एक सिलेंडर की सतह का निर्माण करें। फिर सिलेंडर के प्रत्येक आधार से एक प्रवाह निकलेगा

F E = E ΔS, और बेलनाकार सतह के माध्यम से कुल प्रवाह F E = 2E ΔS के बराबर होगा।

सतह के अंदर एक आवेश Q = σ · ΔS होता है। गॉस के प्रमेय के अनुसार, यह सत्य होना चाहिए

कहाँ

प्राप्त परिणाम चयनित सिलेंडर की ऊंचाई पर निर्भर नहीं करता है। इस प्रकार, किसी भी दूरी पर क्षेत्र की ताकत ई परिमाण में समान है।

समान सतह आवेश घनत्व σ वाले दो अलग-अलग आवेशित विमानों के लिए, सुपरपोजिशन के सिद्धांत के अनुसार, विमानों के बीच के स्थान के बाहर क्षेत्र की ताकत शून्य E = 0 है, और विमानों के बीच के स्थान में
(चित्र 82ए)। यदि समतलों पर समान सतह आवेश घनत्व वाले समान आवेशों का आवेश होता है, तो विपरीत तस्वीर देखी जाती है (चित्र 82बी)। समतलों के बीच के स्थान में E = 0, और समतलों के बाहर के स्थान में
.

विद्युत क्षेत्र शक्ति वेक्टर प्रवाह।चलो एक छोटा सा मंच डीएस(चित्र 1.2) विद्युत क्षेत्र रेखाओं को प्रतिच्छेदित करते हैं, जिनकी दिशा अभिलम्ब के साथ होती है एन इस साइट पर कोण ए. यह मानते हुए कि तनाव वेक्टर इ साइट के भीतर परिवर्तन नहीं होता डीएस, आइए परिभाषित करें तनाव वेक्टर प्रवाहमंच के माध्यम से डीएसकैसे

डीएफइ =इ डीएसओल ए.(1.3)

चूँकि विद्युत लाइनों का घनत्व तनाव के संख्यात्मक मान के बराबर होता है इ, फिर क्षेत्र को पार करने वाली विद्युत लाइनों की संख्याडीएस, संख्यात्मक रूप से प्रवाह मान के बराबर होगाडीएफइसतह के माध्यम सेडीएस. आइए हम अभिव्यक्ति के दाहिने पक्ष (1.3) को सदिशों के अदिश गुणनफल के रूप में निरूपित करें इऔरडीएस= एनडीएस, कहाँ एन- सतह पर सामान्य इकाई वेक्टरडीएस. प्रारंभिक क्षेत्र के लिए डी एसअभिव्यक्ति (1.3) रूप लेती है

डीएफइ = इडी एस

संपूर्ण साइट पर एसतनाव वेक्टर के प्रवाह की गणना सतह पर एक अभिन्न अंग के रूप में की जाती है

विद्युत प्रेरण वेक्टर प्रवाह.विद्युत प्रेरण वेक्टर का प्रवाह विद्युत क्षेत्र शक्ति वेक्टर के प्रवाह के समान ही निर्धारित होता है

डीएफडी = डीडी एस

इस तथ्य के कारण प्रवाह की परिभाषाओं में कुछ अस्पष्टता है कि प्रत्येक सतह के लिए दो हैं विपरीत दिशा में सामान्य। किसी बंद सतह के लिए, बाहरी सामान्य को सकारात्मक माना जाता है।

गॉस का प्रमेय.चलो गौर करते हैं सकारात्मक बिंदुबिजली का आवेश क्यू, एक मनमानी बंद सतह के अंदर स्थित है एस(चित्र 1.3)। सतह तत्व के माध्यम से प्रेरण वेक्टर प्रवाह डी एसके बराबर होती है
(1.4)

घटक डी एस डी = डी एस ओल एसतह तत्व डी एसप्रेरण वेक्टर की दिशा मेंडीत्रिज्या की गोलाकार सतह का एक तत्व माना जाता है आर, जिसके केंद्र में आवेश स्थित हैक्यू.

यह मानते हुए कि डी एस डी/ आर 2 बराबर है प्राथमिक शारीरिककोने डीडब्ल्यू, जिसके अंतर्गत उस बिंदु से जहां चार्ज स्थित हैक्यूसतह तत्व डी दृश्यमान एस, हम अभिव्यक्ति (1.4) को रूप में बदलते हैंडी एफडी = क्यू डी डब्ल्यू / 4 पी, जहां से, चार्ज के आसपास के पूरे स्थान पर एकीकरण के बाद, यानी 0 से 4 तक ठोस कोण के भीतरपी, हम पाते हैं

एफडी = क्यू.

मनमाने आकार की एक बंद सतह के माध्यम से विद्युत प्रेरण वेक्टर का प्रवाह इस सतह के अंदर मौजूद चार्ज के बराबर होता है.

यदि एक मनमाना बंद सतह एसएक बिंदु प्रभार को कवर नहीं करता क्यू(चित्र 1.4), फिर, उस बिंदु पर शीर्ष के साथ एक शंक्वाकार सतह का निर्माण करके जहां चार्ज स्थित है, हम सतह को विभाजित करते हैं एसदो भागों में: एस 1 और एस 2. प्रवाह वेक्टर डी सतह के माध्यम से एसहम सतहों के माध्यम से फ्लक्स के बीजगणितीय योग के रूप में पाते हैं एस 1 और एस 2:

.

दोनों सतह उस बिंदु से हैं जहां चार्ज स्थित है क्यूएक ठोस कोण से दिखाई देता है डब्ल्यू. इसलिए प्रवाह समान हैं

चूंकि एक बंद सतह के माध्यम से प्रवाह की गणना करते समय, हम इसका उपयोग करते हैं बाहरी सामान्यसतह पर, यह देखना आसान है कि प्रवाह एफ -1 डी < 0, тогда как поток Ф2डी> 0. कुल प्रवाह Ф डी= 0. इसका मतलब यह है मनमाने आकार की बंद सतह के माध्यम से विद्युत प्रेरण वेक्टर का प्रवाह इस सतह के बाहर स्थित आवेशों पर निर्भर नहीं करता है।

यदि विद्युत क्षेत्र बिंदु आवेशों की एक प्रणाली द्वारा निर्मित होता है क्यू 1 , क्यू 2 ,¼ , क्यू.एन, जो एक बंद सतह से ढका हुआ है एस, फिर, सुपरपोजिशन के सिद्धांत के अनुसार, इस सतह के माध्यम से प्रेरण वेक्टर का प्रवाह प्रत्येक चार्ज द्वारा बनाए गए फ्लक्स के योग के रूप में निर्धारित किया जाता है। मनमाना आकार की एक बंद सतह के माध्यम से विद्युत प्रेरण वेक्टर का प्रवाह इस सतह द्वारा कवर किए गए आवेशों के बीजगणितीय योग के बराबर है:

यह ध्यान दिया जाना चाहिए कि आरोप क्यू मैंबिंदु-सदृश होना आवश्यक नहीं है, एक आवश्यक शर्त यह है कि आवेशित क्षेत्र पूरी तरह से सतह से ढका होना चाहिए। यदि किसी बंद सतह से घिरे स्थान में एस, विद्युत आवेश लगातार वितरित होता है, तो यह माना जाना चाहिए कि प्रत्येक प्रारंभिक आयतन डी वीएक चार्ज है. इस मामले में, अभिव्यक्ति (1.5) के दाईं ओर, आरोपों के बीजगणितीय योग को एक बंद सतह के अंदर संलग्न मात्रा पर एकीकरण द्वारा प्रतिस्थापित किया जाता है एस:

(1.6)

अभिव्यक्ति (1.6) सबसे सामान्य सूत्रीकरण है गॉस प्रमेय: मनमाना आकार की एक बंद सतह के माध्यम से विद्युत प्रेरण वेक्टर का प्रवाह इस सतह द्वारा कवर किए गए आयतन में कुल चार्ज के बराबर है और विचाराधीन सतह के बाहर स्थित चार्ज पर निर्भर नहीं करता है. विद्युत क्षेत्र शक्ति वेक्टर के प्रवाह के लिए गॉस का प्रमेय भी लिखा जा सकता है:

.

विद्युत क्षेत्र का एक महत्वपूर्ण गुण गॉस के प्रमेय से प्राप्त होता है: बल की रेखाएँ केवल विद्युत आवेशों पर ही प्रारंभ या समाप्त होती हैं या अनंत तक जाती हैं. आइए हम एक बार फिर इस बात पर जोर दें कि, इस तथ्य के बावजूद कि विद्युत क्षेत्र की ताकत इ और विद्युत प्रेरण डी सभी आवेशों के स्थान पर, एक मनमानी बंद सतह के माध्यम से इन वैक्टरों का प्रवाह निर्भर करता है एसही निर्धारित हैं वे आवेश जो सतह के अंदर स्थित होते हैं एस.

गॉस प्रमेय का विभेदक रूप.ध्यान दें कि अभिन्न रूपगॉस का प्रमेय विद्युत क्षेत्र (आवेशों) के स्रोतों और आयतन में विद्युत क्षेत्र (तनाव या प्रेरण) की विशेषताओं के बीच संबंध को दर्शाता है वीमनमाना, लेकिन अभिन्न संबंधों के निर्माण के लिए पर्याप्त, परिमाण। आयतन को विभाजित करके वीछोटी मात्रा के लिए वी मैं, हमें अभिव्यक्ति मिलती है

संपूर्ण रूप से और प्रत्येक पद के लिए मान्य। आइए परिणामी अभिव्यक्ति को इस प्रकार रूपांतरित करें:

(1.7)

और उस सीमा पर विचार करें जहां समानता के दाईं ओर की अभिव्यक्ति, घुंघराले कोष्ठक में संलग्न, मात्रा के असीमित विभाजन की ओर प्रवृत्त होती है वी. गणित में इस सीमा को कहा जाता है विचलनवेक्टर (इस मामले में, विद्युत प्रेरण का वेक्टर डी):

वेक्टर विचलन डीकार्तीय निर्देशांक में:

इस प्रकार, अभिव्यक्ति (1.7) इस रूप में बदल जाती है:

.

यह मानते हुए कि असीमित विभाजन के साथ अंतिम अभिव्यक्ति के बाईं ओर का योग एक वॉल्यूम इंटीग्रल में चला जाता है, हम प्राप्त करते हैं

परिणामी संबंध किसी भी मनमाने ढंग से चुनी गई मात्रा के लिए संतुष्ट होना चाहिए वी. यह तभी संभव है जब अंतरिक्ष में प्रत्येक बिंदु पर समाकलन का मान समान हो। इसलिए, वेक्टर का विचलन डीसमानता द्वारा एक ही बिंदु पर आवेश घनत्व से संबंधित है

या इलेक्ट्रोस्टैटिक क्षेत्र शक्ति वेक्टर के लिए

ये समानताएँ गॉस के प्रमेय को व्यक्त करती हैं विभेदक रूप.

ध्यान दें कि गॉस प्रमेय के विभेदक रूप में संक्रमण की प्रक्रिया में, एक संबंध प्राप्त होता है जिसमें एक सामान्य चरित्र होता है:

.

अभिव्यक्ति को गॉस-ओस्ट्रोग्रैडस्की फॉर्मूला कहा जाता है और यह एक वेक्टर के विचलन के वॉल्यूम इंटीग्रल को वॉल्यूम को सीमित करने वाली एक बंद सतह के माध्यम से इस वेक्टर के प्रवाह के साथ जोड़ता है।

प्रशन

1) निर्वात में स्थिरवैद्युत क्षेत्र के लिए गॉस के प्रमेय का भौतिक अर्थ क्या है?

2) घन के केंद्र में एक बिंदु आवेश होता हैक्यू. एक वेक्टर का प्रवाह क्या है? इ:

क) घन की पूरी सतह के माध्यम से; ख) घन के किसी एक फलक से होकर।

क्या उत्तर बदल जायेंगे यदि:

a) आवेश घन के केंद्र में नहीं, बल्कि उसके अंदर होता है ; b) आवेश घन के बाहर है।

3) रैखिक, सतही, आयतन आवेश घनत्व क्या हैं?

4) आयतन और सतह आवेश घनत्व के बीच संबंध बताएं।

5) क्या विपरीत और समान रूप से आवेशित समानांतर अनंत विमानों के बाहर का क्षेत्र गैर-शून्य हो सकता है?

6) एक विद्युत द्विध्रुव को एक बंद सतह के अंदर रखा जाता है। इस सतह से प्रवाह क्या है?

विद्युत आवेशों की परस्पर क्रिया का नियम - कूलम्ब का नियम - तथाकथित गॉस प्रमेय के रूप में, अलग ढंग से तैयार किया जा सकता है। गॉस का प्रमेय कूलम्ब के नियम और सुपरपोजिशन के सिद्धांत के परिणामस्वरूप प्राप्त होता है। प्रमाण दो बिंदु आवेशों के बीच परस्पर क्रिया के बल और उनके बीच की दूरी के वर्ग के व्युत्क्रम आनुपातिकता पर आधारित है। इसलिए, गॉस का प्रमेय किसी भी भौतिक क्षेत्र पर लागू होता है जहां उलटा वर्ग कानून और सुपरपोजिशन सिद्धांत लागू होता है, उदाहरण के लिए, गुरुत्वाकर्षण क्षेत्र पर।

चावल। 9. किसी बिंदु आवेश की विद्युत क्षेत्र शक्ति की रेखाएँ एक बंद सतह X को काटती हैं

गॉस के प्रमेय को तैयार करने के लिए, आइए हम एक स्थिर बिंदु आवेश की विद्युत क्षेत्र रेखाओं के चित्र पर वापस लौटें। एकान्त बिंदु आवेश की क्षेत्र रेखाएँ सममित रूप से स्थित रेडियल सीधी रेखाएँ होती हैं (चित्र 7)। आप ऐसी कितनी भी रेखाएँ खींच सकते हैं। आइए हम उनकी कुल संख्या को आवेश से दूरी पर क्षेत्र रेखाओं के घनत्व से निरूपित करें, अर्थात, त्रिज्या के एक गोले की इकाई सतह को पार करने वाली रेखाओं की संख्या के बराबर है। इस संबंध की क्षेत्र की ताकत के लिए अभिव्यक्ति के साथ तुलना करें बिंदु आवेश (4), हम देखते हैं कि रेखाओं का घनत्व क्षेत्र की ताकत के समानुपाती होता है। हम फ़ील्ड लाइनों N की कुल संख्या को उचित रूप से चुनकर इन मात्राओं को संख्यात्मक रूप से बराबर कर सकते हैं:

इस प्रकार, एक बिंदु आवेश को घेरने वाले किसी भी त्रिज्या के गोले की सतह समान संख्या में बल रेखाओं को काटती है। इसका मतलब यह है कि बल की रेखाएं निरंतर होती हैं: विभिन्न त्रिज्याओं के किन्हीं दो संकेंद्रित क्षेत्रों के बीच के अंतराल में, कोई भी रेखा टूटी नहीं होती है और कोई नई रेखा नहीं जोड़ी जाती है। चूँकि क्षेत्र रेखाएँ सतत होती हैं, समान संख्या में क्षेत्र रेखाएँ आवेश को कवर करने वाली किसी भी बंद सतह को काटती हैं (चित्र 9)।

बल की रेखाओं की एक दिशा होती है। धनात्मक आवेश के मामले में, वे आवेश के आसपास की बंद सतह से निकलते हैं, जैसा कि चित्र में दिखाया गया है। 9. ऋणात्मक आवेश की स्थिति में ये सतह के अंदर चले जाते हैं। यदि बाहर जाने वाली रेखाओं की संख्या धनात्मक और आने वाली रेखाओं की संख्या ऋणात्मक मानी जाती है, तो सूत्र (8) में हम आवेश के मापांक के चिह्न को हटा सकते हैं और इसे इस रूप में लिख सकते हैं

तनाव का प्रवाह.आइए अब हम किसी सतह के माध्यम से क्षेत्र शक्ति वेक्टर प्रवाह की अवधारणा का परिचय दें। एक मनमाना क्षेत्र को मानसिक रूप से छोटे क्षेत्रों में विभाजित किया जा सकता है जिसमें तीव्रता परिमाण और दिशा में इतनी कम बदलती है कि इस क्षेत्र के भीतर क्षेत्र को एक समान माना जा सकता है। ऐसे प्रत्येक क्षेत्र में, बल की रेखाएँ समानांतर सीधी रेखाएँ होती हैं और उनका घनत्व स्थिर होता है।

चावल। 10. साइट के माध्यम से क्षेत्र शक्ति वेक्टर के प्रवाह का निर्धारण करना

आइए विचार करें कि बल की कितनी रेखाएं एक छोटे से क्षेत्र में प्रवेश करती हैं, सामान्य की दिशा तनाव की रेखाओं की दिशा के साथ एक कोण बनाती है (चित्र 10)। मान लीजिए कि यह बल की रेखाओं के लंबवत समतल पर एक प्रक्षेपण है। चूँकि प्रतिच्छेद करने वाली रेखाओं की संख्या समान है, और रेखाओं का घनत्व, स्वीकृत शर्त के अनुसार, क्षेत्र शक्ति के मापांक E के बराबर है, तो

मान ए साइट पर सामान्य की दिशा पर वेक्टर ई का प्रक्षेपण है

इसलिए, क्षेत्र को पार करने वाली विद्युत लाइनों की संख्या बराबर है

उत्पाद को सतह के माध्यम से क्षेत्र शक्ति प्रवाह कहा जाता है। सूत्र (10) से पता चलता है कि सतह के माध्यम से वेक्टर ई का प्रवाह इस सतह को पार करने वाली क्षेत्र रेखाओं की संख्या के बराबर है। ध्यान दें कि तीव्रता वेक्टर प्रवाह, सतह से गुजरने वाली क्षेत्र रेखाओं की संख्या की तरह, एक अदिश राशि है।

चावल। 11. साइट के माध्यम से तनाव वेक्टर ई का प्रवाह

बल की रेखाओं के सापेक्ष साइट के उन्मुखीकरण पर प्रवाह की निर्भरता चित्र में दिखाई गई है।

एक मनमानी सतह के माध्यम से क्षेत्र शक्ति प्रवाह प्राथमिक क्षेत्रों के माध्यम से प्रवाह का योग है जिसमें इस सतह को विभाजित किया जा सकता है। संबंधों (9) और (10) के आधार पर, यह कहा जा सकता है कि चार्ज को घेरने वाली किसी भी बंद सतह 2 के माध्यम से एक बिंदु आवेश की क्षेत्र शक्ति का प्रवाह (चित्र 9 देखें), से निकलने वाली क्षेत्र रेखाओं की संख्या के रूप में यह सतह बराबर है। इस मामले में, प्राथमिक क्षेत्रों की बंद सतह के सामान्य वेक्टर को बाहर की ओर निर्देशित किया जाना चाहिए। यदि सतह के अंदर आवेश ऋणात्मक है, तो क्षेत्र रेखाएँ इस सतह के अंदर प्रवेश करती हैं और आवेश से जुड़े क्षेत्र शक्ति वेक्टर का प्रवाह भी ऋणात्मक होता है।

यदि किसी बंद सतह के अंदर कई आवेश हैं, तो सुपरपोजिशन के सिद्धांत के अनुसार उनकी क्षेत्र शक्तियों का प्रवाह जुड़ जाएगा। कुल प्रवाह उसके बराबर होगा जिसे सतह के अंदर स्थित सभी आवेशों के बीजगणितीय योग के रूप में समझा जाना चाहिए।

यदि किसी बंद सतह के अंदर कोई विद्युत आवेश नहीं है या उनका बीजगणितीय योग शून्य है, तो इस सतह के माध्यम से क्षेत्र शक्ति का कुल प्रवाह शून्य है: जितनी अधिक बल रेखाएँ सतह से घिरे आयतन में प्रवेश करती हैं, उतनी ही संख्या में बाहर जाती हैं।

अब हम अंततः गॉस प्रमेय तैयार कर सकते हैं: किसी भी बंद सतह के माध्यम से निर्वात में विद्युत क्षेत्र शक्ति वेक्टर ई का प्रवाह इस सतह के अंदर स्थित कुल चार्ज के समानुपाती होता है। गणितीय रूप से, गॉस का प्रमेय उसी सूत्र (9) द्वारा व्यक्त किया जाता है, जहाँ से तात्पर्य आवेशों के बीजगणितीय योग से है। पूर्ण इलेक्ट्रोस्टैटिक में

इकाइयों की एसजीएसई प्रणाली में, गुणांक और गॉस प्रमेय को प्रपत्र में लिखा जाता है

एसआई में और एक बंद सतह के माध्यम से तनाव का प्रवाह सूत्र द्वारा व्यक्त किया जाता है

इलेक्ट्रोस्टैटिक्स में गॉस प्रमेय का व्यापक रूप से उपयोग किया जाता है। कुछ मामलों में, इसका उपयोग सममित रूप से स्थित आवेशों द्वारा बनाए गए फ़ील्ड की आसानी से गणना करने के लिए किया जा सकता है।

सममित स्रोतों के क्षेत्र.आइए हम त्रिज्या की एक गेंद की सतह पर समान रूप से चार्ज किए गए विद्युत क्षेत्र की तीव्रता की गणना करने के लिए गॉस प्रमेय को लागू करें। निश्चितता के लिए हम इसके आवेश को धनात्मक मानेंगे। क्षेत्र बनाने वाले आवेशों के वितरण में गोलाकार समरूपता होती है। इसलिए, क्षेत्र में भी समान समरूपता है। ऐसे क्षेत्र की बल रेखाएं त्रिज्या के अनुदिश निर्देशित होती हैं, और गेंद के केंद्र से समान दूरी पर सभी बिंदुओं पर तीव्रता मापांक समान होता है।

गेंद के केंद्र से कुछ दूरी पर क्षेत्र की ताकत का पता लगाने के लिए, आइए मानसिक रूप से गेंद के साथ संकेंद्रित त्रिज्या की एक गोलाकार सतह बनाएं। चूंकि इस गोले के सभी बिंदुओं पर क्षेत्र की ताकत इसकी सतह के लंबवत निर्देशित होती है और यही है निरपेक्ष मान में समान, तीव्रता का प्रवाह क्षेत्र की ताकत और गोले के सतह क्षेत्र के उत्पाद के बराबर है:

लेकिन इस मात्रा को गॉस प्रमेय का उपयोग करके भी व्यक्त किया जा सकता है। यदि हम गेंद के बाहर के क्षेत्र में रुचि रखते हैं, यानी, उदाहरण के लिए, एसआई में और, (13) से तुलना करते हुए, हम पाते हैं

एसजीएसई इकाइयों की प्रणाली में, जाहिर है,

इस प्रकार, गेंद के बाहर क्षेत्र की ताकत गेंद के केंद्र पर रखे गए बिंदु आवेश के समान होती है। यदि हम गेंद के अंदर के क्षेत्र में रुचि रखते हैं, यानी, तो चूंकि गेंद की सतह पर वितरित पूरा चार्ज उस गोले के बाहर स्थित है जिसे हमने मानसिक रूप से खींचा है। इसलिए, गेंद के अंदर कोई फ़ील्ड नहीं है:

इसी प्रकार, गॉस के प्रमेय का उपयोग करके, कोई अनंत रूप से चार्ज किए गए इलेक्ट्रोस्टैटिक क्षेत्र की गणना कर सकता है

समतल के सभी बिंदुओं पर स्थिर घनत्व वाला समतल। समरूपता के कारणों से, हम मान सकते हैं कि बल की रेखाएँ विमान के लंबवत हैं, दोनों दिशाओं में इससे निर्देशित हैं और हर जगह समान घनत्व है। दरअसल, यदि अलग-अलग बिंदुओं पर क्षेत्र रेखाओं का घनत्व अलग-अलग होता, तो एक आवेशित विमान को अपने साथ ले जाने से इन बिंदुओं पर क्षेत्र में बदलाव होता, जो सिस्टम की समरूपता का खंडन करता है - इस तरह के बदलाव से क्षेत्र में बदलाव नहीं होना चाहिए। दूसरे शब्दों में, एक अनंत समान रूप से आवेशित विमान का क्षेत्र एक समान होता है।

गॉस के प्रमेय को लागू करने के लिए एक बंद सतह के रूप में, हम निम्नानुसार निर्मित एक सिलेंडर की सतह को चुनते हैं: सिलेंडर का जनरेटर बल की रेखाओं के समानांतर होता है, और आधारों में आवेशित विमान के समानांतर क्षेत्र होते हैं और इसके विपरीत पक्षों पर स्थित होते हैं (चित्र 12)। पार्श्व सतह के माध्यम से क्षेत्र शक्ति का प्रवाह शून्य है, इसलिए बंद सतह के माध्यम से कुल प्रवाह सिलेंडर के आधारों के माध्यम से प्रवाह के योग के बराबर है:

चावल। 12. एक समान रूप से आवेशित विमान की क्षेत्र शक्ति की गणना के लिए

गॉस के प्रमेय के अनुसार, समान प्रवाह विमान के उस हिस्से के आवेश से निर्धारित होता है जो सिलेंडर के अंदर होता है, और एसआई में यह फ्लक्स के लिए इन अभिव्यक्तियों की तुलना करने के बराबर है, हम पाते हैं

एसजीएसई प्रणाली में, एक समान रूप से चार्ज किए गए अनंत विमान की क्षेत्र शक्ति सूत्र द्वारा दी जाती है

परिमित आयामों की एक समान रूप से चार्ज की गई प्लेट के लिए, प्राप्त अभिव्यक्तियाँ प्लेट के किनारों से पर्याप्त दूर स्थित क्षेत्र में लगभग मान्य होती हैं और इसकी सतह से बहुत दूर नहीं होती हैं। प्लेट के किनारों के पास, क्षेत्र अब एक समान नहीं रहेगा और इसकी क्षेत्र रेखाएँ मुड़ी हुई होंगी। प्लेट के आकार की तुलना में बहुत बड़ी दूरी पर, क्षेत्र दूरी के साथ उसी तरह घटता जाता है जैसे किसी बिंदु आवेश का क्षेत्र।

सममित रूप से वितरित स्रोतों द्वारा बनाए गए क्षेत्रों के अन्य उदाहरणों में एक अनंत आयताकार धागे की लंबाई के साथ समान रूप से चार्ज किए गए क्षेत्र का क्षेत्र, एक समान रूप से चार्ज किए गए अनंत गोलाकार सिलेंडर का क्षेत्र, एक गेंद का क्षेत्र शामिल है।

संपूर्ण आयतन में समान रूप से आवेशित होना आदि। गॉस का प्रमेय इन सभी मामलों में क्षेत्र की ताकत की आसानी से गणना करना संभव बनाता है।

गॉस का प्रमेय क्षेत्र और उसके स्रोतों के बीच एक संबंध देता है, कुछ अर्थों में कूलम्ब के नियम द्वारा दिए गए संबंध के विपरीत, जो किसी को दिए गए आवेशों से विद्युत क्षेत्र निर्धारित करने की अनुमति देता है। गॉस प्रमेय का उपयोग करके, आप अंतरिक्ष के किसी भी क्षेत्र में कुल चार्ज निर्धारित कर सकते हैं जिसमें विद्युत क्षेत्र का वितरण ज्ञात है।

विद्युत आवेशों की परस्पर क्रिया का वर्णन करते समय लंबी दूरी और छोटी दूरी की कार्रवाई की अवधारणाओं के बीच क्या अंतर है? इन अवधारणाओं को गुरुत्वाकर्षण संबंधी अंतःक्रियाओं पर किस हद तक लागू किया जा सकता है?

विद्युत क्षेत्र की ताकत क्या है? जब इसे विद्युत क्षेत्र की बल विशेषता कहा जाता है तो उनका क्या मतलब है?

कोई फ़ील्ड रेखाओं के पैटर्न से किसी निश्चित बिंदु पर फ़ील्ड ताकत की दिशा और परिमाण का आकलन कैसे कर सकता है?

क्या विद्युत क्षेत्र रेखाएँ प्रतिच्छेद कर सकती हैं? अपने उत्तर के कारण बताएं।

दो आवेशों की स्थिरवैद्युत क्षेत्र रेखाओं का गुणात्मक चित्र इस प्रकार खींचिए।

एक बंद सतह के माध्यम से विद्युत क्षेत्र की ताकत का प्रवाह जीएसई और एसआई इकाइयों में विभिन्न सूत्रों (11) और (12) द्वारा व्यक्त किया जाता है। इसे प्रवाह के ज्यामितीय अर्थ के साथ कैसे समेटा जा सकता है, जो सतह को पार करने वाली बल रेखाओं की संख्या से निर्धारित होता है?

जब इसे बनाने वाले आवेश सममित रूप से वितरित होते हैं तो विद्युत क्षेत्र की ताकत का पता लगाने के लिए गॉस के प्रमेय का उपयोग कैसे करें?

ऋणात्मक आवेश वाली गेंद की क्षेत्र शक्ति की गणना के लिए सूत्र (14) और (15) कैसे लागू करें?

गॉस का प्रमेय और भौतिक स्थान की ज्यामिति।आइए गॉस के प्रमेय के प्रमाण को थोड़े अलग दृष्टिकोण से देखें। आइए हम सूत्र (7) पर लौटते हैं, जिससे यह निष्कर्ष निकाला गया कि समान संख्या में बल रेखाएं किसी आवेश के आसपास की किसी भी गोलाकार सतह से होकर गुजरती हैं। यह निष्कर्ष इस तथ्य के कारण है कि समानता के दोनों पक्षों के हरों में कमी आई है।

दाईं ओर यह इस तथ्य के कारण उत्पन्न हुआ कि कूलम्ब के नियम द्वारा वर्णित आवेशों के बीच परस्पर क्रिया का बल, आवेशों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। बाईं ओर, उपस्थिति ज्यामिति से संबंधित है: एक गोले का सतह क्षेत्र उसकी त्रिज्या के वर्ग के समानुपाती होता है।

रैखिक आयामों के वर्ग के सतह क्षेत्र की आनुपातिकता त्रि-आयामी अंतरिक्ष में यूक्लिडियन ज्यामिति की एक पहचान है। वास्तव में, क्षेत्रों की आनुपातिकता बिल्कुल रैखिक आयामों के वर्गों तक होती है, न कि किसी अन्य पूर्णांक डिग्री तक, अंतरिक्ष की विशेषता है

तीन आयाम। तथ्य यह है कि यह घातांक बिल्कुल दो के बराबर है, और दो से भिन्न नहीं है, यहां तक ​​​​कि नगण्य रूप से छोटी राशि से भी, यह इंगित करता है कि यह त्रि-आयामी स्थान घुमावदार नहीं है, यानी, इसकी ज्यामिति बिल्कुल यूक्लिडियन है।

इस प्रकार, गॉस का प्रमेय विद्युत आवेशों की परस्पर क्रिया के मूलभूत नियम में भौतिक स्थान के गुणों की अभिव्यक्ति है।

भौतिकी के मूलभूत नियमों और अंतरिक्ष के गुणों के बीच घनिष्ठ संबंध का विचार इन कानूनों के स्थापित होने से बहुत पहले कई उत्कृष्ट दिमागों द्वारा व्यक्त किया गया था। इस प्रकार, आई. कांट ने, कूलम्ब के नियम की खोज से तीन दशक पहले, अंतरिक्ष के गुणों के बारे में लिखा था: "त्रि-आयामीता, जाहिरा तौर पर होती है, क्योंकि मौजूदा दुनिया में पदार्थ एक दूसरे पर इस तरह से कार्य करते हैं कि कार्रवाई की शक्ति होती है दूरी के वर्ग के व्युत्क्रमानुपाती।”

कूलम्ब का नियम और गॉस का प्रमेय वास्तव में प्रकृति के एक ही नियम को अलग-अलग रूपों में व्यक्त करते हैं। कूलम्ब का नियम लंबी दूरी की कार्रवाई की अवधारणा को दर्शाता है, जबकि गॉस का प्रमेय अंतरिक्ष को भरने वाले बल क्षेत्र के विचार से आता है, यानी, छोटी दूरी की कार्रवाई की अवधारणा से। इलेक्ट्रोस्टैटिक्स में, बल क्षेत्र का स्रोत एक चार्ज है, और स्रोत से जुड़े क्षेत्र की विशेषता - तीव्रता का प्रवाह - खाली स्थान में नहीं बदल सकता है जहां कोई अन्य चार्ज नहीं है। चूँकि प्रवाह को क्षेत्र रेखाओं के एक समूह के रूप में कल्पना की जा सकती है, प्रवाह की अपरिवर्तनीयता इन रेखाओं की निरंतरता में प्रकट होती है।

गॉस का प्रमेय, दूरी के वर्ग के साथ अंतःक्रिया की व्युत्क्रम आनुपातिकता और सुपरपोजिशन (अंतःक्रिया की योगात्मकता) के सिद्धांत पर आधारित, किसी भी भौतिक क्षेत्र पर लागू होता है जिसमें व्युत्क्रम वर्ग नियम लागू होता है। विशेष रूप से, यह गुरुत्वाकर्षण क्षेत्र के लिए भी सत्य है। यह स्पष्ट है कि यह महज एक संयोग नहीं है, बल्कि इस तथ्य का प्रतिबिंब है कि त्रि-आयामी यूक्लिडियन भौतिक अंतरिक्ष में विद्युत और गुरुत्वाकर्षण दोनों परस्पर क्रियाएं चलती हैं।

गॉस प्रमेय विद्युत आवेशों की परस्पर क्रिया के नियम की किस विशेषता पर आधारित है?

गॉस प्रमेय के आधार पर सिद्ध करें कि किसी बिंदु आवेश की विद्युत क्षेत्र शक्ति दूरी के वर्ग के व्युत्क्रमानुपाती होती है। इस प्रमाण में अंतरिक्ष समरूपता के किन गुणों का उपयोग किया जाता है?

कूलम्ब के नियम और गॉस के प्रमेय में भौतिक स्थान की ज्यामिति किस प्रकार परिलक्षित होती है? इन कानूनों की कौन सी विशेषता ज्यामिति की यूक्लिडियन प्रकृति और भौतिक स्थान की त्रि-आयामीता को इंगित करती है?

सामान्य सूत्रीकरण: किसी भी मनमाने ढंग से चुनी गई बंद सतह के माध्यम से विद्युत क्षेत्र शक्ति वेक्टर का प्रवाह इस सतह के अंदर मौजूद विद्युत आवेश के समानुपाती होता है।

एसजीएसई प्रणाली में:

एसआई प्रणाली में:

एक बंद सतह के माध्यम से विद्युत क्षेत्र शक्ति वेक्टर का प्रवाह है।

- आयतन में निहित कुल आवेश जो सतह को सीमित करता है।

- विद्युत स्थिरांक.

यह अभिव्यक्ति गॉस के प्रमेय को अभिन्न रूप में दर्शाती है।

विभेदक रूप में, गॉस का प्रमेय मैक्सवेल के समीकरणों में से एक से मेल खाता है और इसे निम्नानुसार व्यक्त किया गया है

एसआई प्रणाली में:

,

एसजीएसई प्रणाली में:

यहां वॉल्यूमेट्रिक चार्ज घनत्व (एक माध्यम की उपस्थिति के मामले में, मुक्त और बाध्य चार्ज की कुल घनत्व) है, और नाबला ऑपरेटर है।

गॉस के प्रमेय के लिए, सुपरपोजिशन का सिद्धांत मान्य है, अर्थात सतह के माध्यम से तीव्रता वेक्टर का प्रवाह सतह के अंदर चार्ज वितरण पर निर्भर नहीं करता है।

गॉस के प्रमेय का भौतिक आधार कूलम्ब का नियम है या, दूसरे शब्दों में, गॉस का प्रमेय कूलम्ब के नियम का एक अभिन्न सूत्रीकरण है।

विद्युत प्रेरण (विद्युत विस्थापन) के लिए गॉस का प्रमेय।

पदार्थ के किसी क्षेत्र के लिए, गॉस के इलेक्ट्रोस्टैटिक प्रमेय को अलग तरीके से लिखा जा सकता है - विद्युत विस्थापन वेक्टर (विद्युत प्रेरण) के प्रवाह के माध्यम से। इस मामले में, प्रमेय का सूत्रीकरण इस प्रकार है: एक बंद सतह के माध्यम से विद्युत विस्थापन वेक्टर का प्रवाह इस सतह के अंदर निहित मुक्त विद्युत आवेश के समानुपाती होता है:

यदि हम किसी पदार्थ में क्षेत्र की ताकत के लिए प्रमेय पर विचार करते हैं, तो चार्ज क्यू के रूप में सतह के अंदर स्थित मुक्त चार्ज और ढांकता हुआ के ध्रुवीकरण (प्रेरित, बाध्य) चार्ज का योग लेना आवश्यक है:

,

कहाँ ,
ढांकता हुआ का ध्रुवीकरण वेक्टर है।

चुंबकीय प्रेरण के लिए गॉस का प्रमेय

किसी भी बंद सतह के माध्यम से चुंबकीय प्रेरण वेक्टर का प्रवाह शून्य है:

.

यह इस तथ्य के समतुल्य है कि प्रकृति में कोई "चुंबकीय आवेश" (मोनोपोल) नहीं हैं जो एक चुंबकीय क्षेत्र बनाते हैं, जैसे विद्युत आवेश एक विद्युत क्षेत्र बनाते हैं। दूसरे शब्दों में, चुंबकीय प्रेरण के लिए गॉस का प्रमेय दर्शाता है कि चुंबकीय क्षेत्र भंवर है।

गॉस प्रमेय का अनुप्रयोग

विद्युत चुम्बकीय क्षेत्र की गणना के लिए निम्नलिखित मात्राओं का उपयोग किया जाता है:

वॉल्यूमेट्रिक चार्ज घनत्व (ऊपर देखें)।

सतह चार्ज घनत्व

जहाँ dS एक अतिसूक्ष्म सतह क्षेत्र है।

रैखिक आवेश घनत्व

जहाँ dl एक अतिसूक्ष्म खंड की लंबाई है।

आइए एक अनंत एकसमान आवेशित विमान द्वारा निर्मित क्षेत्र पर विचार करें। मान लीजिए कि समतल का सतह आवेश घनत्व समान और σ के बराबर है। आइए हम विमान के लंबवत जनरेटर वाले एक सिलेंडर की कल्पना करें और एक आधार ΔS विमान के सममित रूप से सापेक्ष स्थित है। समरूपता के कारण. तनाव वेक्टर का प्रवाह बराबर है। गॉस के प्रमेय को लागू करने पर, हमें मिलता है:

,

किस से

एसएसएसई प्रणाली में

यह ध्यान रखना महत्वपूर्ण है कि इसकी सार्वभौमिकता और व्यापकता के बावजूद, अभिन्न रूप में गॉस के प्रमेय का अभिन्न की गणना की असुविधा के कारण अपेक्षाकृत सीमित अनुप्रयोग है। हालाँकि, एक सममित समस्या के मामले में, इसका समाधान सुपरपोज़िशन सिद्धांत का उपयोग करने की तुलना में बहुत सरल हो जाता है।