Теорема о неравенстве сторон треугольника. Неравенство треугольника. Полные уроки — Гипермаркет знаний
- Неравенство треугольника.
Цели урока
- Познакомиться с новыми определениями и теоремами связанными с треугольниками.
- Научиться применять свойства фигур при решении задач.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить умение учащихся решать задачи.
План урока
- Из истории математики.
- Повторение ранее изученного материала.
- Изучение нового материала.
- Пример решения задачи.
- Задачи для самостоятельной проверки.
Из истории математики
Занимает почётное место в вавилонской геометрии, упоминание о нём часто встречается в папирусе Ахмеса.
Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем либо, стягивающая. Слово берёт начало от образа древнеегипетских арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова «катетос », которое означало отвес, перпендикуляр . В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века.
Евклид употребляет выражения:
«стороны, заключающие прямой угол», - для катетов;
«сторона, стягивающая прямой угол», - для гипотенузы.
Для начала в теме о неравенстве треугольника предлагаю вспомнить то что уже проходили, освежить в памяти уже изученное, а именно признаки равенства треугольников . Начнем пожалуй с исторической справки о признаках равенства треугольников. Что бы полностью разобраться в теме, что и как, когда и кем было написано и доказано.
Историческая справка о признаках равенства треугольников
Если мы обратимся к истории, то в самом первом учебнике по геометрии – «Началах» Евклида можно найти следующее определение: «Фигуры, совмещающиеся друг с другом равны между собой…». Прошло более двух тысяч лет, а определение не изменилось. Это определение о равенстве фигур можно отнести и к треугольникам.
- Итак, какие треугольники называются равными?
- Но всегда ли нам удаётся реально совместить треугольники?
- Действительно, иногда совместить треугольники нет возможности. Что же делать? Достаточно сравнить лишь три элемента одного треугольника с тремя элементами другого треугольника. Вот тут нам на помощь придут признаки равенства треугольников, они нам расскажут, какие именно элементы нужно сравнивать. Что такое признак равенства треугольников и сколько существует признаков? Некоторые условия, при которых два данных треугольника оказываются равными, называются признаками равенства треугольников. Можно сказать, что признак – это примета, по которой можно узнать те или иные свойства фигур.
Видеоурок «Неравенство треугольника» раскрывает содержание и доказательство теоремы о неравенстве треугольника. Задача данного видеоурока - облегчить запоминание теоремы и следствия из нее, понимание и запоминание хода рассуждений при ее доказательстве.
Высокий уровень наглядности материала, голосовое сопровождение дает возможность использовать данное пособие в качестве самостоятельной части урока, освобождая время учителя для улучшения качества обучения, усиления индивидуальной работы с учениками.
Видеоурок начинается с представления темы и формулировки теоремы о неравенстве треугольника. Для запоминания утверждения теоремы она выведена на экран и выделена цветом. Данная теорема утверждает, что любая сторона треугольника является меньшей суммы двух других его сторон. Доказательство утверждения предлагается рассмотреть на примере треугольника Δ, демонстрируемого под текстом теоремы на экране.
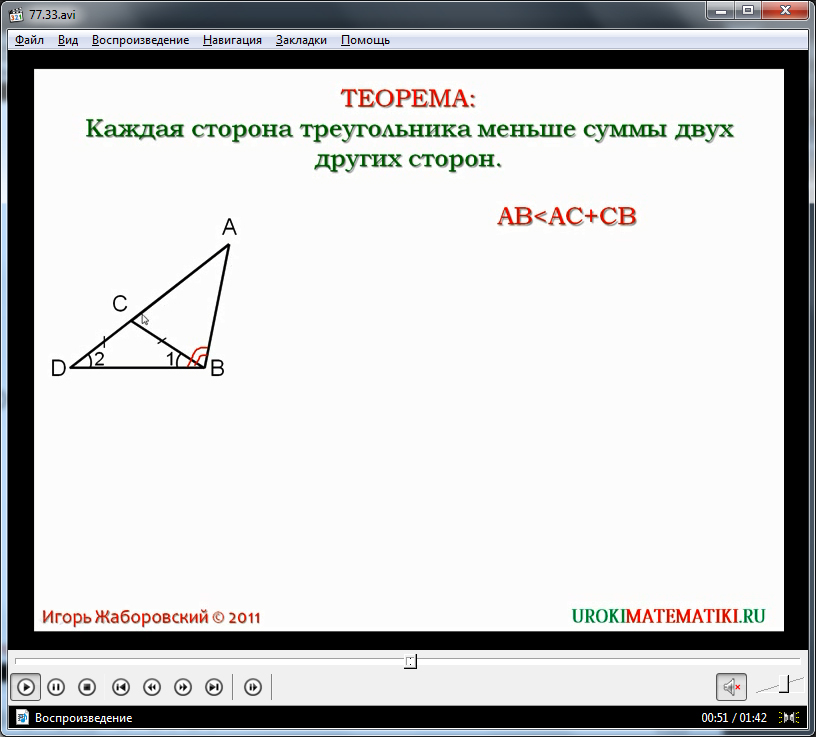
Уточняется, что для доказательства теоремы необходимо подтвердить, что сторона AB является меньше величины суммы сторон AC и CB. Данное утверждения обозначено на экране выражением AB Освоив данную теорему, можно рассматривать ее следствие, утверждающее, что для любых трех точек A,B,C, которые не принадлежат одной прямой, справедливы неравенства: AB Видеоурок «Неравенство треугольника» может быть использовано учителем на уроке геометрии в качестве наглядного пособия или как часть урока вместо объяснения учителем новой темы. Подробное понятное объяснение заменит учителя при самостоятельном изучении предмета учеником, а также поможет объяснить предмет при дистанционном обучении. Математический кружок Русановского лицея Неравенство треугольника
Неравенство треугольника – один из важнейших геометрических фактов. Представляя собой одно из интуитивных свойств расстояния, оно нередко помогает в решении непростых геометрических и текстовых задач. С помощью неравенства треугольника представляется возможным отсеять часть из возможных вариантов расположения каких-либо элементов в громоздких геометрических задачах. Часто именно невыполнение строгого неравенства треугольника (а именно – достижение в нем равенства) дает основание утверждать о принадлежности трех точек одной прямой. Таким образом, неравенство треугольника является одновременно интуитивно понятным, даже очевидным, но весьма часто становится мощным инструментом при решении серьезных математических задач. Несколько слов о неравенствах
В математике неравенство
есть утверждение об относительной величине или порядке двух рассматриваемых объектов или о том, что они просто не одинаковы. Классическое неравенство как объект исследования можно также рассматривать как частный случай отношения порядка. Различают строгие
и нестрогие
неравенства. Или же, переходя на язык отношений, строгое неравенство можно считать отношением строгого порядка на множестве действительных чисел (то есть отношением, которое обладает свойствами антирефлексивности, антисимметричности и транзитивности). Если же речь идет о нестрогом неравенстве, то можно говорить о нем как об отношении нестрогого порядка на том же множестве (то есть рассматривать вместо антирефлексивности рефлексивность). Напомним, что об отношениях как математическом объекте и их свойствах мы уже упоминали в Лекции 7 (были рассмотрены свойства отношения делимости). Более подробное их изучение нам предстоит в будущем, поскольку они довольно успешно систематизируют и обобщают ряд элементарных математических понятий. Теперь же мы приведем несколько примеров неравенств каждого из названных типов. Строгими
неравенствами называют такие неравенства: Неравенство треугольника
AO
+ OB
> AB
; CO
+ OD
> CD
. Рассмотрим сумму AC
+ BD
: AC
+ BD
= (AO
+ OC
) + (BO
+ OD
) = = (AO
+ BO
) + (OC
+ OD
) > AB
+ CD
. Аналогично: Складывая все три неравенства, получим требуемое. Упражнение
. Докажите, что медиана AM
в произвольном треугольнике ABC
по длине меньше, чем Второй же самолет пролетит расстояние Рассмотрим разность между расстоянием, которое пролетел первый самолет, и расстоянием, которое преодолел второй. Докажем, что независимо от расположения точек A
, B
, C
, D
на плоскости (городов A
, B
, C
, D
в стране) выражение будет неположительным. Для этого следует рассмотреть два случая. 1. Предположим, что точки A
, B
, C
, D
ABCD
с диагоналями AC
и BD
. Тогда запишем последовательно неравенства треугольника для треугольников ABC
, BCD
, CDA
и DAB
(см. рис. 2): AB
+ BC
> AC
; BC
+ CD
> BD
; CD
+ DA
> CA
; DA
+ AB
> DB
. Сложив все четыре неравенства, получим 2. Рассмотрим случай, когда точки A
, B
, C
, D
создают на плоскости четырехугольник A
C
BD
с диагоналями AB
и CD
(нарисуйте себе соответствующий рисунок). Заметим, что неравенства треугольника выполняются для тех же треугольников, что и в первом случае. Оказывается, что решение задачи останется тем же, несмотря на то, что расположение точек на плоскости существенно изменилось. Это можно считать еще одной характерной чертой многих решений задач, использующих неравенство треугольника. Следовательно, первый самолет прилетит раньше, поскольку его маршрут короче маршрута второго. Заметьте, что решение Задачи 5 требует небольшого анализа, что является непременным качеством всех олимпиадных задач. Будьте внимательны – Ваше решение задачи будет правильным лишь тогда, когда Вы рассмотрите все возможные случаи, подходящие под условие. Следует также отметить, что зачастую на рисунке, изображающем условие задачи, не видно треугольника, применение неравенства треугольника для которого дало бы моментальное решение. В таком случае может помочь удачно подобранное геометрическое преобразование. Об этом мы поговорим несколько позже. Знакомство с неравенством треугольника на этом следует объявить законченным. Но новая встреча с ним уже не за горами. 7 класс Лекция 13. Неравенство треугольника Фихте Иоганн Готлиб (1762-1814) - один из виднейших представителей классической немецкой философии. В книгу вошли известные работы: «Факты сознания», «Назначение человека», «Наукоучение» и другие. Каким бы зловещим не представлялся в СМИ и литературе нынешнему и прошлому поколениям национал-социализм, он не перестает привлекать к себе внимания миллионов людей. Символ защиты и власти - ПентаграммаMarsyas Пентаграмма является одним из важнейших магических символов. Само это слово происходит от греческих слов "pente", что означает пять, и "gramma" - буква; пентаграмма - Из геометрии мы знаем, что сумма длин двух сторон треугольника не меньше длины его третьей стороны. Посмотрим, как можно выразить эту теорему алгебраически. Рассмотрим треугольник расположенный так, как показано на рис. 22. Геометрическое неравенство равносильно алгебраическому неравенству треугольника Можно ли доказать последнее неравенство, не обращаясь к геометрии? В § 8 гл. III было приведено доказательство для одномерного случая (см. теорему 2 гл. III). в котором неравенство принимает следующий вид: в этой записи оно встречается чаще, чем равносильное ему неравенство Наиболее простой способ доказательства двумерного варианта неравенства треугольника (4.50) заключается в том, чтобы доказать равносильное ему неравенство. Рис. 22. Неравенство треугольника. Для этого возведем обе части неравенства (4.50) в квадрат, при этом мы придем к неравенству равносильному (4.50). Легко видеть, что последнее неравенство в свою очередь равносильно следующему: Но это неравенство является простым следствием известного неравенства Коши [двумерный вариант, см. (4.38)] что и доказывает неравенство треугольника. Как и в одномерном случае, определение условий, при которых неравенство треугольника (4.50) обращается в равенство, не представляет особого труда. Вспомним, что в неравенстве Коши (4.52) равенство достигается тогда и только тогда, когда пропорциональны, т. е. когда Неравенство (4.51) может быть получено путем извлечения квадратного корня из обеих частей неравенства (4.52). Эта операция законна, так как имеется в виду неотрицательный квадратный корень из выражения, стоящего слева. Пусть есть отрицательный квадратный корень из выражения стоящего в правой части (4.52). В этом случае даже тогда, когда пропорциональны, в (4.51) будет иметь место строгое неравенство. Таким образом, равенство в (4.51), а следовательно, и в неравенстве треугольника (4.50) достигается тогда и только тогда, когда где неотрицательный коэффициент пропорциональности. Геометрический смысл этого условия, необходимого и достаточного для того, чтобы в формуле (4.50) имело место равенство, заключается в следующем: точки (рис. 21) должны принадлежать одной прямой, причем точки расположены по одну сторону от точки О. При треугольник превращается в отрезок прямой. Иначе говоря, точки не только лежат на одной прямой с точкой О, но и лежат на одном луче с началом О. Легко убедиться в том, что полученные здесь условия согласуются с соответствующими условиями для одномерного случая (неравенства где равенство достигается тогда и только тогда, когда числа имеют один знак. Доказательство неравенства треугольника можно обобщить, следуя по тому же пути, что и при выводе неравенства Гёльдера, а именно доказать, что неравенство имеет место для любых действительных значений причем, как и прежде, равенство достигается в том и только том случае, когда числа пропорциональны и коэффициент пропорциональности положителен. Мы вернемся к этому неравенству в гл. VI, где будет рассмотрен его геометрический смысл. Перейдем к другому доказательству неравенства треугольника, которое можно использовать также и для получения более общих результатов. Имеет место тождество Неравенство Коши в форме, использующей квадратные корни [см. (4.51)], применим по очереди к двум выражениям.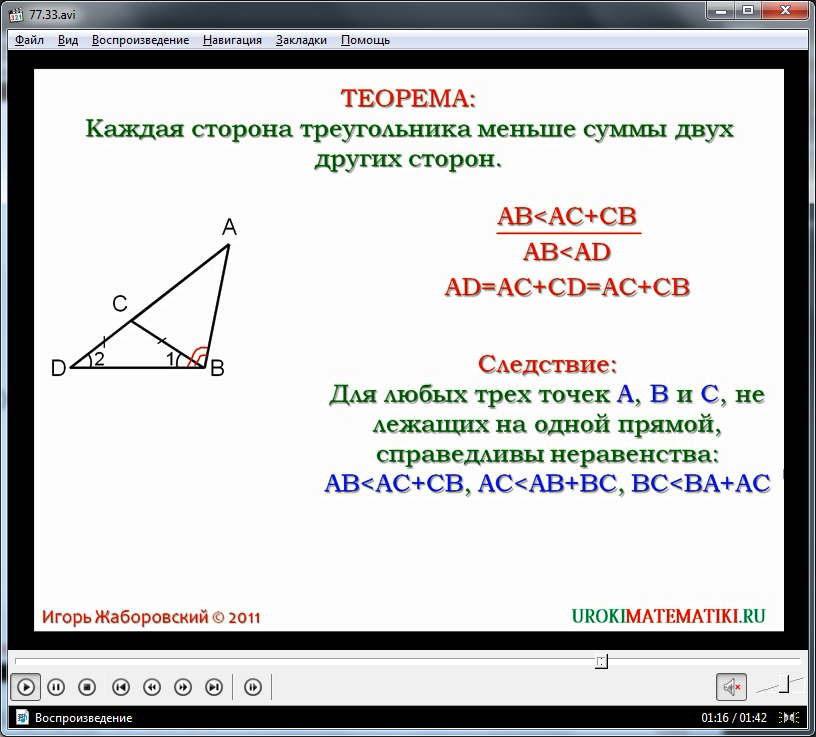
a
< b
– означает, что a
меньше
b
; a
> b
– означает, что a
больше
b
; a
≠ b
– означает, что a
не равно
b
или же что a
и b
различны
.
К нестрогим
неравенствам относят следующие математические отношения: a
≤ b
– означает, что a
меньше либо равно
b
или, что то же самое, a
не больше (не превосходит, не превышает)
b
; a
≥
b
– означает, что a
больше либо равно
b
или, что то же самое, a
не меньше
b
.
Пока что мы не будем утруждать себя более глубоким исследованием неравенств. Сегодня нам вполне хватит уже устоявшихся представлений о неравенствах.
Доказательство теоремы
. Рассмотрим треугольник ABC
и покажем, что AB
< AC
+ BC
. При доказательстве воспользуемся одним из видов дополнительных построений – откладыванием равных отрезков (метод спрямления
). В треугольнике ABC
(рис. 1) на продолжении стороны BC
отложим отрезок CD
, равный AC
. В равнобедренном треугольнике A
CD
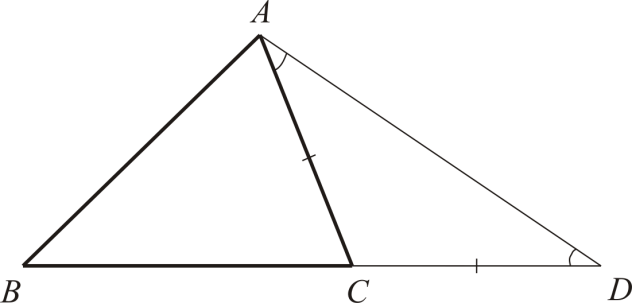
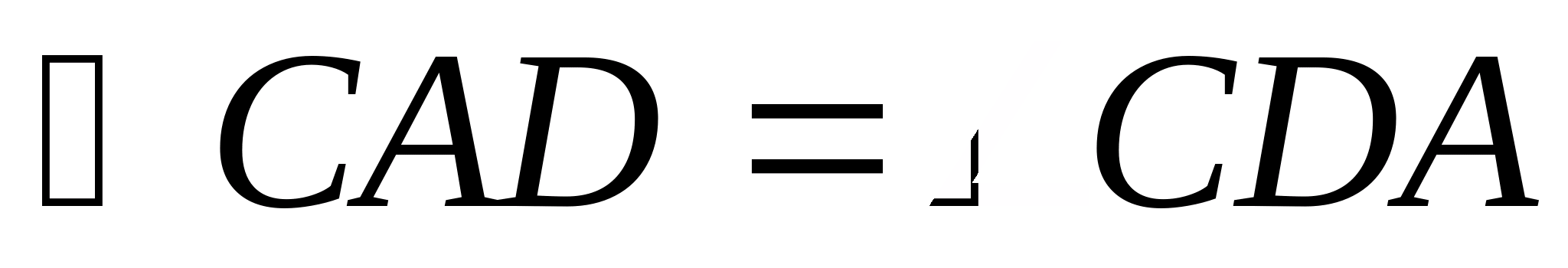. В треугольнике ABD
угол A
DB
меньше угла BAD
, значит, BD
> AB
, или BC
+ CD
> AB
. Но CD
= AC
, значит, AC
+ BC
> AB
. Замечание
. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства: AB
< AC
+ BC
; AC
< AB
+ BC
; BC
< AB
+ AC
. Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам. Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой
. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими. Упражнение
. Докажите, что в треугольнике каждая сторона больше разности двух других сторон. Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач. Задача 1
. Докажите, что в произвольном четырехугольнике ABCD
AB
+ CD
< AC
+ BD
.
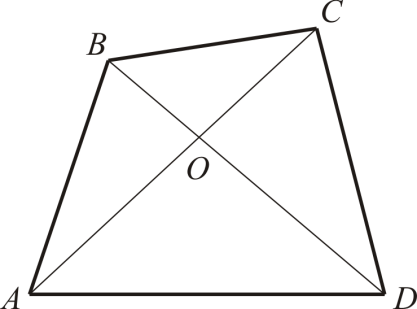
Решение
. Пусть O
– точка пересечения диагоналей четырехугольника ABCD
(рис. 2). По неравенству треугольника:
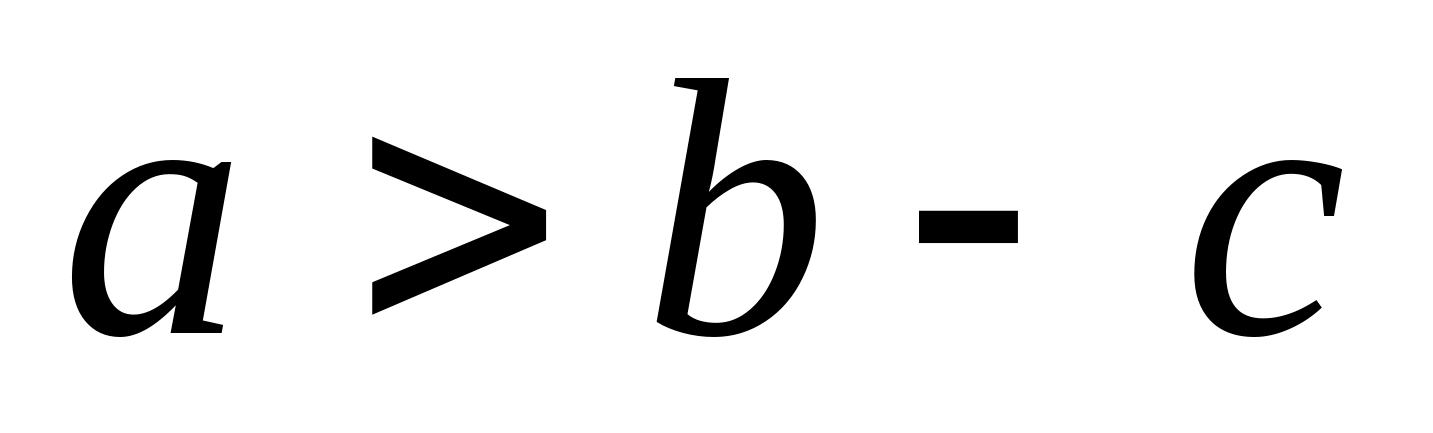(предполагаем, что 
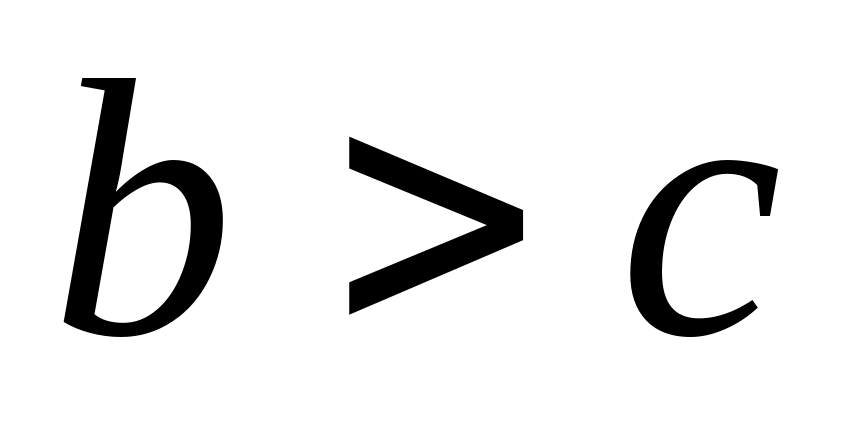). Тогда, возведя в квадрат обе части неравенства, получим: 
;
.
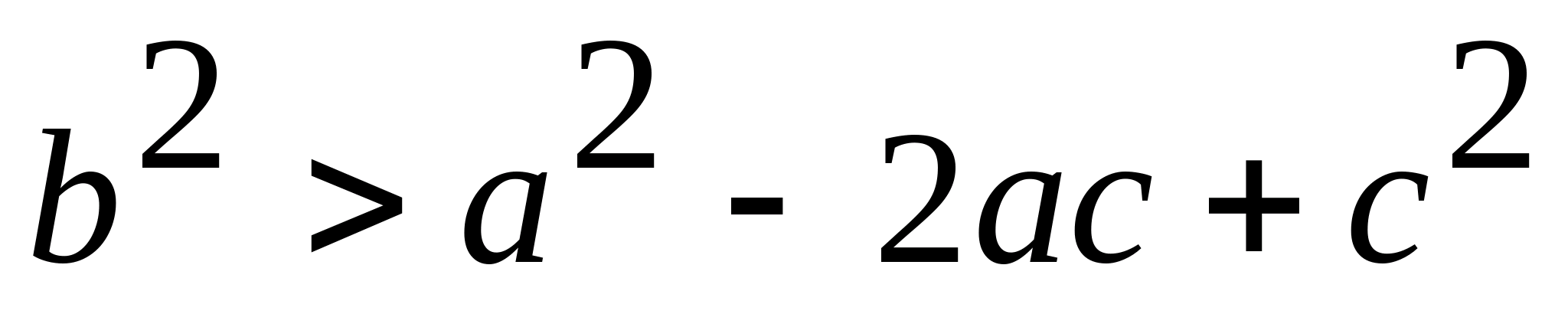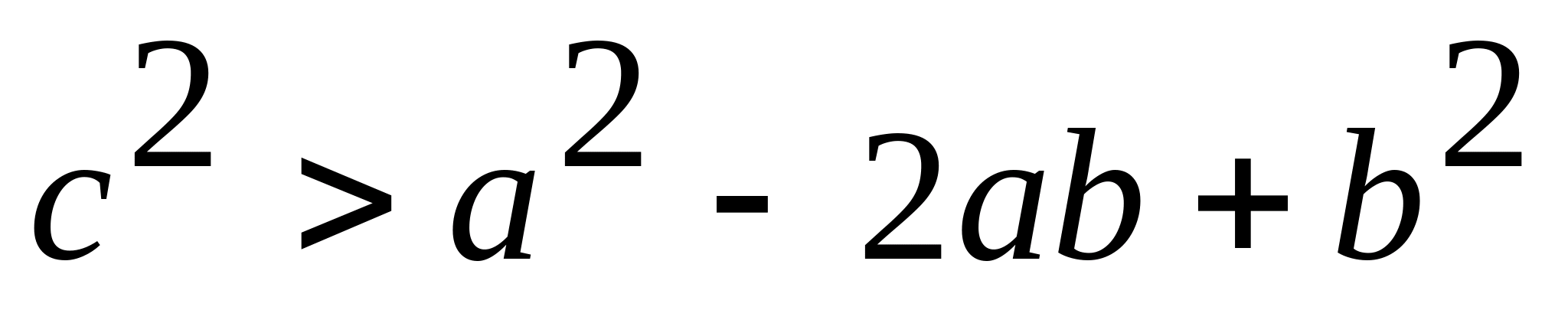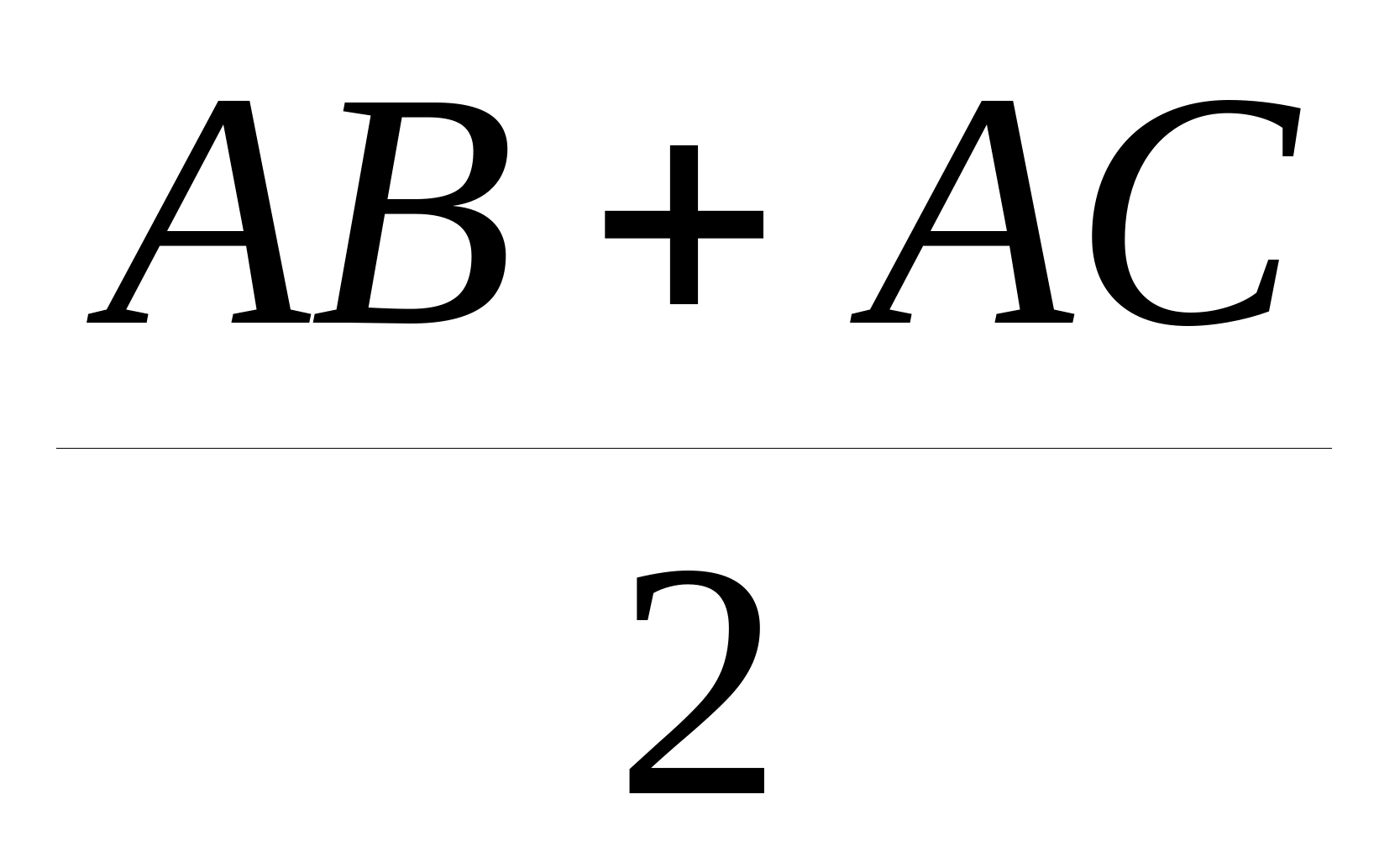. Задача 3
. На плоскости дан квадрат ABCD
и точка O
. Докажите, что расстояние от точки O
до одной из вершин квадрата не превосходит суммы расстояний от O
до трех других вершин квадрата. Решение
. Сложите неравенства треугольника AC
+ OC
> OA
и OB
+ OD
> BD
. Так как AC
= BD
, то, сокращая, получаем требуемое. Задача 4
. Найдите внутри выпуклого четырехугольника точку, такую, что сумма расстояний от нее до вершин минимальна. Решение
. Так как четырехугольник выпуклый, то его диагонали пересекаются в точке O
внутри него. Обозначим вершины четырехугольника через A
, B
, C
и D
(по часовой стрелке). Тогда сумма расстояний от O
до вершин равна сумме длин диагоналей AC
и BD
. Но для любой другой точки P
имеем, во-первых, что сумма расстояний от P
до вершин не меньше AC
+ BD
, а во-вторых, либо PA
+ PC
> AC
, либо PB
+ PD
> BD
. Значит, эта сумма равна AC
+ BD
только если P
совпадает с точкой O
. Значит, точка O
– искомая. Неравенство треугольника успешно применяется и в довольно запутанных текстовых задачах. Что интересно, в таких задачах многое может зависеть от того, насколько удачно Вы построите геометрическую интерпретацию. Задача 5
. В некоторой стране расположены 4 города: A
, B
, C
и D
. Два самолета одновременно вылетели из города A
. Маршрут первого самолета: A
-B
-D
-C
-A
-D
-B
-C
-A
, а маршрут второго: A
-B
-C
-D
-A
-B
-C
-D
-A
-B
-C
-D
-A
. Какой из самолетов раньше закончит свой маршрут, если их скорости одинаковы? Не бойтесь экспериментировать! Если в задаче не задано конкретное расположение объектов, Вы вправе рисовать в своем решении всё, что не противоречит условию – оно ведь Ваше. В том числе, и города в Задаче 5 Вы можете расставить как угодно. Следует лишь помнить, что в некоторых задачах после разбора «нормального», общего случая, необходимо разобрать и некоторые «патологические», частные случаи. К примеру, в Задаче 5 может понадобиться рассмотрение случая, когда некоторые три города лежат на одной прямой – всё зависит от того, каково Ваше решение для общего случая. Решение задачи 5
. Запишем длины маршрутов каждого из самолетов в виде сумм расстояний между городами. Длина маршрута первого самолета будет равна Фихте Иоганн Готлиб (1762-1814) один из виднейших представителей классической немецкой философии. Вкнигу вошли известные работы: «Факты сознания», «Назначение человека», «Наукоучение» идругие книга
Книга
Жозеф Артур Гобино. Опыт о неравенстве человеческих рас книга
Книга
Пентаграмма является одним из важнейших магических символов. Само это слово происходит от греческих слов "pente", что означает пять, и "gramma" буква
Документ
Загрузка...